Задача 1.
Тетраэдр в пространстве задано вершинами
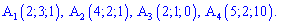
Необходимо найти:
1) уравнение грани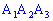 
;
2) уравнение высоты пирамиды, которая проходит через вершину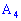 
;
3) длину этой высоты;
4) угол между ребром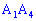 
и гранью 
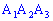в градусах;
5) площадь грани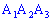
;
6) Объем пирамиды.
Решение.
1) Уравнение грани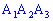 
Запишем уравнение плоскости в виде.
.
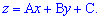Поскольку все три точки принадлежат этой плоскости, то, подставляя их по очереди получим систему уравнений
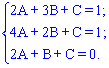
Решая ее получим.
.
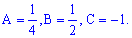Подставляя в исходное уравнение получим
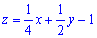, Или 
.
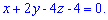2) Уравнение высоты пирамиды, проходящей через вершину 
Запишем уравнение высоты пирамиды, проходящей через вершину
.
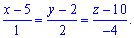3) Высота с вершины 
Найдем высоту, для этого найдем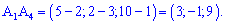 
Высоту найдем учитывая уравнение грани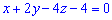 
, по формуле
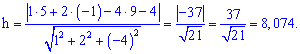
4)Угол между ребром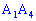 
и гранью 
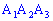в градусах
Найдем угол между ребром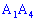 
и гранью 
(
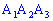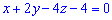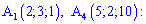
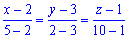) . Запишем уравнение прямой, проходящей через точки 
, или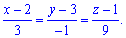 
.
Найдем синус угла по формуле
.
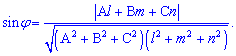Подставим значения
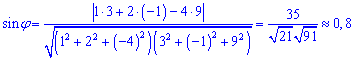
Найдем значение угла
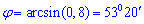
5) Площадь грани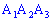 
Площадь грани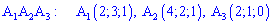
найдем по формуле
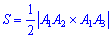
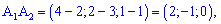
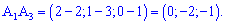
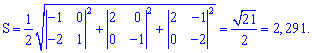
6) Объем пирамиды
Найдем объем пирамиды пирамиды по формуле
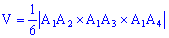, где
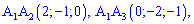
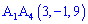
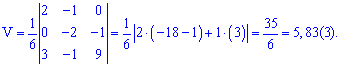
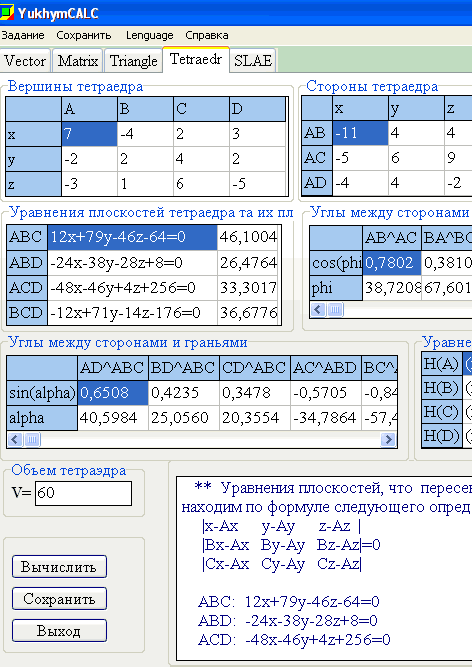
Математический калькулятор YukhymCalc решает эту задачу и немало типичных для студенческой практики математических задач. Фрагмент работы калькулятора приведены ниже.
------------------------------
Посмотреть материалы:
