Задачи на треугольник бывают простые, сложные и очень сложные. Если имеем прямоугольный треугольник то формулы для вычисления площади, катетов, радиусов вписанной и описанной окружности несколько упрощаются. Ниже приведены решения примеров на любой вкус, анализируйте их - возможно они помогут Вам в учебе.
Задача 1. Найдите синусы острых углов и гипотенузу прямоугольного треугольника если его катеты равны: а ) 6 см и 8 см; б) 4 см и 7 см.
Решение. Применим теорему Пифагора к заданным катетам
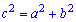
Для задания а) гипотенуза равна

та для б) соответственно
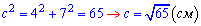
Синус острого угла в прямоугольном треугольнике равен отношению катета напротив угла к гипотенузе.
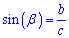
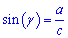 .
.
Рисунок с необходимыми формулами для синусов и формулой Пифагора приведен ниже
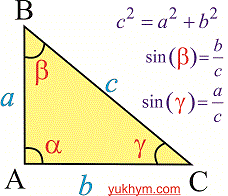
Вычисляем синусы искомых углов
а) 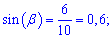
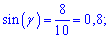
б)
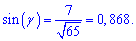
На этом пример завершен.
------------------------
Задача 2. Найдите катеты прямоугольного треугольника если его гипотенуза и второй катет соответственно равны: а ) 15 см и 9 см; б) 8 см и 4 см.
Решение. На основе теоремы Пифагора получим
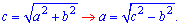
Подставляем значения
а) 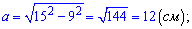
б) 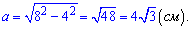
Ответ: Катеты треугольника равны 12 см и  см.
см.
------------------------
Задача 3. В прямоугольном треугольнике гипотенуза равна 17 см. Один из катетов на 7 см меньше гипотенузы. Определиите катеты треугольника.
Решение. Для заданного примера и подобных ему необходимо составлять уравнения. В этом примере обозначим через
x – большой катет. Тогда x-7 – меньший катет.
По формуле Пифагора имеем
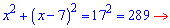
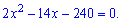
Делим на два и решаем квадратное уравнение с помощью дискриминанта
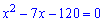
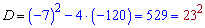
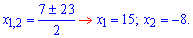
Второй корень уравнения исключаем, поскольку он противоречит условию задачи. Таким образом один катет равен 15 см, а второй – 15-7=8 см.
Ответ: Катеты прямоугольного треугольника равны 15 и 8 см.
------------------------
Задача 4. Вычислите длину высоты равностороннего треугольника сторона которого равна 12 см.
Решение. Если треугольник равносторонний то высота делит основание пополам. Кроме этого высота является перпендикуляром. Таким образом задача состоит в нахождении катета когда известно, что гипотенуза равна 12 см, а второй катет – 12/2=6 см.
По теореме Пифагора вычисляем
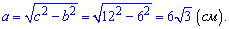
Ответ: Катет равен  см.
см.
------------------------
Задача 5. Сторона квадрата равна 7 см. Определите длину диагонали.
Решение. Поскольку стороны квадрата равны то нужно найти гипотенузу прямоугольного равнобедренного
треугольника с катетами длиной 7 см. Используем известную формулу Пифагора
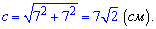
Ответ: Диагональ квадрата равна 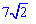 см.
см.
------------------------
Задача 6. Большая диагональ и большая основа прямоугольной трапеции равны соответственно 8 см и 6 см. Найдите длину меньшей боковой стороны трапеции.
Решение. Рассмотрим вспомогательный рисунок трапеции.
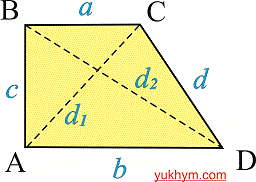
По условию известна диагональ BD=8 см и AD=6 см. Катет AB прямоугольного треугольника находим по формуле
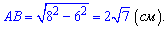
Ответ: Сторона трапеции равна 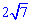 см.
см.
------------------------
Задача 7. В треугольнике АВС угол В = 90 градусов, ВD перпендикулярна АС, АВ = 16 см, ВС = 12 см. Найдите длину отрезка АD и тангенс угла при основании.
Решение. Рассмотрим вспомогательный рисунок к заданию.
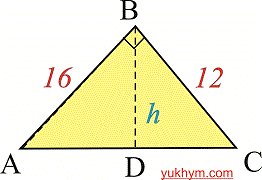
Составим пропорции для отыскания отрезка AD
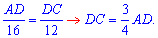
Второе уравнение построим на основе теоремы Пифагора
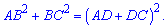
Думаю выше Вам все понятно. Следующим шагом подставляем DC и значение катетов в уравнение
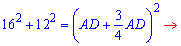
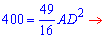
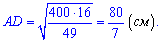
Отрезок найдено, тангенс угла А находим по формуле
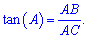
Определим длину гипотенузы - для этого найдем неизвестную часть DC
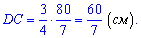
Гипотенуза равна сумме AD+DC
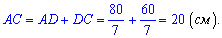
Вычислим тангенс угла при основании
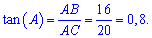
Ответ: AD=80/7, tan(A)=0,8.
------------------------
Задача 8. Периметр прямоугольного треугольника равен 12 см, а один из из его катетов - 3 см. Найдите площадь
треугольника.
Решение. Данный пример на сложение уравнения с неизвестными.
Первое уравнение соответствует формуле периметра треугольника, второе - теореме Пифагора.
Обозначим b – неизвестный катет, с – гипотенуза треугольника.
Составляем систему уравнений
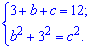
Имеем два уравнения с двумя неизвестными. Метод решения Вам известен: из первого уравнения выражаем одну из переменных и подставляем во второе. В результате после упрощений получим квадратное уравнение один из корней которого и будет решением. Второй получим в результате подстановки в первую зависимость системы уравнений.
У меня получилось что b=4 см, c=5 см.
Если не верите то можете пройти описанные выше процедуры.
Площадь находим как половину произведения катетов
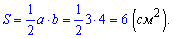
Ответ: площадь треугольника 6 сантиметров квадратных.
------------------------
Задача 9. Катеты прямоугольного треугольника равны 3 см и 4 см. Найти радиус вписанной и описанной окружности.
Решение. Радиус описанной окружности найти легче - он равен половине гипотенузы. Вычисляем ее длину по теореме Пифагора
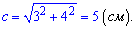
Отсюда находим больший радиус
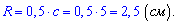
Радиус вписанной в прямоугольный треугольник окружности можно найти несколькими способами.
Пойдем простым и определим его на основе формулы площади треугольника
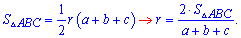
Как видите вычислить радиус вписанной окружности достаточно просто. Находим площадь треугольника
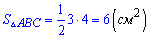
и подставляем в предыдущую формулу
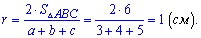
Вот такой сложный на восприятие пример легко решается при знании необходимых формул.
Ответ: радиусы описанной и вписанной окружности равны 2,5 см и 1 см соответственно.
------------------------
Изучайте формулы основных геометрических фигур, набирайтесь опыта на практике и со временем примеры будете решать без труда. Если же не удается решить пример или задачу, или непонятно условие задачи обращайтесь к специалистам. На этом сайте и подобных интернет ресурсах Вы всегда можете решить любую сложную задачу.
Посмотреть материалы

