Формул для вычисления площади треугольника в интернете можно найти свыше 10. Немало из них применяется в задачах с известными сторонами и углами треугольника. Однако есть ряд сложных примеров где по условию задания известны только одна сторона и углы треугольника, или радиус описанной или вписанной окружности и еще одна характеристика. В таких случаях простую формулу применить не удастся.
Приведенные ниже формулы позволят решить 95 процентов задач в которых требуется найти площадь треугольника.
Перейдем к рассмотрению распространенных формул площади.
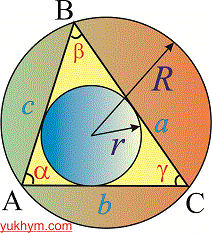
Рассмотрим треугольник изображен на рисунке ниже
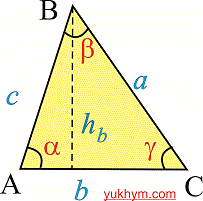
На рисунке и далее в формулах введены классические обозначения всех его характеристик
a,b,c – стороны треугольника,
R– радиус описанной окружности,
r – радиус вписанной окружности,
h[b],h[a],h[c] – высоты , проведенные в соответствии со сторонами a,b,c.
alpha, beta,hamma – углы возле вершин.
Основные формулы площади треугольника
1. Площадь равна половине произведения стороны треугольника на высоту опущенной к этой стороне. На языке формул это определение можно записать так
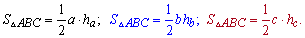
Таким образом, если известна сторона и высота - то площадь найдет каждый школьник.
Кстати, из этой формулы можно вывести одну полезную зависимость между высотами
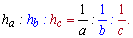
2. Если учесть, что высота треугольника через соседнюю сторону выражается зависимостью
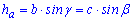
то с первой формулы площади следуют однотипные вторые
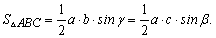
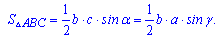
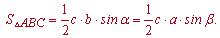
Внимательно посмотрите на формулы - их легко запомнить, поскольку в произведении фигурирует две стороны и угол между ними. Если правильно обозначить стороны и углы треугольника (как на рисунке выше) то получим две стороны a,b и угол связан с третьей С (hamma).
3. Для углов треугольника справедливо соотношение
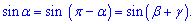
Зависимость позволяет применять в вычислениях следующие формулы площади треугольника
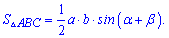
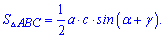
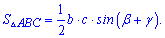
Примеры на эту зависимость встречаются крайне редко, но помнить что есть такая формула Вы должны.
4. Если известна сторона и два прилегающих угла то площадь находится по формуле
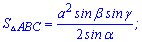
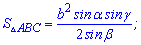
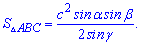
5. Формула площади через сторону и котангенс прилегающих углов следующая
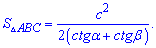
Перестановкой индексов можете получить зависимости для других сторон.
6. Приведенная ниже формула площади используется в задачах когда вершины треугольника заданы на плоскости координатами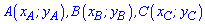 
. В этом случае площадь равна половине определителя взятого по модулю.
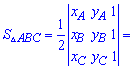
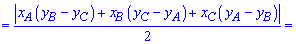
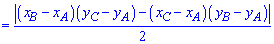
7. Формула Герона применяют в примерах с известными сторонами треугольника.
Сначала находят полупериметр треугольника
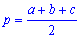
а затем определяют площадь по формуле
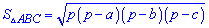
или
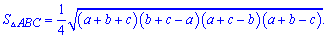
Ее довольно часто используют в коде программ калькуляторов.
8. Если известны все высоты треугольника то площадь определяют по формуле
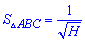
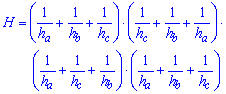
Она сложна для вычисления на калькуляторе, однако в пакетах MathCad, Mathematica, Maple площадь находится на «раз два ».
9. Следующие формулы используют известны радиусы вписанных и описанных окружностей.
В частности, если известно радиус и стороны треугольника, или его периметр то площадь вычисляется согласно формуле
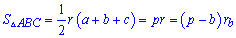
10. В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле
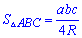
11. Следующая формула определяет площадь треугольника через сторону и углы треугольника.
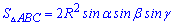
Ну и напоследок - частные случаи :
Площадь прямоугольного треугольника с катетами a и b равна половине их произведения
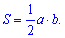
Формула площади равностороннего ( правильного ) треугольника=
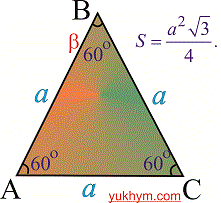
= одной четвертой произведения квадрату стороны на корень из тройки.
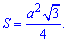
Пример. Стороны треугольника равны 3, 5, 6 см. Найти площадь треугольника.
Решение: Применим формулу Герона, для этого сначала найдем полупериметр
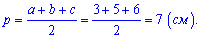
Подставляем в формулу площади
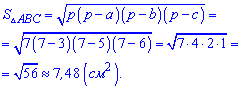
Ответ:Площадь треугольника равна 7.48 сантиметров квадратных.
------------------------------------
Скачать все приведенные формулы площади треугольника Вы можете по следующей ссылке. Распечатывайте их и используйте в обучении.
{jd_file file==19}
Если материал был полезен Вам - поделитесь ссылкой с друзьями.
Посмотреть материалы:
- Прямоугольный треугольник. Задачи
- Периметр и площадь прямоугольника
- Квадрат. Формулы
- Периметр и площадь параллелограмма
- Формулы площади трапеции
- Ромб. Площадь, периметр
{jcomments on}
