Якщо незалежна змінна одна, то рівняння називається звичайним; якщо незалежних змінних дві або більше, то рівняння називається диференціальним рівнянням з частинними похідними. З метою отримати високоваліфікованих спеціалістів у всіх ВУЗах де вивчають точні дисципліни обов'язковим є курс диференціальних рівнянь.
Для одних студентів теорія дається тяжко, практика ще з горем пополам, для інших важка і теорія, і практика. Якщо аналізувати диференціаьні рівняння з практичної сторони, то для їх обчислень Вам потрібно лише добре вміти інтегрувати та брати похідні. Все решта зводиться до кількох схем, які можливо зрозуміти та вивчити. Нижче Ви ознайомитеся з основними означеннями та першими простими диф. рівняннями.
Теорія диференціальних рівнянь
Означення: Звичайним диференціальним рівнянням називають рівняння, яке в собі зв'язує незалежну змінну х, функцію у(х) та похідні у'(х), уn(х) і має загальний вигляд F(x,y(x),y' (x), …, yn(x))=0
Диференцiальним рiвнянням (ДР) називається або звичайне диференцiальне рiвняння, або диференцiальне рiвняння з частинними похiдними.
Порядок диференціального рівняння визначається порядком старшої похідної (n), яка входить до даного диференціального рівняння.
Загальним розв'язком диференціального рівняння називається функція, яка містить стільки сталих, який порядок диференціального рівняння, і підстановка якої в дане диференціальне рівняння перетворює його в тотожність, тобто має вигляд y=f(x, C1, C2, …, Cn).
Загальний розв'язок, який не розв'язаний відносно у(х) і має вигляд F(x,y,C1,C2, …, Cn)=0 називається загальним інтегралом диференціального рівняння.
Розв'язок, знайдений із загального розвязку при фіксованих значеннях сталих C1,C2, …, Cn називається частинним розв'язком диференціального рівняння.
Одночасне задання диференціального рівняння і відповідної кількості початкових умов називається задачею Коші.
F(x,y,C1,C2, …, Cn)=0
y(x0)=y0;
….
yn(x0)=yn(0)
Звичайним диференцiальним рiвнянням першого порядку називається рiвняння вигляду
F(x, y, y')=0. (1)
Iнтегралом рiвняння (1) називається cпiввiдношення вигляду Φ(x, y)=0, якщо кожна неявно задана ним неперервно-диференцiйовна функцiя є розв'язком рiвняння (1).
Рівняння, яке має вигляд (1) і не може бути зведене до простішого вигяду називається рiвнянням, нерозв'язним стосовно похiдної. Якщо його можна записати у виглядi
y' = f(x,y), то воно називається рiвнянням, розв'язаним стосовно похiдної.
Задача Коші для рівняння першого порядку містить лише одну початкову умову і має вигляд:
F(x,y,y')=0
y(x0)=y0.
Рiвняння вигляду
M(x,y)dx+N(x,y)dx=0 (2)
де змiннi x i y є "симетричними": можна припускати, що x – незалежна, а y – залежна змiнна, або, навпаки, y – незалежна, а x – залежна змiнна, називається рiвнянням в симетричнiй формі.
Геометричний зміст диференціаьного рівняння першого порядку
y'=f(x, y) (3)
полягає в наступному.
Дане рівняння встановлює зв ' язок ( залежність ) між координатами точки (x; y) і кутовим коефіцієнтом y' дотичної до інтегральної кривої, що проходить через цю точку . Таким чином, рівняння y'=f(x, y) дає сукупність напрямів ( поле напрямів ) на декартовій площині Oxy.
Крива, побудована на точках, в яких напрям поля однаковий, називається ізокліною. Ізоклінами можна користуватися для наближеної побудови інтегральних кривих . Рівняння ізокліни можна одержати, якщо покласти похідну рівну сталій y'=С
f(x, y)=С - рівняння ізокліни.
Iнтегральною лiнiєю рiвняння (3) називається графiк розв'язку цього рiвняння.
Звичайнi диференцiальнi рiвняння, розв'язки яких можна задати аналітично y=g(x), називаються iнтегровними рiвняннями.
Рiвняння вигляду
M0(x)dx+N0(y)dy=0 (3)
називаються рiвняннями з вiдокремленними змiнними.
З них і розпочнемо знайомство з диференціальними рівняннями. Процес знаходження розв'язків диференціального рівняння ще називають інтегруванням диференціального рівняння.
Рівняння з відокремленими змінними
Приклад 1. Знайти розв'язок рівняння y'=x .
Виконати перевірку розв'язку.
Розв'язання: Запишемо рівняння в диференціалах
dy/dx=x або dy=x*dx.
Проінтегруємо праву та ліву частини рівняння
int(dy)=int(x*dx);
y=x2/2+C.
Це і є загальний інтеграл ДР.
Перевіримо його правильність, обчислимо похідну функції
y'=1/2*2x+0=x.
Як ожна переконатися, отримали вихідне ДР, отже обчислення виконані правильно.
Ми тільки що знайшли розв'язок диференціального рівняння першого порядку. Це саме простіше рівняння, яке можна собі уявити.
Приклад 2. Знайти загальний інтеграл диференціального рівняння
(x+1)y'=y+3
Розв'язання: Запишемо вихідне рівняння в диференціалах
(x+1)dy=(y+3)dx.
Отримане рівняння зводимо до ДР з відокремленими змінними
![]()
Все що залишилося це взяти інтеграл від обох частин
![]()
За табличними формулами отримаємо
ln|y+3|=ln|x+1|+C.
Якщо експонувати обидві частини, то отримаємо
y+3=e ln|x+1|+C або y=e ln|x+1|+C-3.
Такий запис є правильним, але не є компактним.
На практиці застосовують інший прийом, при обчисленні інтегралу сталу вносять під логарифм
ln|y+3|=ln|x+1|+ln(C).
За властивостями логарифма це дозволяє згорнути два останні доданки
ln|y+3|=ln(С|x+1|).
Тепер при експонуванні розв'язок диференціального рівняння матиме набагато красивіший і читабельний вигляд
y= С|x+1|+3
Запам'ятайте дане правило, на практиці воно застосовується як еталон обчислень.
Приклад 3. Розв'язати диференціальне рівняння
y'=-y*sin(x).
Розв'язання:Запишемо рівняння в диференціалах
dy/dx= y*sin(x)
або після перегрупування множників у вигляді рівняння з відокремленими змінними
dy/ y=-sin(x)dx.
Залишилося проінтегрувати праву та ліву частини рівняння
int(1/y,y)=-int(sin(x), x);
ln|y|=cos(x)-ln(C).
Константу зручно внести під логарифм, та ще й з від'ємним значенням, щоб перенісши в ліву частину отримати
ln|С*y|=cos(x).
Експонуємо обидві частини залежності
С*y=exp(cos(x)).
Це і є загальний інтеграл диференціального рівняння.
Його можна залишити як є, а можна сталу перенести в праву сторону
![]()
Обчислення не складні, інтеграли теж в бльшості випадків можна знайти за табличними формулами інтегрування.
Приклад 4. Розв'язати задачу Коші
y'=y+x, y(1)=e3-2.
Розв'язання:Тут вже попередні перетворення не пройдуть. Проте рівняння лінійне і досить просте. В таких випадках потрібно ввести нову змінну
z=y+x.
Пам'ятаючи, що y=y(x) знайдемо похідну від z.
z'= y'+1,
звідки виражаємо стару похідну
y'= z'-1.
Підставимо це все у вихідне рівняння
z'-1=z або z'=z+1.
Розпишемо диф. рівняння через диференціали
dz=(z+1)dx.
Відокремлюємо змінні в рівнянні
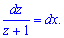
Залишилося обчислити прості табличні інтеграли, які під силу кожному
![]()
Експонуємо залежність, щоб позбутися логарифма при функції
z+1=ex+Сабо z=ex+1-1
Не забуваємо повернутися до виконаної заміни
z=x+y= ex+С-1,
звідси виписуємо загальний розв'язок диференціального рівняння
y= ex+С-x-1.
Знайти розв'язок задачі Коші до ДР в даному випадку не складно. Виписуємо умову Коші
y(1)=e3-2
та підставляємо у тільки що знайдений розв'язок
e1+С-1-1= e3-2.
Звідси отримаємо умову для обчислення сталої
1+С=3; С=3-1=2.
Тепер можемо записати розв'язок задачі Коші (частковий розв'язок ДР)
y= ex+2-x-1.
Якщо Ви добре вмієте інтегрувати, з похідної у Вас справи теж на висоті, тоді тема диференціальних рівнянь для Вас не буде перешкодою в навчанні..
В подальшому навчанні Вам необхідно вивчити декілька важливих схем, щоб навчитися розрізняти рівняння та знати, яка заміна чи методика працює в кожному випадку.
Після цього на Вас чекають однорідні та неоднорідні диференціальні рівняння першого та вищих порядків. Щоб не навантажувати Вас теорією в наступних уроках ми будемо наводити лише тип рівнянь та коротку схему їх обчислень. Всю теорію Ви можете почитати з методичок для вивчення курсу "Диференціальні рівняння" або онлайн ресурси, що містять зрозумілі Вам пояснення теорії диференціальних рівнянь.
Готові відповіді з диф. рівнянь взяті з програми дя математиків ЛНУ ім. І. Франка.
Ми знаємо, як розв'язати диференціальні рівняння і постараємося в легкий спосіб прищепити ці знання Вам!
Що таке загальний і частинний розв'язок ДР, загальний інтеграл ДР та частинний інтеграл Ви можете пригадати з наступної теорії:

Щоб швидко класифікувати диференціальне рівняння та знати як його обчислювати ми вибрали гарні таблиці з літератури, з яких Ви швидко можете знайти відповіді на питання:
Що таке найпростіше диференціальне рівняння?
Які ДР називають рівняннями з віокремлюваними змінними, а які з відокремленими?
Який вигляд мають однорідні ДР?
В чому різниця між однорідними та неоднорідними ДР?
Яке ДР називають рівнянням Бернуллі?
Як перевірити чи маємо рівняння в повних диференціалах?
На ці питання Ви повинні вміти відповідати, бо їх часто задають на практичних та тестах, і за відповіддю викладач швидко може перевірити наскільки добре Ви знаєте основи ДР. Тому перегляньте та запам'ятайте вміст наступних таблиць, а далі уважно розберіть приклади, що ми для Вас підготували.
Класифікація ДР першого порядку
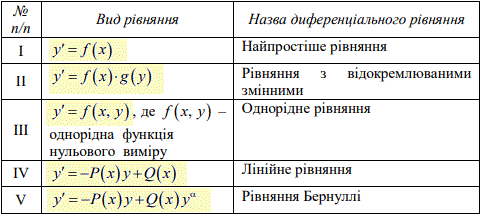
Таблиці 2, 3. Види диференціальних рівнянь
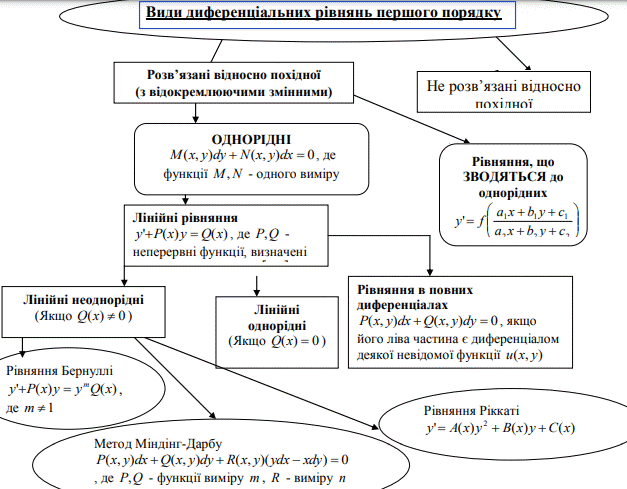
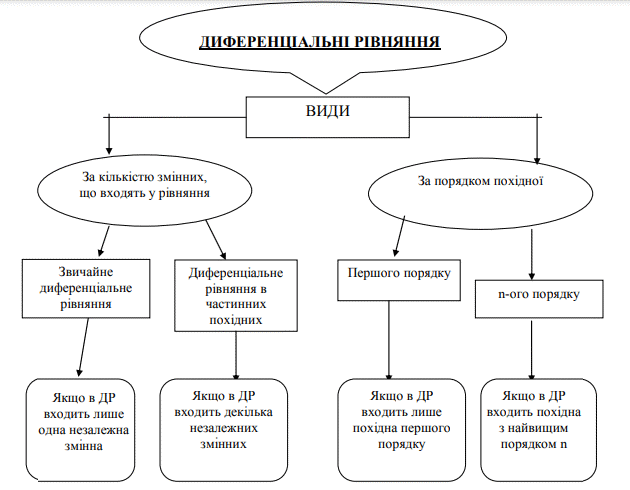
Найпростіші диференціальні рівняння
Приклад 1. Знайти розв'язок ДР
y'=4x
Розв'язування: Маємо найпростіше ДР першого порядку.
При інтегруванні обох її частин отримаємо
y=4x2/2+C=2x2+C - загальний розв'язок ДР.
де C - довільна стала.
Приклад 2. Знайти розв'язок ДР
y'=8x
Розв'язування: З вигляду р-ня робимо висновок що це найпростіше ДР першого порядку.
Похідну y' замінюємо приростом функції до приросту аргументу y'=dy/dx, розділяємо змінні та інтегруємо
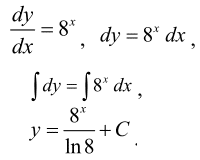
Не забувайте, що невизначений інтеграл рівний значенню інтегралу + стала С.
Приклад 3. Розв'язати задачу Коші
y'=cos(x), y(0)=π.
Розв'язування: Інтегруємо найпростіше ДР першого порядку.
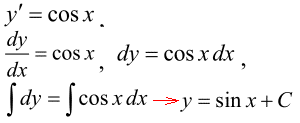
Записуємо y=sin(x)+C - загальний розв'язок ДР.
Обчислимо розв'язок задачі Коші
y(0)=Pi.->π=sin(0)+C,
π=0+C,
C=π.
Підставивиши C=π в загальний розв'язок ДР, отримаємо
y=sin(x)+π - частинний розв'язок заданого ДР.
І подібних умов можна навести тисячі.
При інтегруванні лівої частини отримаєте функцію, а праву слід звести до одного з відомих табличних інтегралів +С.
Ось і вся методика обчислення найпростіших ДР.
Рівняння з відокремлюваними змінними
Приклад 4. Знайти загальний розв'язок ДР
y'=x*(y-1)
Розв'язування: Маємо ДР з відокремлюваними змінними, оскільки права сторона має вигляд f(x)*g(y)
Замінюємо y'=dy/dx, розділяємо змінні та інтегруємо
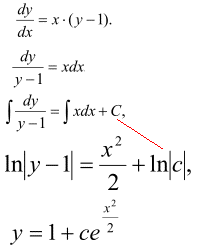
де C=ln(c) - довільна стала.
При розв'язуванні ДР часто сталу С вносять під логарифм чи експоненту, перепепозначають і вже оперують новою сталою.
В такий спосіб добиваються компактного вигляду загального розв'язку ДР та простоти обчислень.
Приклад 5. Знайти розв'язок задачі Коші
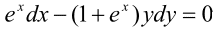
y(0)=2.
Розв'язування: Маємо ДР з відокремлюваними змінними.
В другому рядку формул розділили змінні, тому таке р-ня вже називається - ДР з відокремленими змінними.
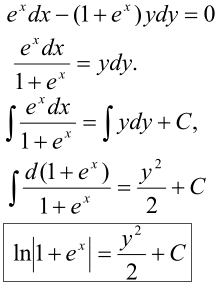
Останніій запис не містить явно вираженої функції y(x) - тому такий запис розв'язку називають загальний інтеграл ДР.
Розв'яжемо задачу Коші:
y(0)=2
Підставляємо в загальний інтеграл ДР
ln(1+1)=22/2+C,
C=ln(2)-4/2=ln(2)-2.
Заміняєємо сталу в загальниому інтегралі ДР та отримаємо
ln(|1+ex|)=y2/2+ln(2)-2 - частинний інтеграл диференціального рівняння.
Розглянемо, ще один приклад де в результаті інтегрування отримаємо загальний інтеграл ДР.
Приклад 6. Розв'язати диференціальне рівняння
x+y*y'=0.
Розв'язування: Бачимо, що можемо розділити змінні, тому таке рівняння є ДР з відокремлюваними змінними.
При інтегруванні обох її частин отримаємо
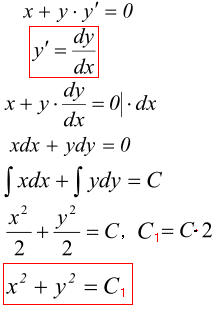
y=4x2/2+C=2x2+C -загальний розв'язок ДР.
C - довільна стала.
Приклад 7. Зінтегрувати рівняння
(1+x^2)y*dx+(1+y^2)x*dy=0
Розв'язування: Розділяємо змінні в ДР та інтегруємо.
При інтегруванні обох її частин отримаємо логарифми, які групуємо за правилом суми логарифмів
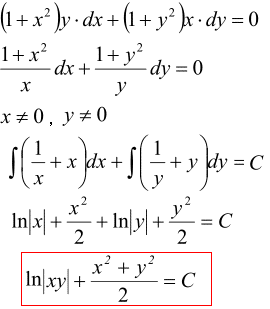
Остання формула містить загальний інтеграл ДР.
(не плутати з загальним розв'язком y(x)=...).
Слід відзначити, що всюди потрібно перевіряти вирази на які ділимо.
Так тут виконували ділення на "x, y", тому слід перевірити чи пара x=0, y=0 не перетворює задане ДР в тотожність.
(1+0)*0*dx+(1+0)*0*dy=0.
Таким чином, точка x=0,y=0 - є особливим розв'язком диференціального рівняння.
Приклад 8. Знайти розв'язок ДР
y'=(4x+y+5)2
Розв'язування: Дане рівняння є звідним до рівнянь з відокремлюваними змінними.
Для цього слід ввести заміну змінних
z=4x+y або z=4x+y+5.
Вибираємо першу з них, диференціюємо, покладаючи z, y за функції, а x -за змінну.
Далі виражаємо y', підставляємо в рівняння, після чого розділяємо змінні та інтегруємо
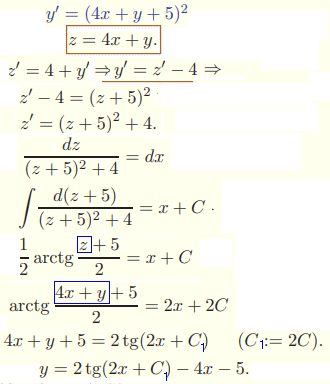
Остання формула має явний вигляд функції y тому це загальний розв'язок ДР.
Тут ми ділили на (z+5)2+4, але оскільки цей вираз завжди додатний, то перевіряти чи він буде особливим розв'язком ДР немає змісту.
В наступних уроках продовжимо знайомитися з методами розв'язування ДР та різними алгоритмами, що дозволяють це робити швидко та правильно.
Студенти Львівського національного університету ім. І. Франка серед відповідей до ДР можуть знайти варіанти, які їх чекатимуть на контрольній. ВУЗи Києва, Одеси, Харкова та інших міст України мають подібну програму з ДР, тому теж знайдуть масу готових прикладів. В загальному теорія з диференціальних рівнянь повністю сформована, тому алгоритмами обчислень незмінні і ними може користуватися кожен, хто вирішив вивчати диференціальні рівняння.
Приклад 1. (1.25) Знайти загальний інтеграл диференціального рівняння
Розв'язання: Маємо диференціальне рівняння першого порядку розписане через диференціали. Схема обчислення рівнянь такого типу полягає у розділенні змінних, в результаті цієї операції отримаємо диференціальне рівняння з відокремленими змінними, розв'язок якого знаходимо інтегруванням. Отже спершу групуємо доданки, що містять dx, dy та переносимо по різні сторони знаку "="
Після цього всі множники, що містить y при dx переносимо до dy, те ж саме проробляємо з множниками , що містять змінну x при dy. У такий спосіб зведемо початкове рівняння до диференціального рівняння з відокремленими змінними
Далі зінтегруємо отриману залежність.
Щоб швидко це зробити чисельники вносимо під диференціал
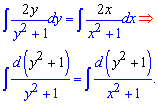
Така маніпуляція дозволяє за допомогою табличного інтегралу отримати логарифми
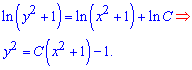
Сталу теж вносимо під логарифм, щоб вкінці прийти до компактного запису загального інтегралу диференціального рівняння. Цю формулу не вартує більше розписувати, оскільки можна не врахувати корені. Більшість би з Вас записала, що функція рівна додатному кореню з правої частини, проте це не правильно. Від'ємний корінь також є розв'язком заданого рівняння, тому якщо записувати, то наступним чином
Проте такий запис важче читати і при формуванні відповіді радимо зупинятися на попередньому кроці.
Більше праці – не завжди означає кращий результат.
Приклад 2. (2.26) Знайти загальний інтеграл диференціального рівняння
![]()
Розв'яязання: Маємо однорідне диференційне рівняння 0 порядку. В цьому легко переконатися, якщо в праву сторону замість x,y підставити t*x,t*y
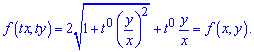
З аналізу правої сторони бачимо, що можемо застосувати підстановку z=y/x, звідси y=z*x.
Не забуваючи, що нова змінна залежить від аргументу виражаємо похідну "y" за правилом добутку
![]()
та з врахуванням заміни переписуємо початкове ДР у вигляді
![]()
Змінну z переносимо в праву сторону
![]()
та розділяючи змінні, переходимо до диференціального рівняння з відокремленими змінними
![]()
Інтегруємо залежність
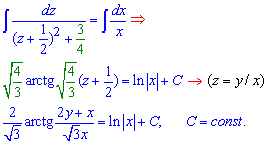
Остання формула і є загальним інтегралом диференціального рівняння. Такий запис ще називають рівнянням не розв'язаним відносно у(х). Виділити у даному випадку у(х) можливо, проте отримаємо менш змістовну формулу ніж кінцева.
Приклад 3. (3.5) Знайти загальний інтеграл рівняння:
![]()
Розв'язання: Задано ДР першого порядку , яке звідне до однорідного диференціального рівняння. Щоб отримати останнє знайдемо стаціонарну точку, для цього розв'яжемо систему рівнянь, яку формуємо прирівнюючи чисельник та знаменник до нуля
![]()
Далі виконуємо зміщення початку координат в знайдену точку O(1;1)
![]() ,
,
Початкове ДР при такій заміні зводимо до вигляду
![]()
Після цього у правій частині змінну X виносимо з чисельника та знаменника за дужки та скорочуємо на неї. В такий спосіб отримаємо однорідне диференціальне рівняння нульового порядку
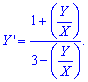
Далі використовуємо схему обчислень з попереднього завдання. Робимо заміну: z=Y/X; Y=z*X, похідна старої функції при цьому виражається формулою
![]()
Підставимо у рівняння та спростимо його
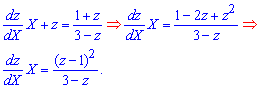
Далі перетворюємо до диференціального рівняння з відокремленими змінними
![]()
та інтегруванням обчислюємо його
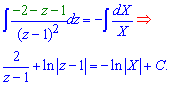
Вертаючись двічі до попередніх замін, отримаємо
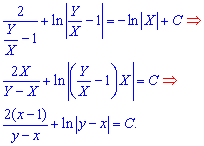
Остання формула і є шуканий загальний інтеграл диференціального рівняння. Вона неявно зв'язує функцію y(x) та аргумент.
Приклад 4. (4.6) Знайти розв'язок задачі Коші:
![]()
Розв'язання: Задано неоднорідне диференціальне рівняння першого порядку. Запишемо та проінтегруємо відповідне однорідне рівняння (ліва частина):
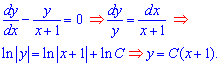
Схема обчислень тут використана стандартна – розділили змінні та про інтегрували. Далі, щоб задовільнити неоднорідну частину рівняння покладаємо, що стала є функцією аргумента C=C(x). Запишемо функцію та її похідну
![]()
Далі підставимо у ДР та після інтегрування знайдемо вигляд сталої C=C(x)
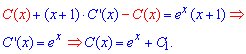
Записуємо загальний розв'язок неоднорідного диференціального рівняння в кінцевому вигляді
![]()
Ров'яжемо задачу Коші. Сталу C1 довизначимо з умови
![]() .
.
Звідси отримаємо
![]() - частковий розв'язок рівняння.
- частковий розв'язок рівняння.
Приклад 5. (5.7) Знайти розв'язок задачі Коші для рівняння Бернуллі
![]()
Розв'язання: Перед Вами новий тип неоднорідних диференціальних рівняння першого порядку. Розділити змінні в цьому випадку є неможливо. Для обчислень такого роду ДР використовуємо схему Бернуллі, робимо заміну змінних y=u*v, y'=u'v+uv', де в добутку фігурують функції u=u(x) і v=v(x) від аргумента. В нових позначеннях ДР приймає вигляд
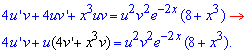
Далі рівняння слід розділити на 2, з яких по черзі визначити функції. Спершу дужку в лівій частині (виділена чорним) прирівняємо до нуля
![]()
Таке ДР для Вас не складне і подібних Ви розв'язували чимало. Записуємо рівняння в диференціалах, далі зводимо до ДР з відокремленими змінними та інтегруючи його знаходимо одну із функцій
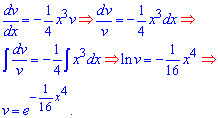
Отримали експоненту з від'ємним показником квадрату аргументу. При підстановці v у початкове ДР отримаємо
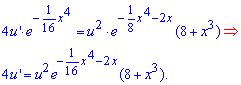
Знову розділяємо змінні та інтегруємо, тільки вкінці тут потрібно додати константу.
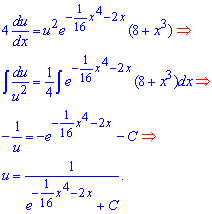
Дві функції ми визначили, можемо записати загальний розв'язок диференціального рівняння.
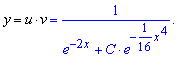
Але це ще не кінець розрахунків. Знайдемо частковий розв'язок диференціального рівняння (задача Коші), для цього пригадаємо початкову умову з якої до визначаємо сталу
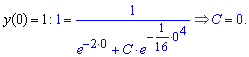
При підстановці С=0 в формулу отримаємо компактний частковий розв'язок диференціального рівняння y=e2x.
Приклад 6. (6.21) Знайти загальний інтеграл диференціального рівняння:
![]()
Розв'язання: Ліва частина ДР може бути повним диференціалом функції двох змінних u(x,y).
Щоб перевірити це знайдемо часткові похідні, зокрема для множника при dx похідну беремо по dy, для іншого по dx. Умова повного диференціалу має вигляд
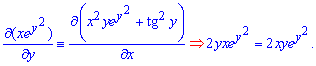
Вона справджується, отже можемо відновити функцію інтегруванням
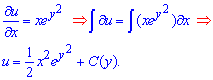
Якщо інтегруємо по аргументу то стала залежна від функції і навпаки. Це важливо, оскільки потрібно, щоб функція задовольняла дві часткові похідні. А для цього диференціюємо знайдену функцію по "ігрик" та прирівнюємо з множником ДР при dy
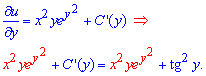
Отримаємо рівняння на похідну від сталої з якого інтегруванням знаходимо C(y)
![]()
Загальний інтеграл диференціального рівняння при цьому рівний
![]()
Приклад 7. Знайти частинний розв'язок диференціального рівняння другого порядку.
x^2y''=(y')^2, y(1)=1/2, y'(1)=1.
Обчислення: Зробимо заміну: y'=p, де p=p(x), тоді y''=p'.
В такий спосіб понизимо степінь ДР, яке обчислюємо методом розділення змінних
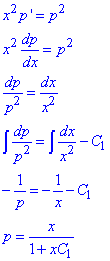
Повернемося до заміни y'=p:
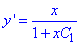
Підставимо початкову умову y'(1)=1 і знайдемо сталу C1:
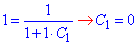
Отримали просте ДР y'=x, розписуємо та інтегруємо:
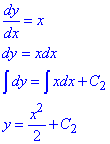
Підставимо початкову умову y(1)=1/2 і знайдемо C2:
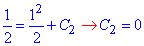
Підставляємо,
y=x^2/2 - частинний розв'язок заданого диференціального рівняння.
Приклад 8. Знайти загальний розв'язок диференціального рівняння другого порядку.
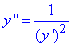
Обчислення: Виконуємо заміну:
y'=p, де p=p(y), тоді y"=p"p. Отож,
Перетворимо ДР
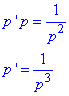
Отримали диференціальне рівняння першого порядку, яке зводиться до рівнянь з відокремлюваними змінними.
Розв'яжемо отримане рівняння:
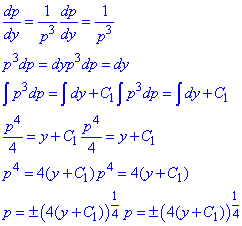
Повернемося до заміни:
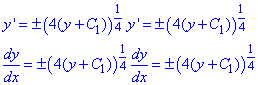
Отримали диференціальне рівняння першого порядку з відокремлюваними змінними.
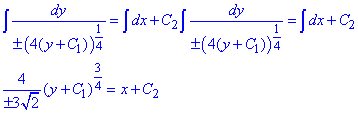
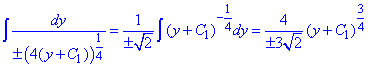 – загальний розв'язок заданого диференціального рівняння.(*)
– загальний розв'язок заданого диференціального рівняння.(*)
На цьому перша частина контрольної роботи розглянута, далі будуть рівняння в повних диференціалах, що потребують визначення інтегруючого множника та неоднорідні диференціальні рівняння 2, 3 порядку.
]]>Приклад 7. (7.22) Знайти інтегруючий множник та розв'язати задачу Коші
![]()
Розв'язання: Запишемо ДР у диференціалах
![]()
Перевіримо чи виконується умова на повний диференціал. Позначимо
![]()
та обчислимо часткові похідні
![]()
З їх значень робимо висновок, що ліва частина рівняння не є повним диференціалом
![]()
Таких завдань не багато і рівняння такого типу називають звідними до рівнянь в повних диференціалах. Для подальших обчислень перевіримо чи допускає ДР інтегруючий множник ?
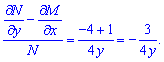
Тут він залежний від функції y. Вам можуть зустрітися завдання, де інтегруючий множник залежить від аргументу, або від добутку y*x. Таким чином встановили, що задане ДР допускає інтегруючий множник, його значення знаходимо за формулою
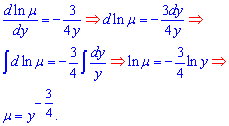
Після множення всіх доданків ДР на "м'ю" отримаємо рівняння
![]()
в повних диференціалах
(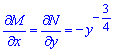 ).
).
Схему обчислення ДР в повних диференціалах Ви вже знаєте, тому для простоти обчислень вибираємо другий множник та після розділення змінних виконуємо інтегрування.
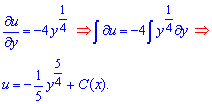
Знаходимо похідну функції за аргументом та довизначаємо сталу
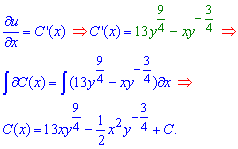
Маємо все для того, щоб записати загальний інтеграл диференціального рівняння
![]()
Розв'яжемо задачу Коші.
Записуємо початкову умову для функції
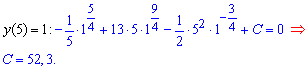
З рівняння знаходимо сталу та підставляємо в частинний інтеграл ДР
![]()
На цьому завдання розв'язано.
Добре перегляньте та випишіть в чорновик схему відшукання інтегруючого множника.
Хто вчиться на математичному факультеті гарантовано буде розбирати подібне диференціальне рівняння.
Приклад 8. (8.10) Знайти загальний розв'язок диференціального рівняння:
![]()
Розв'язання: Маємо неоднорідне диференціальне рівняння другого порядку.
Загальний інтеграл шукаємо у вигляді суми двох функцій
![]()
Спершу розв'язуємо однорідне диференціальне рівняння:
![]()
Для пониження степеня рівняння використовуємо метод параметра
![]()
Рівняння перетвориться до однорідного ДР першого порядку
![]()
Зводимо його до ДР з відокремленими змінними та інтегруємо
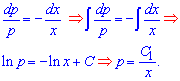
Далі повертаємося до заміни та знаходимо розв'язок однорідного рівняння
![]()
Обидві сталі набувають довільних значень.
Тепер спробуємо проаналізувати просту на вигляд неоднорідну частину рівняння. Щоб друга похідна помножена на "ікс" в 4 степені дорівнювала сталій, функцію підбираємо інтегруванням. Знаки і числа нас не цікавлять, тільки функціональна складова
![]()
Звідси частковий розв'язок рівняння подамо у вигляді
![]()
Щоб знайти коефіцієнт A обчислюємо дві похідні
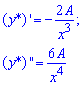
та підставимо в початкове ДР
6A-2A=1; A=1/4.
Можемо записати явний вигляд другої функції
![]()
Додаючи до неї однорідний розв'язок отримаємо загальний розв'язок диференціального рівняння:
![]() ,
,
де C1, C2 - довільні константи.
Приклад 9. (9.11) Знайти загальний розв'язок диференціального рівняння:
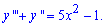
Розв'язання: Маємо неоднорідне диференціальне рівняння третього порядку, тільки в ньому на відміну від попереднього завдання, однорідна частина не містить множників залежних від "ікс".
В такого сорту ДР розв'язок однорідного рівняння шукаємо у вигляді комбінації функцій y=e^k*x.
Підставивши у відповідне однорідне рівняння і спростивши на експоненту отримаємо характеристичне рівняння
k3+k2=0
з якого знайдемо корені
k1=k2=0, k3=-1.
Оскільки обидва корені характеристичного рівняння є дійсні числа, причому - однакові, то розв'язок однорідного рівняння рівний
![]()
Далі проаналізуємо неоднорідну складову рівняння – вона виражається квадратичною функцією, тому частковий розв'язок шукаємо у вигляді
![]()
Знайдемо 3 коефіцієнти, для цього обчислимо похідні
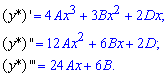
та підставимо у вихідне ДР
![]()
Прирівнюючи коефіцієнти при однакових степенях, складаємо систему рівнянь з якої визначаємо сталі
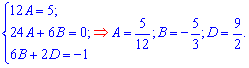
При підставці в формулу часткового розв'язку отримаємо
![]()
Додавши до нього інтеграл однорідного рівняння будемо мати загальний розв'язок ДР
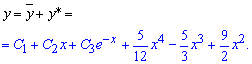
Сталі C1, C2, C3 приймають довільне значення.
Якщо б завдання містило умову Коші то з попередніх завдань Ви могли бачити, як легко можна знайти сталі та забезпечити виконання умови Коші.
Приклад 10. (10.4) Знайти загальний розв'язок диференціального рівняння:
![]()
Розв'язання: Задане неоднорідне диференціальне рівняння третього порядку, однорідна частина якого містить 1-3 похідні функції і не містить аргументів. В такому випадку інтеграл однорідного рівняння шукаємо через експоненту.
Складемо характеристичне рівняння для однорідного ДР та визначимо розв'язки
k3-2k2+k=0 -> k1=0, k2=k3=1.
Отримали дійсні корені характеристичного рівняння, два з яких рівні між собою.
В таких випадках розв'язок однорідного рівняння записуємо формулою
![]()
Неоднорідна частина заданого рівняння (2x+5)e2x має вигляд полінома P(x)e2x, причому степінь експоненти не співпадає з коренями характеристичного рівняння. Це дозволяє шукати частковий розв'язок у вигляді подібному до правої сторони рівняння
![]()
Для визначення сталих A, B необхідно взяти похідні функції
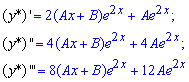
підставити в задане диференціальне рівняння, далі прирівняємо коефіцієнти при однакових степенях "ікс":
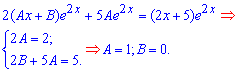
Отримаємо частковий розв'язок ДР
![]()
Загальний розв'язок диференціального рівняння знаходимо сумуванням
![]()
Тільки що Ви навчилися розв'язувати ще один тип диференціальних рівнянь.
Доречі зауважте, що для обчислень в цьому та попередньому завданні ми не застосовували інтегрування.
Приклад 11. (26) Знайти загальний розв'язок диференціального рівняння:
![]()
Розв'язання: Цього разу неоднорідна частина диференціального рівняння другого порядку містить тригонометричні функції.
Розв'язок однорідного ДР шукаємо через експоненти y=exp(k*x),
При підстановці функції в ДР та діленні на експоненту отримаємо залежність з якої знаходимо комплексно спряжені корені характеристичного рівняння, причому лише уявні частини
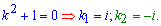
Повертаючись до експонент отримаємо наступне значення кореня однорідного рівняння
![]()
Обов'язково запам'ятайте цей перехід. Інші варіанти таких неоднорідних рівнянь Ви можете розібрати з уроку про комплексні корені характеристичного рівняння.
Частковий розв'язок запишемо у вигляді неоднорідної частини рівняння
![]()
Далі обчислюємо сталі A,B за відомою всім схемою – знаходимо похідні функції та вносимо їх у рівняння
![]()
В результаті прийдемо до тригонометричної залежності, з якої з коефіцієнтів при синусу та косинусу складаємо систему рівнянь, далі визначаємо сталі
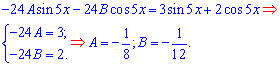
Таким чином ми можемо записати формулу часткового розв'язку ДР
![]()
Підтавляємо знайдені "ігрики" в загальний розв'язок диференціального рівняння:
![]()
Умови Коші в завданні не задано, тому сталі залишаємо як є.
Приклад 12. (22) Знайти загальний розв'язок диференціального рівняння:
![]()
Розв'язання: Перед Вами одне з складних неоднорідних диференціальних рівнянь.
Ліва - однорідна частина, що містить похідні не важка. Проблеми в студентів виникають при відшуканні часткового розв'язку неоднорідного рівняння.
Отож підставимо експоненту в однорідне рівняння та з характеристичного рівняння обчислимо корені
![]()
Отримали комплексно спряжені уявні числа. Такі варіанти в попередніх завданнях розглядалися і у відповідь можемо записати функцію
![]()
Дальше бачимо, що аргументи синуса і косинуса в правій частині ДР співпадають з аргументами розв'язку однорідного ДР (характеристичними числами). В таких випадках частковий розв'язок шукаємо у вигляді правої частини, тільки перед синусом та косинусом додатково має бути множник "ікс".
![]()
Якщо неоднорідна частина не співпадає з однорідним розв'язком, то функцію записуємо без множника.
Далі повторюємо схему попередніх завдань, а саме - знаходимо похідні

Отримані залежності підставимо в початкове ДР, в результаті цього отримаємо рівняння, з якого виписуємо множники при sin(9x), cos(9x), e9x
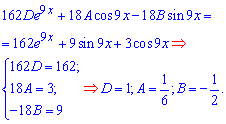
Система рівнянь настільки проста, що для визначення сталих ні методу Гауса, ні Крамера застосовувати не потрібно.
Кожне з рівнянь системи містить тільки одну сталу.
Три знайдені сталі (константи) підставимо в частковий розв'язок ДР
![]()
Додаємо дві функції разом та записуємо загальний розв'язок диференціального рівняння
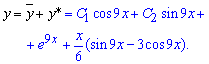
Усі завдання вирішені, методика обчислень диференціальних рівнянь детально розжована, подібні завдання можете переглянути в тій же категорії статей.
На контрольній, модулях чи екзаменах Вам обов'язково доведеться вирішувати завдання на ДР подібного типу. Тому наведені відповіді до контрольної роботи з диференціальних рівнянь детально перегляньте, основні схеми та прийоми занотуйте та використовуйте на практиці.
Якщо бачите, що навчитися до такого рівня Вам не під силу, то завжди можете звернутися за допомогою.
Ми допомогли багатьом студентам успішно скласти іспити, зможемо виручити і Вас!
Диференціальне рівняння першого порядку, які можна записати формулою
N(х)dx+М(у)dy=0 (1)
називають рівнянням з відокремленими змінними.
Їх не важко виявити серед інших рівнянь, основна ознака - коефіцієнти при dx та dy є функції (чи константи), які залежать лише від х при можнику dx та у при dy.
Щоб знайти загальний розв'язок (загальний інтеграл) рівняння з відокремленими змінними необхідно проінтегрувати рівняння (1)
Int(N(x), x) + Int(M(y),y) = С,
Для розуміння диференціальне рівняння (1) можна приймати, як умову рівності нулю повного диференціалу деякої функції двох змінних U(x,y)
Звідси слідує, що функція U(x,y)=С=const рівна сталій.
Диференціальне рівняння вигляду
f1(x)g1(y)dx+f2(x)g2(y)dy=0 (2)
називають диференціальним рівнянням з відокремлюваними змінними в симетричній формі.
В рівнянні (2) коефіцієнти при диференціалах dx та dy є добутками двох функцій: одна залежить тільки від x , а друга — від y . В області, де g1(y), f2(x) приймають відмінні від нуля значення рівняння з відокремлюваними змінними (2) зводиться до рівняння з відокремленими змінними
Звучить як гра слів: відокремленими, відокремлюваними, проте між ними як бачите є маленька різниця, і тепер Ви її знаєте.
Розглянемо типові для практики завдання на диф. рівняння, які в досить простий спосіб можна звести до рівнянь з відокремленими змінними.
Приклад 1 (1.9) Знайти загальний інтеграл диференціального рівняння
![]() Розв'язання: Маємо диференціальне рівняння першого порядку, за теорією його можна назвати рівняння з відокремлюваними змінними записане в диференціалах. Для його спрощення згрупуємо доданки, що містять dx, dy по різні сторони знаку рівності
Розв'язання: Маємо диференціальне рівняння першого порядку, за теорією його можна назвати рівняння з відокремлюваними змінними записане в диференціалах. Для його спрощення згрупуємо доданки, що містять dx, dy по різні сторони знаку рівності
![]()
Далі виділимо спільні множники для кожної суми та перепишемо рівняння у диференціалах до вигляду
![]()
Після цього все, що містить y переносимо до dy, те ж саме проробляємо з множниками , що містять змінну x. В результаті прийдемо до диференціального рівняння з відокремленими змінними
![]()
Тепер погляньте, чому дане рівняння називається з відокремленими змінними?- біля dx маємо функцію лише від "ікс", біля dy - лише від y.
Зінтегруємо диференціальне рівняння
![]()
Виносимо множнии, щоб при змінних в знаменниках стояли одиниці. Також, щоб в чисельнику отримати диференціали знаменника множимо обидві частини на 2
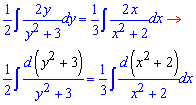
Це дозволяє спростити обчисення та після інтегрування отримати логарифми
![]()
Константу рекомендуємо внести під логарифм, для цього записуйте завжди її у вигляді C1=ln(C)
![]()
Щоб розкрити логарифми експонуємо (знаходимо експоненту) праву і ліву сторону рівняння
![]()
та виділяємо значення функції із отриманої залежності
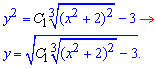
Кінцеве значення, що мітить подвійний корінь і є загальним інтегралом рівняння з відокремлюваними змінними.
Приклад 1*. Знайти частинний розв'язок диференціального рівняння (ДР) зі змінними, що розділяються.
y'=(2y-3)tg(x), y(2π)=6.
Обчислення: Запишемо рівняння в диференціалах, розділимо змінні та проінтегруємо диференціальне рівняння
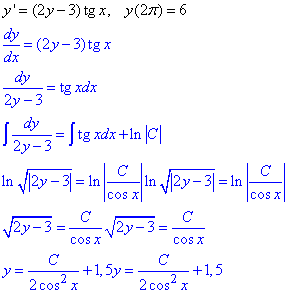
Остання формула є загальним розв'язком ДР.
Розв'яжемо задачу Коші, тобто підставимо початкову умову y(2π)=6 в загальний розв'язок ДР:
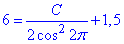 , звідси C=9.
, звідси C=9.
Остаточно, розв'язок задачі Коші:
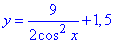 частинний розв'язок рівняння.
частинний розв'язок рівняння.
Приклад 2 (1.3) Знайти загальний інтеграл диференціального рівняння
![]() Розв'язання: Маємо рівняння в диференціалах першого порядку. Розділимо в рівнянні змінні, що містяться при dx, dy та перенесемо їх по різні сторони знаку рівності
Розв'язання: Маємо рівняння в диференціалах першого порядку. Розділимо в рівнянні змінні, що містяться при dx, dy та перенесемо їх по різні сторони знаку рівності
![]()
З перших дужок виносимо спільний для двох доданків множник y за дужки
![]()
Далі перегруповуємо множники так, щоб при dy отримати функцію лише від y, а при dx – функцію аргумента x. В результаті дістанемо диференціальне рівняння з відокремленими змінними
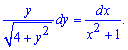
Після інтегрування

отримаємо кореневу залежність для y та арктангенс в результаті обчислення інтегралу від аргументу (права сторона).
![]()
Спробуємо записати розв'язок диференціального рівняння у вигляді залежності y(x). Для цього підносимо обидві частини до квадрату
![]()
та перенісши сталу в праву сторону, обчислюємо корінь квадратний
![]()
Це і є шуканий розв'язок диференціального рівняння.
Приклад 3 (1.15) Знайти загальний інтеграл диференціального рівняння
![]() Розв'язання: Дане рівняння необхідно звести під правило розв'язування рівнянь з відокремленими змінними. Для цього другий доданок, що зі знаком мінус, переносимо в праву сторону від знаку рівності
Розв'язання: Дане рівняння необхідно звести під правило розв'язування рівнянь з відокремленими змінними. Для цього другий доданок, що зі знаком мінус, переносимо в праву сторону від знаку рівності
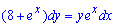
та розділяємо змінні
![]()
Далі інтегруємо праву та ліву сторону залежності
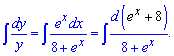
В результаті прийдемо до логарифмічного рівняння.
![]()
І знову нагоошуємо, що в такому вигляді як правило так не записують.
Доцільно, для компактності кінцевого розв'язку, сталу вносити під логарифм, тобто записувати
![]()
Потенціюючи (беручи експоненту) праву і ліву частину формули прийдемо до кінцевого вигяду розв'язку диференціального рівняння
![]()
Як Ви могли переконатися, приклади достатньо прості, методика обчислень диф. рівнянь легка для вивчення.
Приклад 4 (1.16) Знайти загальний інтеграл диференціального рівняння
![]() Розв'язання: Один з доданків (що не містить похідної ) переносимо за знак рівності
Розв'язання: Один з доданків (що не містить похідної ) переносимо за знак рівності
![]()
та записуємо рівняння в диференціалах.
![]()
Наступним кроком зводимо залежність до диференціального рівняння з відокремленими змінними.
Для заданого рівняння всього на всього перехресним діленням записуємо корені в знаменники
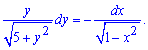
В такому вигляді можемо інтегрувати рівняння
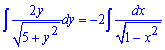
Ліва сторона, що містить функцію дасть в результаті кореневу залежність, при інтегруванні правої сторони за формулами отримаємо арксинус.
![]()
Виконуємо маніпуляції з коренем, щоб отримати залежність вигляду y=y(x)
![]()
Розв'язок диференціального рівняння матиме вигляд
![]()
На цьому ввідний урок завершено і основні висновки Ви повинні зробити самостійно.
Для закріплення теми рекомендуємо самостійно вирішити декілька із наступних завдань
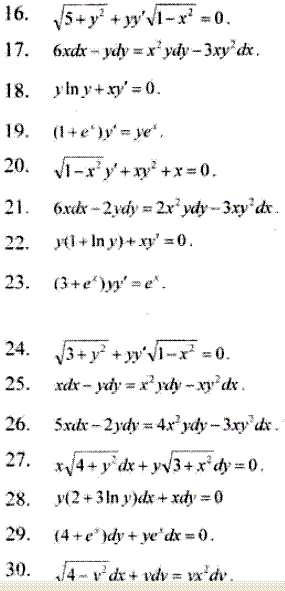
Хочете вірте, а хочете - ні, але це найпростіший тип диференціальних рівнянь, з яким Ви стикнетися на контрольній, екзаменах, практичних заняттях, модулях. Це можна сказати найважливіша частина, оскільки складні диференціальні рівняння доведеться спрощувати та зводити до рівнянь з відокремленими змінними.
Схему обчислень повинні завчити та знати на зубок - це один з основних методів розв'язування складних прикладів на диф. рівняння.
Завдання, що тут розписані взяті із збірника задач з курсу «Диференціальні рівняння». Бокало М. М (ЛНУ ім. І. Франка).
Рівняння з відокремлюваними змінними та звідні до них
Приклад 1.23 Розв'язати диференціальне рівняння 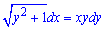
Розв'язання: Перенесемо всі доданки в ліву сторону і отримаємо ДР в симетричній формі:
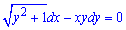
Розділивши обидві частини рівняння на добуток 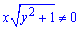 , отримаємо рівняння з відокремленими змінними
, отримаємо рівняння з відокремленими змінними
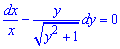
Проінтегруємо останнє рівняння
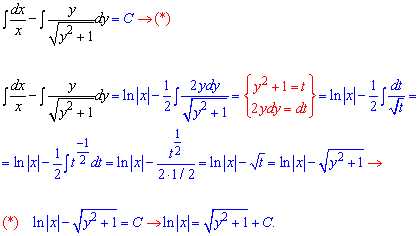
Щоб розкрити другий інтеграл використали заміну змінних
y2+1=t, 2y*dy=dt.
Крім цього, розв'язками заданого диференціального рівняння можуть знаходитись серед виразів, на які ми ділимо, тобто x=0.
Підстановка в початкове рівняння підтверджує, що x=0 є особливим розв'язком ДР.
Отже 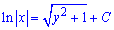 і x=0 - загальний інтеграл диференціального рівняння.
і x=0 - загальний інтеграл диференціального рівняння.
Приклад 1.26 Розв'язати задачу Коші для диференціального рівняння
y'=3y2/3, y(2)=0.
Розв'язання: Розписуємо похідну функції та відокремлюємо змінні.
Далі застосовуємо невизначений інтеграл та проводимо обчислення
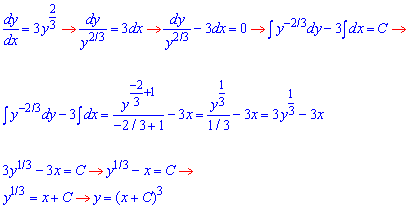 (*)
(*)
При розділенні змінних ділили на y, тому прирівнюємо його до нуля і перевірити чи при цьому початкове ДР перетворюється в тотожність. В даному прикладі y=0 є особливим розв'язком диференціального рівняння.
Підсумовуючи все вище, маємо y=(x+С)3 і y=0 - два загальні розв'язки рівняння.
Далі розв'язуємо задачу Коші, тобто задовільнимо початкову умову y(2)=0:
0=(2+C)3 , звідси C=-2.
Отож, підставляємо сталу С в рівняння (*), та записуємо розв'язок задачі Коші:
y=(x-2) 3.
Приклад 1.28 Розв'язати диференціальне рівняння 2x2yy'+y2=2
Розв'язання: Перетворимо наведену диференційну залежність до ДР з відокремленими змінними. Далі інтегруванням обчислюємо загальний розв'язок диференціального рівняння. Більше інформації про проміжні обчислення дають наступні формули
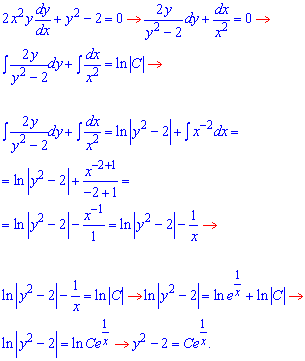
Врахуємо, що вираз на який ділили теж може бути розв'язком ДР.
Тоді y2-2=0, звідси два значення 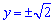 .
.
Можемо зауважити, що ці ж значення коренів отримаємо при C=0, тому вона входить в 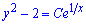 - загальний розв'язок рівняння.
- загальний розв'язок рівняння.
Приклад 1.31 Розв'язати диференціальне рівняння z'=10x+z.
Розв'язання: Враховуючи властивості показників, розписуємо показникову частину та зводимо до ДР з розділеними змінними.
Далі інтегруванням знаходимо розв'язок ДР
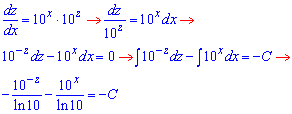
Дану відповідь можна спростити, внісши знаменник ln(10) під сталу.
В результаті отримаємо
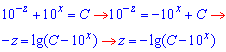
загальний розв'язок рівняння у явному вигляді.
Приклад 1.36 Знайти розв'язок задачі Коші 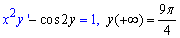
Розв'язання: Маємо ДР першого порядку. Спершу позбудемося неоднорідності, для цього косинус подвійного аргументу розпишемо за тригонометричною формулою.
Далі розділяємо змінні та інтегруванням знаходимо розв'язок ДР у явному вигляді
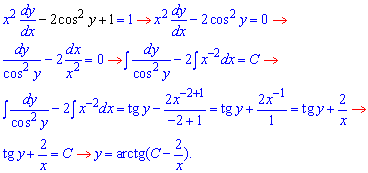
Також врахуємо множник на який ділили рівняння cos2(y), він також буде розв'язком ДР:
cos2(y)=0, звідси
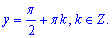
Остаточно отримали
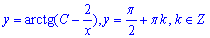 - загальний розв'язок рівняння.
- загальний розв'язок рівняння.
Задовільнимо умову Коші:
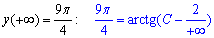
звідси C=1.
Отож, розв'язок задачі Коші прийме значення
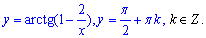
Приклад 1.37 Знайти розв'язок ДР 3y2y'+16x=2xy3, y(x) - обмежена при змінній прямуючій до безмежності  .
.
Розв'язання: Алгоритм обчислень полягає в розділенні змінних, а це не завжди легко бачити. В одних випадках достатньо винести спільний множник за дужки, в інших застосувати властивості показникових чи тригонометричних функцій. Підходи в кожному випадку різняться, головна мета – розділити змінні, щоб біля dx мали змінні в чисельнику чи знаменнику від x, при dy функцію від y.
Лише тоді маємо право до обох частин застосувати невизначений інтеграл
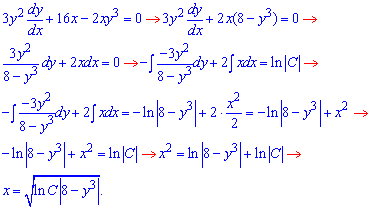
Тут простіше було виразити явний вигляд оберненої функції x(y).
Обов'язково перевіряйте на рівність нулю множник на який ділили при розділенні змінних.
В цьому завданні матимемо умову 8-y3=0, звідси y=2 - особливий розв'язок ДР.
Звідси y=2 - входить до загального розв'язку рівняння, крім цього задовольняє умову Коші.
Приклад 1.39 Розв'язати задачу Коші для ДР
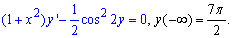
Розв'язання: Розділимо змінні в диференціальному рівнянні, після чого інтегруємо його
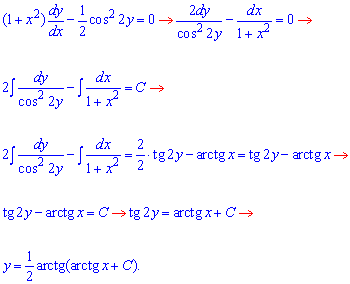
Перевіримо множник на який виконували ділення.
Отримаємо cos2(y)=0,
звідси 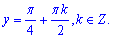
Тому
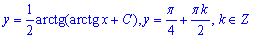
загальний розв'язок рівняння.
Задовільнимо умову Коші
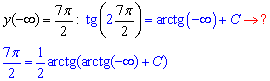
звідси C=Pi/2.
Отож, розв'язок задачі Коші:
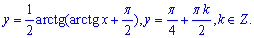
Приклад 1.43 Знайти загальний розв'язок ДР
y'-y=2x-3
Розв'язання: Переносимо змінну в праву частину y'=y+2x-3, далі виконуємо заміну змінних z=y+2x-3, тоді y'+2=z', звідки похідна y'=z'-2, z'-2=z, z'-2-z=0.
Проводимо інтегрування ДР
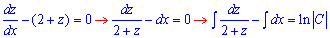
ln|2+z|-x=ln|C|,
ln|2+z|=ln(ex)+ln|C|,
2+z=Cex,
z= Cex-2.
Повернемося до початкових змінних:
y+2x-3= Cex-2,
y= Cex-2x+1.
Врахуємо, що ділили на вираз
2+z=0 маємо z=-2,
звідки y+2x-3=-2, y=1-2x
Однак таке значення отримаємо при С=0 із загальної формули.
Тому y= Cex-2x+1 - єдиний розв'язок диф. рівняння.
Приклад 1.44 Розв'язати задачу Коші
(x+2y)y'=1, y(0)=-1.
Розв'язання: Тут необхідно застосувати заміну x+2y=z (*), тоді 1+2y'=z', звідки
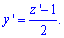
Підставляємо в початкову залежність
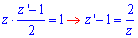
Далі зводимо до рівняння з відокремленими змінними та інтегруємо останнє
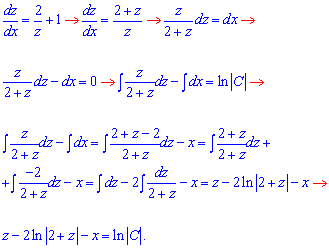
Повернемося до початкових змінних:
x+2y-2ln|2+x+2y|-x=ln|C|,
2y-2ln|2+x+2y|=ln|C|,
ln(ey)=ln|C(2+x+2y)|,
ey=C(x+2y+2).
Врахуємо, що 2+z=0, звідси z=-2, звідки (*) ще одне рішення x+2y+2=0.
ey=C(x+2y+2), x+2y+2=0 - загальний розв'язок рівняння.
Розв'яжемо задачу Коші y(0)=-1:
e-1=C(0-2+2), звідси стала не існує 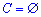 .
.
Отож, розв'язок задачі Коші:
x+2y+2=0.
Приклад 1.46 Знайти загальний інтеграл диф. р-ня
y'=sin(x-y).
Розв'язання: Зробимо заміну x-y=z, тоді 1-y'=z', звідки y'=1-z',
1-z'=sin(z), z'=1-sin(z)
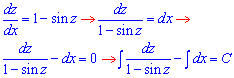
При інтегруванні треба використати заміну
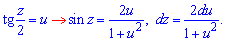
тоді і. (через громіздкі записи, цей інтеграл не розписую детально). (*)
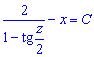
Повернемося до початкових змінних:
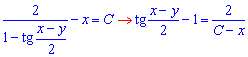
Врахуємо, що 1-sin(z)=0, звідси
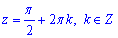 , звідки
, звідки
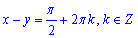
Підсумовуючи всі обрахунки запишемо загальний інтеграл ДР
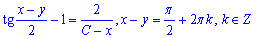
Приклад 1.47 Знайти загальний інтеграл диф. р-ня (x+y)2y'=a2,
Розв'язання: Заміна змінних для диференціального р-ня наступна
x+y=z, тоді 1+y'=z', звідки y'=z'-1.
При цьому початкове рівняння перетвориться до вигляду
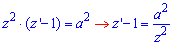
Записуємо рівняння в диференціалах, розділяємо змінні та переходимо до інтегрування
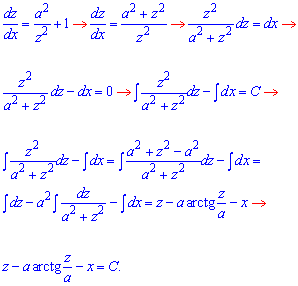
В формулі вище описані всі маніпуляції з підінтегральними функціями, що дозволяє напряму застосувати табличні інтеграли. На цьому не будемо наголошувати, але для себе аналізуйте та вивчайте наведені прийоми. Таким чином не тільки навчитеся розв'язувати диф. р-ня, а й отримаєте досвід інтегрування.
Повернемося до початкових змінних:
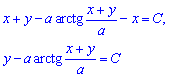 або
або
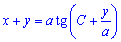 - загальний розв'язок рівняння.
- загальний розв'язок рівняння.
Приклад 1.84 Знайти загальний інтеграл ДР (x-2y-1)dx+(3x-6y+2)dy=0,
Розв'язання: Перетворимо ДР до наступної форми
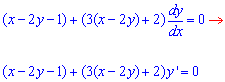
Це дозволяє застосувати наступну заміну змінних
x-2y=z, тоді 1-2y'=z', звідки y'=(1-z')/2.
Розпишемо ДР
z-1+(3z+2)(1-z')/2=0,
2(z-1)+(3z+2)(1-z')=0,
2z-2+3z-2-(3z+2)z'=0.
Далі переходимо до рівняння з відокремленими змінними та виконуємо інтегрування
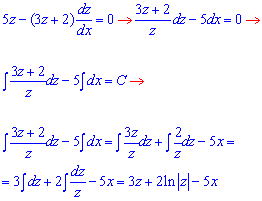
3z+2ln|z|-5x=C.
Отриманий розв'язок записаний в нових змінних, тому необхідно перейти до початкових:
3(x-2y)+2ln|x-2y|-5x=C. або ln|x-2y|=x+3y+C.
Врахуємо множник на який ділили початкове ДР, з умови z=0 маємо x-2y=0 особливий розв'язок ДР.
Тому отримали ln|x-2y|=x+3y+C, x-2y=0 - загальний розв'язок рівняння.
Приклад 1.86 Знайти загальний інтеграл ДР (x-2y+1)dx-(2x+4y+3)dy=0,
Розв'язання: Маємо ще одне задання, подібне до попереднього.
Запишемо ДР через похідну
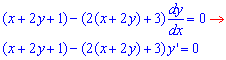
Заміна змінних x+2y=z, 1+2y'=z',y'=(z'-1)/2
зведе початкове ДР до наступного
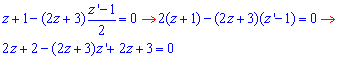
Далі розділяємо змінні та інтегруємо рівняння з відокремленими змінними
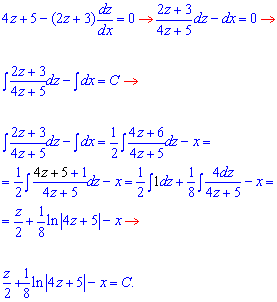
ln|4z+5|=8x-4z+C.
Повернемося у відповіді від z до x, y:
ln|4(x+2y)+5|=8x-4(x+2y)+C,
ln|4(x+2y)+5|=4x-8y+C.
Врахуємо значення на яке ділили. Прирівнюємо до нуля
4z+5=0
і переконуємося що пряма 4x+8y+5=0 є особливим р-ком ДР
Тому 2 р-ня ln|4(x+2y)+5|=4x-8y+C, 4x+8y+5=0 складають загальний інтеграл диференціального рівняння.
Для вивчення даної теми рекомендумаємо самостійно вправлятися з подібними завданнями і вправлятися багато.
На початкових етапах можете не інтегрувати диференціальне рівняння, просто вивчити всі можливі прийоми та заміни змінних, що дозволяють отримати ДР з відокремленими змінними.
Далі можна рухатися в сторону інтегрування диференціальних рівняннь та задовільнення крайових умов (задачі Коші), якщо такі задані.
Рівняння виду P(x,y)dx+Q(x,y)dy=0, де функції P(x,y) і Q(x,y) є однорідними функціями одного порядку називають однорідним диференціальним рівнянням (ОДР).
Схема розв'язання однорідного диференціального рівняння
1. Спершу потрібно застосувати підстановку y=z*x, де z=z(x) – нова невідома функція (в такий спосіб вихідне рівняння зводиться до диференціального рівняння з відокремлюваними змінними (ДРВЗ).
2.Похідна добутку y'=(z*x)'=z'*x+z*x'=z'*x+z або в диференціалах dy=d(zx)=zdx+xdz.
3.Підставляємо нову функцію у та її похідну y'(або dy) в ДР з відокремлюваними змінними відносно x та z.
4.Розвязавши диференціальне рівняння з відокремлюваними змінними, зробимо обернену заміну y=z*x, тому z= y/х, і отримаємо загальний розв'язок (загальний інтеграл) диференціального рівняння.
5.Якщо задано початкову умову y(x0)=y0, то знаходимо частинний розв'язок задачі Коші. В теорії все звучить легко, протее на практиці не у всіх так весело виходить рішати диф. рівняння. Тому для поглиблення знань розглянемо поширені приклади. На легких завданнях немає особливо, що Вас навчити, тому зразу перейдемо до складніших.
Обчислення однорідних диференціальних рівнянь
Приклад 1. (2.8) Знайти загальний інтеграл диференціального рівняння
![]()
Розв'язання: Ділимо праву сторону рівняння на змінну, яка стоїть множником біля похідної. В результаті прийдемо до однорідного диференційного рівняння 0 порядку
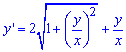
І тут багатьом мабуть стало цікаво, як визначити порядок однорідного рівняння? Питання достатньо доречне, а відповідь на нього наступна: в праву сторону підставляють замість функції та аргумента значення t*x, t*y. При спрощенні отримують параметр "t" в певному степені k, його і називають порядком рівняння. В нашому випадку "t" скоротиться, що рівносильно 0-му степені або 0-му порядку однорідного рівняння.
Далі в правій стороні можемо перейти до нової змінної y=zx; z=y/x .
При цьому не забуваємо виразити похідну "y" через похідну нової змінної. За правилом частки знаходимо
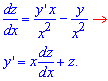
Рівняння в диференціалах набуде вигляду
![]()
Спільні доданки в правій і лівій частині скорочуємо та переходимо до диференціального рівняння з відокремленими змінними.
![]()
Інтегруємо обидві частини рівняння
![]()
Для зручності подальших перетворень постійну зразу вносимо під логарифм
![]()
За властивостями логарифмів отримане рівняння еквівалентне наступному
![]()
На цьому рівняння ще не розв'язане, необхідно повернутися до виконаної заміни змінних
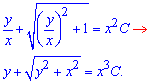
Це і є загальний розв'язок диференційного рівняння. Якщо Ви уважно читали попередні уроки, то ми наголошували, що схему обчислення рівнянь з відокремленими змінними ви повинні вміти застосовувати вільно і такі рівняння доведеться обчислювати для складніших типів ДР.
Приклад 2. (2.14) Знайти загальний інтеграл диференціального рівняння
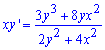
Розв'язання: Схема обчислень однорідних та звідних до них ДР Вам знайома. Переносимо змінну в праву сторону рівняння, а також в чисельнику та знаменнику виносимо x2, як спільний множник
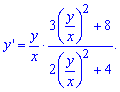
В такий спосіб отримаємо однорідне ДР нульового порядку.
Наступним кроком вводимо заміну змінних z=y/x, y=z*x, про яку постійно будемо нагадувати, щоб Ви її завчили
![]()
Після цього ДР зводимо до вигляду
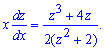
Далі перетворимо залежність до диференціального рівняння з відокремленими змінними
![]()
та інтегруванням розв'язуємо його.
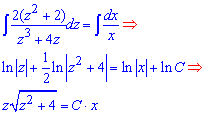
Інтеграли не складні, решта перетворень виконано на основі властивостей логарифма. Остання дія включає експонування логарифма. Вкінці повертаємося до початкової заміни та записуємо розв'язок диференціального рівняння
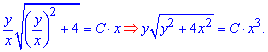
Константа "C" приймає будь-яке значення. Всі хто навчається заочно мають проблеми на екзаменах з даним типом рівнянь, тому просьба уважно переглянути та запам'ятати схему обчислень.
Приклад 2*. Знайти загальний розв'язок однорідного диференціального рівняння першого порядку.
xy'-y'=(x+y)ln((x+y)/x).
Обчислення: Розділимо обидві частини рівняння на "ікс"
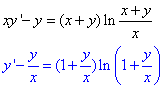
зробимо заміну y=z•x, тобто z=y/x.
Підставимо в ДР, розділимо змінні та розв'яжемо шляхом інтегрування:
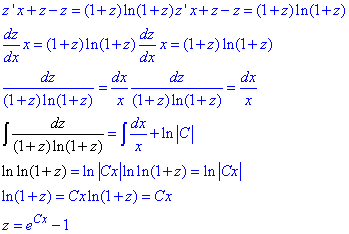
Повернемося до початкових змінних "z=y/x":
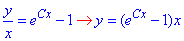 - загальний розв'язок рівняння.
- загальний розв'язок рівняння.
При інтегруванні лівої частини рівняння використали заміну змінних
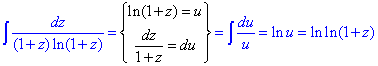
Приклад 3. (2.16) Знайти загальний інтеграл диференціального рівняння
![]()
Розв'язання:Як слідує з наведеної вище методики, диференціальні рівняння такого типу розв'язують методом введення нової змінної. Перепишемо залежність так, щоб похідна була без змінної
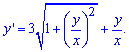
Далі з аналізу правої частини бачимо, що всюди присутня частка, її і позначаємо за нову невідому z=y/x, y=z*x.
Знаходимо похідну від y
![]()
З врахуванням заміни початкове ДР перепишемо у вигляді
![]()
Однакові доданки спрощуємо, а все що отримали зводимо до ДР з відокремленими змінними
![]()
Інтегруванням обох частин рівності
![]()
приходимо до розв'язку у вигляді логарифмів
![]()
Експонуючи залежності загальний розв'язок рівняння зводимо до запису
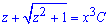
який після підстановки у нього початкової заміни змінних набуде вигляду
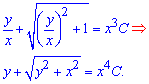
Тут С – стала, яку можна довизначити з умови Коші. Якщо не задана задача Коші то стала приймає довільне дійсне значення.
Ось і вся мудрість в обчисленні однорідних диференціаьних рівнянь.
Далі будуть проаналізовані непрості з точки зору обчислень однорідні ДР, які містяться в збірнику задач з курсу «Диференціальні рівняння», (Бокало М. М.).
Тому уважно розбирайте всі перетворення та заміни, що описані у формулах переходу від одного р-ня до іншого ДР, оскільки описати все та зробити наголоси на дрібних речах не завжди є можливо.
Методика обчислення однорідних диференціальних рівнянь
Приклад 2.60 Знайти загальний інтеграл диференціального рівняння
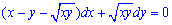
Розв'язання: З вигляду р-ня бачимо, що ніяким чином його не можна звести до диференціального рівнянь з відокремленими змінними, оскільки маємо попарні добутки змінних.
Але бачимо, що функції 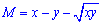 і
і 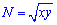 - є однорідними функціями першого степеня.
- є однорідними функціями першого степеня.
Тому поділимо рівняння на x (зауважимо, що змінну можна представити у вигляді добутку 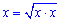 ) :
) :
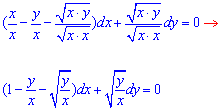
зробимо заміну змінних y=z*x, тоді dy=x*dz+z*dx,
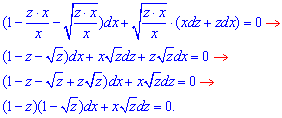
Отримали диференціальне рівняння з відокремлюваними змінними:
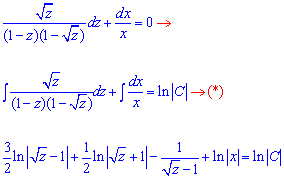
далі зробимо елементарні перетворення, використовуючи властивості логарифмічної, степеневої і показникової функції:
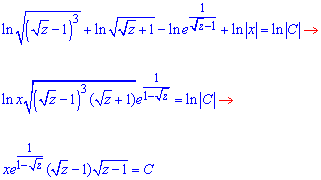
Повернемося до початкових змінних (z=y/x):
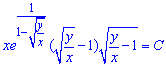
далі знову спростимо вираз
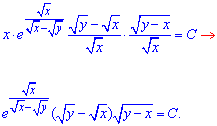
Крім цього, розв'язками заданого диференціального рівняння можуть знаходитись серед виразів, на які ми ділили, тобто x=0, 1-z=0 і 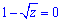 .
.
Але при C=0 розв'язок вже містить 1-z=0 і 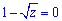 звідки
звідки
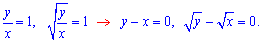
Тому отримали 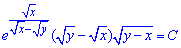 - загальний інтеграл рівняння і x=0 - особливий розв'язок.
- загальний інтеграл рівняння і x=0 - особливий розв'язок.
-------------------------------------------------
Вище мали інтеграл (*), його обчислення наведено далі:
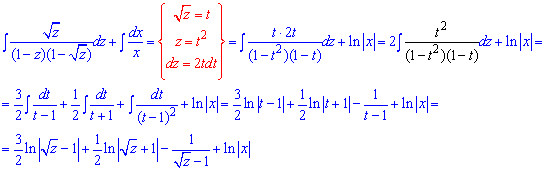
Дріб 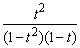 розклали методом невизначених коефіцієнтів:
розклали методом невизначених коефіцієнтів:
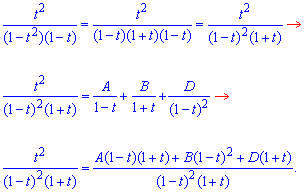
t2=A-At2+B-2Bt+Bt2+D+Dt,
1*t2+0*t+0=(-A+B)t2+(-2B+D)t+(A+B+D),
прирівнюємо коефіцієнти при однакових степенях t, та розв'язуємо систему рівнянь, отримаємо A=-3/4, B=1/4, D=1/2.
Звідки отримаємо наступний розклад дробу на прості множники
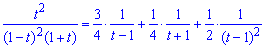
На цьому і всі розрахунки до заданого прикладу.
Приклад 2.65 Знайти розв'язок диференціального рівняння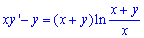
Розв'язання: Поділимо ДР на змінну х
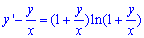
далі робимо заміну y=z*x, тоді y'=z'*x+z,
z'*x+z-z=(1+z)ln(1+z).
Переходимо до ДР з відокремленими змінними та виконуємо інтегрування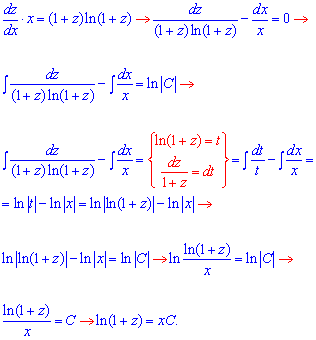
Повернемося до початкових змінних: 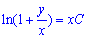 - загальний інтеграл рівняння.
- загальний інтеграл рівняння.
Приклад 2.72 Розв'язати диф. р-ня
(13x+y)dx+(y-5x)dy=0
Розв'язання: Ділимо на аргумент, щоб переконатися що маємо однорідне диф. р-ня
(13+y/x)dx+(y/x-5)dy=0,
а далі виконуємо заміну змінних y=z*x, тоді dy=x*dz+z*dx,
(13+z)dx+(z-5)(x*dz+z*dx),
13dx+z*dx+zx*dz-5x*dz+z2dx-5z*dx=0 ,
x(z-5)dz+(z2-4z+13)dx=0.
Розділяємо змінні та інтегруємо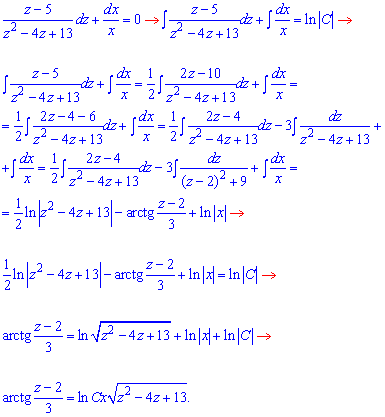
Отримали арктангенс та логарифм (за правилом суми логарифмів).
Повернемося до початкових змінних:
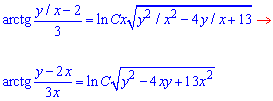 - загальний інтеграл рівняння.
- загальний інтеграл рівняння.
Приклад 2.59 Знайти загальний інтеграл диференціального рівняння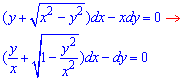
Розв'язання: Зробимо заміну змінних y=z*x, тоді dy=x*dz+z*dx,
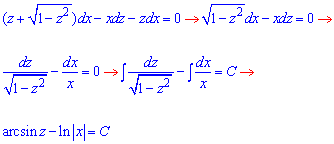
Повернемося до початкової заміни:
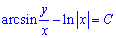
Врахуємо, що 1-z2=0 і x=0, звідси z=1,z=-1 і x=0.
Тому 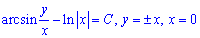 - загальний розв'язок рівняння.
- загальний розв'язок рівняння.
Приклад 2.81
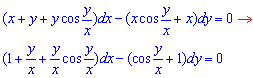
Розв'язання: Виконуємо заміну y=z*x, тоді dy=x*dz+z*dx,
(1+z+z*cos(z))dx-(cos(z)+1)( x*dz+z*dx)=0, відкриємо дужки і спростимо вираз:
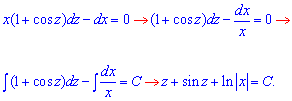
Повернемося до початкових змінних:
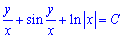 - загальний інтеграл ДР.
- загальний інтеграл ДР.
Уважно перегляньте наступні приклади, а саме - схеми обчислення ДР,
можливо комусь вони допоможуть на практичних чи екзамені.
Приклад 2.94 Знайти загальний інтеграл диференціального рівняння
(2y-1)dx+(2x+y+1)dy=0,
Розв'язання: Складемо систему рівнянь і розв'яжемо її:
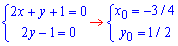
звідси
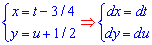
маємо
2u*dt+(2t+u)du=0,
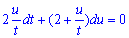
Зробимо заміну u=z*t, тоді z=u/t тоді
du=t*dz+z*dt, 2z*dt+(2+z)(t*dz+z*dt)=0,
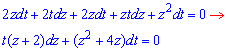
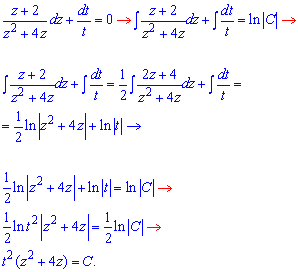
Повернемося до початкових змінних:
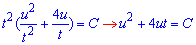
або u(u+4t)=C.
Оскільки t=x+3/4 і u=y-1/2, то (y-1/2)(y-1/2+4x+3)=C, або (2y-1)(8x+2y+5)=C - загальний інтеграл ДР.
Приклад 2.100 Знайти розв'язок диференціального рівняння
(1-2x-2y)dx+(3x+y-1)dy=0,
Розв'язання: Складаємо систему рівнянь і розв'язуємо її:
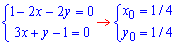
звідси
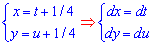 ,
,
маємо
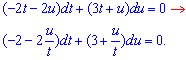
Робимо заміну u=z*t, тоді z=u/t, відповідно du=t*dz+z*dt,
(-2-2z)dt+(3+z)(t*dz+z*dt)=0,
t(3+z)dz+(z2+z-2)dt=0,
розділяємо змінні та інтегруємо диференціальне рівняння
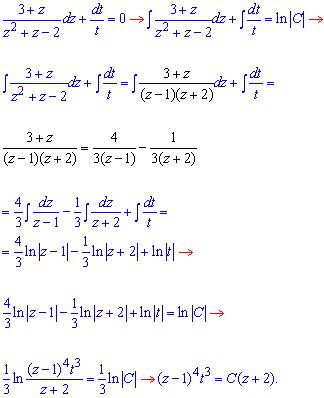
Повертаємося до початкової заміни:
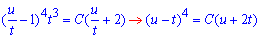
Оскільки t=x-1/4 і u=y-1/4, то (y-x)4=C(4y+8x-3).
Врахуємо, що z2+z-2=0 , z=1 і z=-2, тоді u=t, звідки x=y
(враховано при C=0)
u=-2t, звідки 4y+8x-3=0.
Тому (y-x)4=C(4y+8x-3) і (y-x)4=C(4y+8x-3) - загальні інтеграли рівняння.
Використана література:
- Збірник задач з курсу «Диференціальні рівняння». Бокало М. М. – Львів: Видавничий центр ЛНУ імені Івана Франка, 2014. – 179 с.
- Диференціальні рівняння. Бокало М. М. – Львів: Видавничий центр ЛНУ імені Івана Франка, 2014. – 232 с.
- Диференціальні рівняння в задачах: Навч. посібник / А. М. Самойленко, С. А. Кривошея, М. О. Перестюк. – К.: Либідь, 2003. – 504 с.
- Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление – 2-е изд. – Наука, 1969. – 424 стр. с илл.
Проте схема обчислень достатньо добре описана в підручниах та дає можливість знайти розв'язок ДР, хоч при цьому приходиться виконувати масу обчислень. Щоб не лякати Вас зразу перейдемо до аналізу готових відповідей з яких все стане зрозумілим.
Приклад 1 (3.11) Знайти загальний інтеграл диференціального рівняння
![]() Розв'язання: Перед нами зовсім інший тип диф. рівнянь ніж ті, що були розглянуті раніше. Схема обчислень теж відрізняється, спершу необхідно визначити стаціонарну точку - для цього маємо знайти нулі чисельника і знаменника.
Розв'язання: Перед нами зовсім інший тип диф. рівнянь ніж ті, що були розглянуті раніше. Схема обчислень теж відрізняється, спершу необхідно визначити стаціонарну точку - для цього маємо знайти нулі чисельника і знаменника.
Розв'яжемо систему рівнянь:
![]()
Стаціонарною точкою є М(-1;1).
Далі виконуємо заміну змінних (зміщення координат)
![]()
звідси вихідне ДР перетворимо до однорідного диференціального рівняння
![]() або
або ![]()
Виконаємо заміну змінних 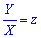 , та знаходимо диференціал через нову змінну
, та знаходимо диференціал через нову змінну
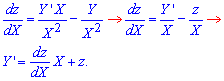
Підставляючи в рівняння, отримаємо просту для обчислень залежність
![]()
яку легко зводимо до рівняння з відокремленими змінними
![]()
Далі інтегруємо обидві частини
![]()
та знаходимо загальний розв'язок рівняння
![]()
Вертаючись до самої першої заміни, отримаємо
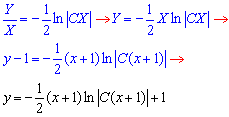
де 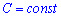 - довільна константа.
- довільна константа.
Ось в такому вигляді отримали загальний інтеграл диференціального рівняння. Добре розберіть наведену схему обчислень, вона для студентів на ціну золота.
Приклад 2 (3.17) Знайти загальний інтеграл диференціального рівняння
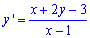 Розв'язання: Дане диференціальне рівняння має розв'язок, проте не кожен студент без шпаргалки чи методички може знайти відповідь самостійно.
Розв'язання: Дане диференціальне рівняння має розв'язок, проте не кожен студент без шпаргалки чи методички може знайти відповідь самостійно.
Методика зведення рівняння до однорідного полягає в наступних діях: знаходимо стаціонарну точку (нулі чисельника та знаменника дробу).
Для цього розв'язуємо систему лінійних рівнянь:
![]()
Далі вводимо заміну змінних
![]()
Одиниці справа є розв'язками системи рівнянь.
Наше початкове диф. рівняння в нових змінних матиме запис
![]()
Саме для цього і розв'язували систему рівнянь.
Далі необхідно виконати заміну:
![]() , тоді
, тоді ![]() .
.
Після заміни отримане ДР можемо звести до рівняння з відокремленими змінними
![]()
Інтегруванням обох частин
![]()
прийдемо спершу до логарифма
![]()
Експонуванням обох частин отримаємо залежність
![]()
Вертаючись до нашої заміни, отримаємо розв'язок в нових змінних
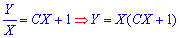
а далі остаточний інтеграл диференціального рівняння
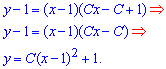
Де 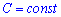 - довільна константа
- довільна константа
Ось так складно буває інколи отримати загальний розв'язок диференціального рівняння.
Приклад 3 (3.27) Розв'язати диференціальне рівняння
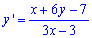 Розв'язання: Маємо ДР першого порядку, яке можна звести до однорідного диф. рівняння. Для цього знайдемо стаціонарну точку:
Розв'язання: Маємо ДР першого порядку, яке можна звести до однорідного диф. рівняння. Для цього знайдемо стаціонарну точку:
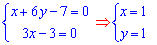
Маючи стаціонарну точку, виконуємо заміну координат
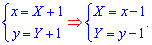 ,
,
Вихідне диференціальне рівняння перетвориться до вигляду
![]() або
або ![]()
Зробимо заміну змінних z=Y/X, Y=z*X, тоді похідна рівна
![]()
Підставимо її в рівняння та розділимо змінні, так отримаємо ДР з відокремленими змінними
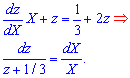
Інтегруємо диференціальне рівняння та приходимо до логарифмічного
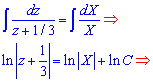
Експонуємо отриману залежність, попередньо звівши логарифми в правій частині за формулою добутку
![]() ,
,
Вертаючись до нашої заміни (z), отримаємо розв'язок
![]()
який після повторної заміни набуде зрозумілого вигляду
![]()
Перенісши одиницю вправо
![]()
отримаємо загальний розв'язок диференціального рівняння.
Тут розібрано лише 3 завдання, проте схему обчислень вони описують в повній мірі. Тепер Ви знаєте, що робити з рівняннями звідними до однорідних та після самостійної роботи з подібними прикладами не матимете труднощів на контрольних та екзаменах. Перегляньте наступні уроки, Вас чекає ще маса готових відповідей для вичення диференціальних рівнянь.
Приклад 1. Знайти загальний розв'язок лінійного однорідного диференціального рівняння другого порядку зі сталими коефіцієнтами.
а) y''-4y'+13y=0.
Обчислення: Розв'яжемо відповідне характеристичне (алгебраїчне) рівняння, ввівши заміну:
y(n)->k(n), де
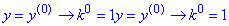
(Тобто порядок похідної функції y вказує на степінь змінної k).
Корені характеристичного рівняння обчислюємо через дискримінант
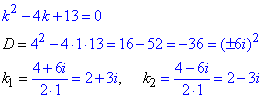
Оскільки корені є комплексними числами ( 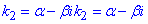 ), то розв'язок заданого диференціального рівняння записуємо у вигляді:
), то розв'язок заданого диференціального рівняння записуємо у вигляді: 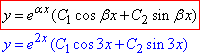
де C1 і C2 – довільні сталі.
б) y''+3y'-28y=0
Обчислення: Розв'яжемо відповідне характеристичне (алгебраїчне) рівняння, ввівши заміну:
y(n)->k(n) , де 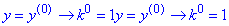
(Порядок похідної функції y вказує на степінь змінної k). Отже,
Через дискримінант отримаємо два різні корені
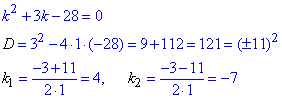
Оскільки корені характеристичного рівняння є різні дійсні числа (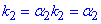 ), то розв'язок заданого диференціального рівняння записуємо у вигляді:
), то розв'язок заданого диференціального рівняння записуємо у вигляді:
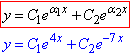
де C1 і C2 – довільні сталі.
в) Знайти частинний розв'язок лінійного однорідного диференціального рівняння другого порядку зі сталими коефіцієнтами.
36y''-60y'+25y=0, y(0)=5/6, y'(0)=25/36.
Обчислення:Складемо та обчислимо відповідне характеристичне (алгебраїчне) рівняння.
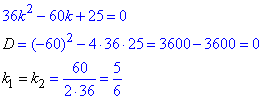
Бачимо, що корені характеристичного рівняння є однакові дійсні числа (k1=k2=α), тому загальний розв'язок диференціального рівняння записуємо у вигляді:
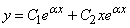 , тобто
, тобто
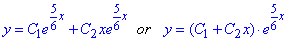
де C1, C2 – довільні сталі, які уточнюємо з умови Коші:
Підставимо початкові умови y(0)=5/6, y'(0)=25/36 у загальний розв'язок ДР:
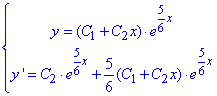
отримаємо
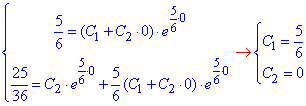
Підставлямо С1=5/6, С2=0 в "ігрик", звідси
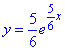 - частинний розв'язок рівняння.
- частинний розв'язок рівняння.
Тут розібрали варіанти, які найчастіше Вам задають на практичних. Більше готових відповідей на ДР можна переглянути на сусідніх сторінках сайту.
]]>