Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього оцінювання 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень при підготовці, систематизувати та підвищити накопичений рівень знань з математики. Рішення прикладів з математики будуть цікаві для школярів 9, 10, 11 класів, а також їх батьків.
Розділ 6. Стереометрія
Завдання 6. 1 - 6.21 мають по п'ять варіантів відповідей, із яких тільки одна правильна. Правильно виконане завдання оцінюється 1 балом.
Задача 6.4 Діагональ куба дорівнює 6 см. Знайдіть площу повної поверхні куба.
Розв'язання: Діагональ куба рівна стороні, помноженій на корінь з трьох. З цієї залежності визначаємо ребро куба
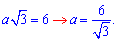
Куб має 6 граней, тобто площа рівна площам 6 квадратів зі знайденою стороною. Виконаємо обчислення
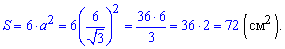
Площа поверхні куба рівна 72 сантиметри квадратні.
Відповідь: 72.
Задача 6.5 Обчисліть довжину меншої діагоналі прямої призми, в основі якої ромб із стороною 6 м та гострим кутом 60°. Висота призми 8 м.
Розв'язання: Виконаємо побудову до задачі
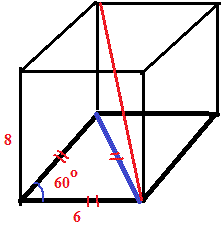
Менша діагональ ромба рівна також 6 м. Це випливає з того, що кути в трикутнику при діагоналі 60 градусів, а сам трикутник є рівностороннім. Тоді діагональ призми є гіпотенузою прямокутного трикутника зі сторонами 6 і 8 метрів. Знаходимо довжину гіпотенузи
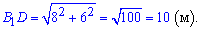
Варіант В містить правильну відповідь до тесту.
Відповідь: 10 м.
Задача 6.6 В основі прямої призми лежить рівнобічна трапеція з бічною стороною 5см та основами 4 і 10 см. Бічне ребро призми - 10 см. Обчисліть площу повної поверхні призми.
Розв'язання: Побудуємо призму, в основі якої трапеція
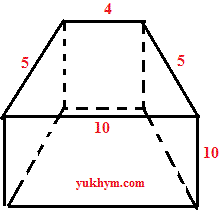Площа повної поверхні призми рівна подвійній площі трапеції + 4 прямокутники побудовані на сторонах трапеції з висотою призми. Намалюємо рівнобічну трапецію та знайдемо її висоту. Катет при основі прямокутного трикутника знаходимо як половину різниці основ трапеції
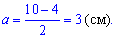
Далі знаходимо висоту трапеції, вона рівна катету трикутника
Знаходимо площу трапеції та бічної поверхні призми
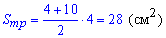
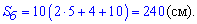
Далі за наведеною вище формулою знаходимо площу поверхні призми
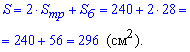
Знайдена площа відповідає варіанту А тестів.
Відповідь: А.
Допомога з математики у вигляді готових рішень полегшить навчання всіх школярів і буде гарною інструкцією на іспитах і тестах. Готові тестові приклади обов'язково стануть в нагоді у навчанні школярам в 9, 10, 11 класі. Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО 2017 відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Двогранні кути
- Наступна стаття - ЗНО 2017 математика. Знаходження об'єму фігур
