ЗНО математика. Площа фігури, обмежена графіком функцій

Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики у 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.

Розділ III. Функції

Завдання 3.1 - 3.45 мають по п'ять варіантів відповідей, із яких тільки одна правильна. Правильно виконане завдання оцінюється 1 балом.

Завдання 3.44 Укажіть формулу для обчислення площі фігури, обмеженої графіком функції у = х( х - 2) і віссю ОХ.

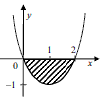
Розв'язання: Площа фігури обмежена двома ривки рівна інтегралу від різниці верхньої і нижньої кривої. В даному завданні потрібно знайти точки перетину функції з віссю абсцис. Для цього розв'яжемо рівняння
х( х - 2)=0;
x=0; x=2.
Знаючи точки перетину, а також, що верхня крива це вісь або 0, а нижня задана рівнянням параболи, обчислюємо площу з інтегралу
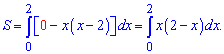
Площа
На початку інтегралу 0 означає віднімання від верхньої кривої, тобто осі абсцис. Ось тому, коли шукають площу між кривою, що вища осі і віссю Ох нулик пропускають. Але Ви про це повинні знати.
Отриманий інтеграл відповідає варіанту Б тестів.
Відповідь: Б.

Завдання 3.45 Укажіть формулу для обчислення площі фігури, обмеженої графіками функцій у = х² та у = -х² + 4x.

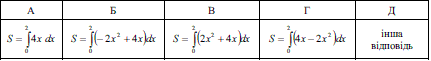
Розв'язання: Спершу знайдемо точки перетину графіків функцій. Для цього прирівняємо їх рівняння
х²=-х² + 4x;
2х²-4x=0;
2x*(x-2)=0;
x=0; x=2.
Графік функцій та затушована площа між кривими наведені нижче
графік дотичної
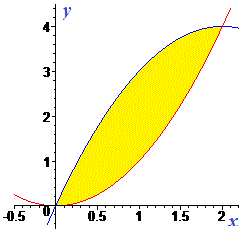
Потрібно знати, що верхня крива при "ікс" в квадраті має від'ємний знак.
Тоді площа між кривими рівна інтегралу

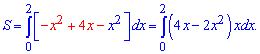
Отримана формула площі відповідає варіанту Г тестових відповідей.
Відповідь: Г.