Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики у 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.
Розділ III. Функції
В завданнях 3.46 - 3.62 правильна відповідь оцінюється 2 балами.
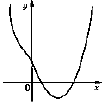Завдання 3.46 (Т-06, 31) На рисунку зображено графік функції f(x)=x4-x2+b*x+с. Визначте знаки параметрів b і с. У відповіді вкажіть номер правильного варіанта з наведених нижче.
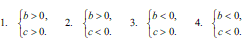
Розв'язання: Є декілька способів вирішення даного завдання. Константа C відповідає за значення функції в нулі. З рисунку бачимо, що вона приймає додатне значення. Далі потрібно визначити параметр b. Для цього є кілька шляхів. Відомо, що при малих значеннях від 0 і до 1 найбільший вклад в графік функції (границі) мають наймолодші члени. Тому з побудови бачимо, що після 0 функція спадає, отже похідна від'ємна. Другий метод полягає в обчисленні похідної
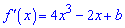
Оскільки в нулі функція спадає, то похідна в нулі має бути менша нуля
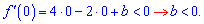
На основі аналізу робимо висновок, що третій варіант відповідей є правильним.
Відповідь: 3.
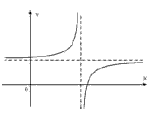Завдання 3.47 За ескізом графіка функції у=(a*x+b)/(x+c) визначіть знаки параметрів а ,b, c. У відповіді вкажіть номер правильного варіанта з наведених нижче.
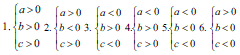
Розв'язання: Задана дробова функція, яка містить вільний член як в чисельнику так і знаменнику. Щоб визначити невідної розпочнемо аналіз з розгляду асимптот функції.
З графіка бачимо, що функція має вертикальну і горизонтальну асимптоти при додатних значеннях аргументу та ординати. Вертикальна асимптота має місце коли знаменник дробу рівний 0. З цієї умови визначаємо знак невідомої
x+c=0; x=-c>0; c<0.
Горизонтальна асимптота рівна границі при змінній, що прямує до безмежності. Для наведеної функції границя рівна a>0.
Невідому, що залишилася визначаємо з умови, що функція в нулі приймає додатне значення
b/c>0.
Оскільки c<0 то попередня умова може виконуватися, якщо b<0. З відповідей до ЗНО тестів з математики потрібно вибрати варіант, який містить такий комплект знаків невідомих
a>0; b<0; c<0.
Таким є 6 варіант.
Відповідь: 6.
Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО 2017 відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Площа фігури, обмежена графіком
- Наступна стаття - ЗНО 2017 математика. Аналіз функції за графіком
