Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики у 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.
Розділ III. Функції
Завдання 3.1 - 3.45 мають по п'ять варіантів відповідей, із яких тільки одна правильна. Правильно виконане завдання оцінюється 1 балом.
Завдання 3.13 Задано функції:
1) у = х - 2; 2)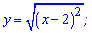 3)
3) 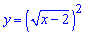
Укажіть правильне твердження.

Розв'язання: Дане завдання ми рекомендуємо задавати на будь яких тестах. За результатами тестування зразу можна сказати, хто добре знає тему «Функції», а хто не дуже. Перша функція пряма, тому функція визначена всюди
y=x-2.
Друга може бути записана у вигляді y=|x-2| - це модуль функція.
Остання корінь функція в квадраті, тому областю визначення є всі значення при яких підкоренева функція невід'ємна. ЇЇ можна перетворити до вигляду
y=x-2 – визначена для 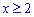 .
.
Звідси робимо висновок, що графіки наведених функцій різні.
Відповідь: Д.
Завдання 3.14 (Т-06, 28) Укажіть непарну функцію.
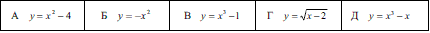
Розв'язання: Непарною є така функція, яка при від'ємному аргументі рівна протилежному за знаком значенню. Перевіримо кожну із тестових відповідей
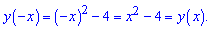
Перша функція парна. Перевіримо наступну
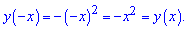
Вона теж парна, про це можна було здогадатися за парністю степенів при аргументі. Третя функція коренева і змінна під коренем знаходиться в непарному степені, отже функція ні парна ні непарна. Можна це і не розписувати. Залишилося перевірити останню функцію
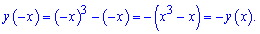
Бачимо, що вона непарна. Отже варіант Д тестів є правильним.
Відповідь: Д.
Завдання 3.15 (Т-07, 63) Укажіть парну функцію.
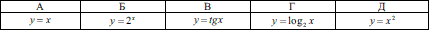
Розв'язання: Серед наведених в відповідях до тестів функцій шукаємо з аргументом в парному степені. Для наочності розпишемо останню
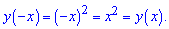
Отже варіант Д тестів може добавити 1 бал, якщо Ви його визначите.
Відповідь: Д.
Завдання 3.16 Укажіть непарну функцію, областю значень якої є проміжок [-1;1].
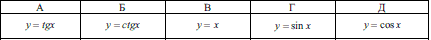
Розв'язання: Тангенс і котангенс хоча є непарними функціями, проте їх область значень набагато ширша за наведений проміжок. Те ж саме стосується прямої – варіант В тестів. Далі йде синус і косинус, які точно мають областю значень проміжок [-1;1], однак косинус є парною функцією, тому його відкидаємо з відповідей. І лише синус функція задовольняє умову прикладу, тобто – варіант Г тестів.
Відповідь: Г.
Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО 2017 відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Аналіз графіку функції
- Наступна стаття - ЗНО 2017 математика. Максимуми і мінімуми


