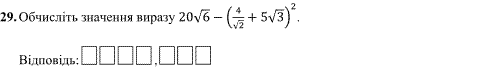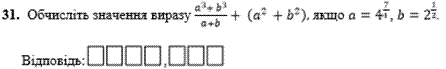Продовжуємо аналізувати розв'язки завдань зовнішнього незалежного оцінювання за 2015 рік з математики.
В попередній статті були наведені відповіді пробного ЗНО до завдань № 1-24, які під силу виконати усім школярам.
Останні задачі більш складні та вимагають добрих теоретичних знань з математики.
Розбір розв'язків є актуальним не тільки для абітурієнтів, які шукають можливості поступити у ВУЗи та здобути вищу освіту, а й для студентів, які вже проходили тестування.
Завдання 25
1. Позначимо швидкість пішохода через V, тоді швидкість велосипедиста (за умовою) рівна V+12.
Відомо, що відстань рівна швидкості помноженій на час руху.
Щоб скласти рівняння прирівнюємо відстані S=V*t пройдені пішоходом та велосипедистом
2(V+12)=6V;
2V+24=6V;
4V=24;
V=24/4=6 км/год.
Знайдемо відстань між містами
S=6*6=36 км.
2. Обчислимо швидкість велосипедиста
V+12= 6+12=18 км/год.
Час за який пішохід та велосипедист зустрінуться знайдемо з рівняння
6•t+18•t=36;
24t=36;
t=36/24=1,5 год.
Ось так повинні виглядати пояснення до задачі на швидкість і рух.
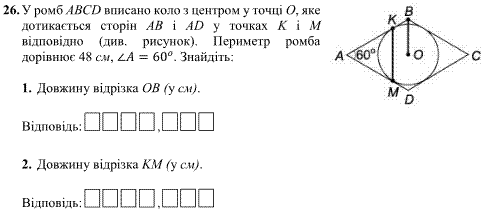
Завдання 26
Задачі на ромб не завжди складні, і в цьому Ви зараз переконаєтеся.
Знайдемо, довжину OB, як половину меншої діагоналі. За властивістю ромба діагоналі є бісектрисами кутів, тому кут
< AOB=60/2=30.
Трикутник AOB прямокутний, тому сторона навпроти кута 30 градусів рівний половині гіпотенузи, а вона в свою чергу рівна четвертині периметра.
Звідси OB=48/2/4=6 см.
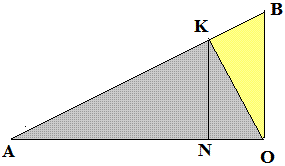
Щоб знайти KM виконаємо додаткову побудову.
За рисунком KM=2*KN.
Знайдемо сторону OA прямокутного трикутника AOB за теоремою Піфагора. 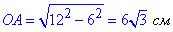
Далі знайдемо OK з формули площі, далі KB за Піфагором, KA та KN зі співвідношень на площу. 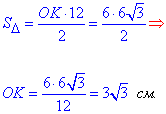
З прямокутного трикутника OKB за теоремою Піфагора знаходимо катет KB. 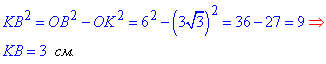
AK=AB-KB=12-3=9 см.
Далі за формулою площі через висоту складаємо залежність для знаходження KN
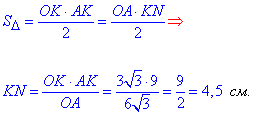
KM в два рази більша KN
KM=2*4,5=9 см.
Завдання 27
Завдання на складання рівнянь.
Тут слід зауважити, що номерація починається не з нуля, а з одиниці.
Саме на цьому багато абітурієнтів зробили помилки
S4=a1+(4-1)*d=142;
S7=a1+(7-1)*d=154.
Від другого рівняння віднімемо перше, в результаті отримаємо
3d=154-142=12;
d=12/3=4 (грн).
Далі визначаємо вартість доставки великогабаритних меблів на перший поверх
a1+3*4=142;
a1=142-12=130.
Далі знаходимо вартість доставки меблів на 11 поверх
S11=130+(11-1)*4=130+40=170 (грн).
Це і є правильна відповідь до ЗНО тестів за 2015 рік.
Завдання 28
Розкриття логарифмічної нерівності розпочнемо з області визначеня логарифма, від має приймати додатні аргументи, звідси
2x-3>0;
x>1.5
Розкриємо логарифм проекспонувавши обидві частини нерівності
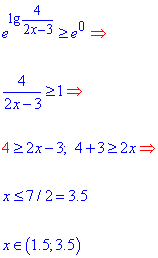
Найбільше значення змінної, що задовольняє логарифмічну нерівність рівне 3,5.
Завдання 29
Спростимо вираз, піднісши дужку з коренями до квадрату 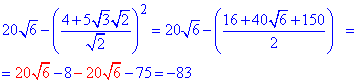
В результаті спрощення ірраціонального виразу отримаємо -83.
Завдання 30

В основі маємо круг, тому правильніше було сказати, що діаметр в основі рівний 16 см.
Тоді радіус рівний 16/2=8 см.
Відомо, що об'єм конуса визначається за формулою
V=Pi*R^2*h/3.
При підстановці відомих величин отримаємо рівняння на висоту конуса
Pi*8^2*h/3=320*Pi.
Звідси
h=3*320/64=15 см.
Маючи радіус основи та висоту конуса, бічну сторону знаходимо як гіпотенузу прямокутного трикутника
L=sqrt(15^2+8^2)=sqrt(289)=17 см.
Це і є правильна відповідь до ЗНО тестів.
Завдання 31
Тут дріб не вдасться спростити за формулами скороченого множення, тому Виконуємо підстановку та спрощення кожного з доданків.
Знайдемо суму квадратів параметрів
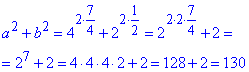
Далі розпишемо другий доданок
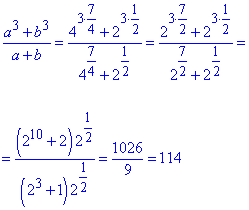
Обчислюємо суму виразів
114+130=244
Завдання 32
Надіюсь, щояснення будуть зрозумілі для школярів, тому що завдання певною мірою зачіпає основи теорії ймовірності.
За правилами комбінаторики лінійку і транспортир можна вибрати 3*4=12 варіантами, і ще 2 за готовими наборами.
Тому сумарно маємо
12+2=14
Завдання 33
Щоб краще зрозуміти задачу слід розібратися, що собою являє правильна чотирикутна піраміда.
Правильна означає, що в основі лежить квадрат. Для кращого розуміння, як використати кут між гранню та основою виконаємо допоміжну побудову
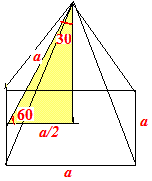
Кут при основі 60 градусів. Звідси при вершині він рівний 30 градусів.
Позначимо висоту бічної грані через a, тоді пів основи навпроти кута 30 градусів рівна половині, а састорони основи =a.
Через висоту бічної грані знаходимо площу 4 граней та основи як квадрату.
За мовою сума рівна 54 на корінь з 6.
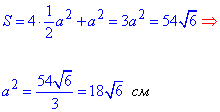
Звідси знаходимо a^2.
Щоб знайти площу необхідного перерізу знайдемо висоту піраміди та діагональ квадрату, що є в її основі
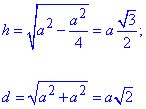
Знаючи їх знаходимо площу трикутника за формулою.
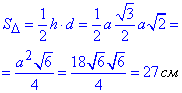
Квадрат сторони раніше знайдений, він і є ключем до розв'язку задачі.
Завдання 34
Дослідимо функцію y=x^4-8x^2+C на екстремум.
Він досягається або в критичних точках або на краях проміжку [-1;3].
Знайдемо похідну функції та прирівняємо її до нуля
y'=4x^3-8*2x=0;
4x(x^2-4)=0.
x=0, x=-2,x =2.
Знайдемо значення функції на краях та в двох точках локального ектремуму
y(-1)=1-8+C=-7+C;
y(0)=C;
y(2)=2^4-8*2^2+C=-16+C;
y(3)=3^4-8*3^2+C=-9+C.
Найменше з наведених значень досягається в точці x=2.
З початкової умови, що в точці мінімуму функція рівна 30 визначаємо параметр С.
30=y(2)=-16+C;
C=30+16=46.
Завдання 35
Дане завдання скоріш за все містить опечатку, оскільки без задання сторони CD може приймати будь-які розміри.
Хто має відповідь до завданння просьба поділитися з нами, нам дуже цікаво як школярі могли виконати дане завдання!
Завдання 36
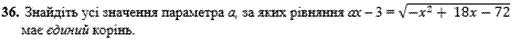
Задача на знаходження параметра. В правій стороні маємо корінь, в лівій функцію з параметром, яка взагалі може приймати відємні значення. Тому при розкритті ірраціональності (піднесенні до квадрату) можуть виникнути корені, які не задовольняють рівняння. Тому спершу знаходимо розвязки, а далі виконуємо перевірку їх коректності.
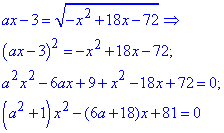
В результаті прийдемо до квадратного рівняння.
Щоб рівняння мало єдиний корінь необхідно, щоб дискримінант дорівнював нулю. З цієї умови знаходимо значення невідомих параметрів
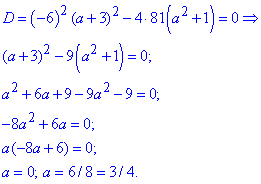
Отримали два параметри, проте підстановка показує, що значення a=0 не є розв'язком, оскільки a•x-3=-3, а права сторона рівна кореню, який завжди додатній.
Тому існує лише один параметр за якого рівняння має єдиний розв'язок і він рівний
a=3/4=0.75
Думаю, наведені пояснення до пробного ЗНО 2015 року з математики стануть добрим репетитором для Вас при підготовці до тестів.
Щоб допомогти всім випускникам шкіл краще підготуватися до незалежного тестування просимо максимально поширити ппосилання на готові відповіді в соціальних мережах.