Розв'язки завдань зовнішнього тестування з математики стане в нагоді при підготовці до тестувань. Відповіді на завдання 17-22 не надто складні і після аналізу Вами внесуть суттєвий вклад в підготовку до ЗНО.
------------------------------
Завдання 17. Спростіть вираз
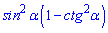
Варіанти відповідей:
А) 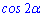
Б) 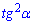
В) 1
Г) 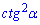
Д) 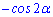
Розв'язання: Перетворимо вираз у дужках
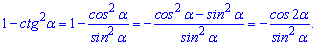
та спростимо
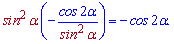
Без знання перетворень тригонометричних виразів подібні завдання не завжди легко вдається спростити, тому постарайтеся при підготовці до ЗНО або іншого тестування вивчити хоча б базові перетворення.
Відповідь: Д.
------------------------------
Завдання 18. Знайдіть похідну функцію 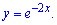
Варіанти відповідей:
А) 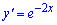
Б) 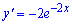
В) 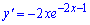
Г) 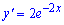
Д) 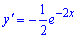
Розв'язання: За правилом диференціювання складної функції знаходимо
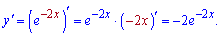
Відповідь: Б.
------------------------------
Завдання 19. Розв'яжіть нерівність
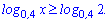
Варіанти відповідей:
А) 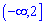
Б) 
В) 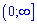
Г) 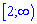
Д) 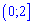
Розв'язання: Оскільки основи однакові, то проекспонуємо обидві частини нерівності, пам'ятаючи при цьому важливе правило: якщо основа менша одиниці то знак нерівності міняється на протилежний
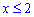
Так як ОДЗ логарифма починається від нуля і при від'ємних значеннях він не існує то розв'язком буде проміжок
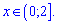
Відповідь: Д.
------------------------------
Завдання 20. Для розігрівання в мікрохвильовій печі рідких страв використовують посудину у форму циліндра, радіус основи якого дорівнює 9 см. Посудина ставиться на горизонтальний диск у формі круга і накривається кришкою, що має форму півсфери (див. рисунок). Радіус півсфери дорівнює 12 см і є меншим за радіус круга. Укажіть найбільше з наведених значень, якому може дорівнювати висота посудини, якщо посудина не торкається кришки.
Варіанти відповідей:
А) 3 см
Б) 5 см
В) 6 см
Г) 7 см
Д) 8 см
Розв'язання: Завдання достатньо каверзнеі багато хто з Вас за нього не брався. Висоту посудини можна знайти, застосувавши теорему Піфагора до прямокутного трикутника з гіпотенузою, яка рівна радіусу півсфери і катетами, які рівні висоті і радіусу основи посудини.
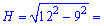
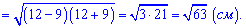
Найближче ціле значення знаходимо з наступних міркувань
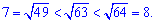
Таким чином, якщо посудина не торкається кришки, то її максимальна ціла висота рівна 7 см.
Відповідь: Г.
------------------------------
Завдання 21. З пунктів А і В одночасно по шосе назустріч один одному виїхали два велосипедисти. Вони їхали без зупинок із сталими швидкостями: перший – зі швидкістю х км/год, другий – зі швидкістю у км/год (x>y). Через t годин (t>1) вони зустрілися в точці С і , не зупиняючись, продовжили рух буз зміни напрямків.
1. На скільки кілометрів зменшилася відстань по шосе між велосипедистами через 1 годину після початку руху?
2. Чому дорівнює відстань по шосе між пунктами А і В (у км).
3. На скільки кілометрів більше проїхав перший велосипедист, ніж другий, за час від початку руху до моменту зустрічі?
4. За скільки годин перший велосипедист подолає відстань по шосе від точки С до пунку В?
Варіанти відповідей:
А) 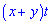
Б) 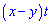
В) 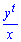
Г) 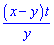
Д) 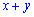
Розв'язання:
1. За першу годину перший велосипедист проїхав 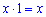 км, а другий відповідно
км, а другий відповідно 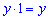 км.
км.
Просумувавши отримаємо, 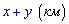 що відстань між велосипедистами зменшилась на
що відстань між велосипедистами зменшилась на  км, тобто варіант Д.
км, тобто варіант Д.
2. Відстань від пункту А до місця зустрічі рівна 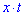 км, і від пункту В до цього ж місця
км, і від пункту В до цього ж місця 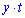 км. Додавши ці проміжки ми знайдемо відстань від А до В,
км. Додавши ці проміжки ми знайдемо відстань від А до В,
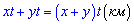
або варіант А.
3. Оскільки швидкості велосипедистів постійні і першого більша на х-у км/год порівняно з другим, то за час 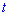 він поїхав
він поїхав 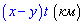
більше від старту до моменту зустрічі. Значенню відповідає варіант Б.
4. Відстань від пункту В до точки зустрічі рівна yt км. Перший велосипедист їде зі швидкістю х км/год. Щоб знайти час в дорозі першого велосипедиста потрібно відстань розділити на швидкість, тобто за
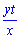
годин перший велосипедист прибуде до пункту зустрічі, або варіант В.
Відповідь: 1-Д); 2-А);3-Б); 4-В).
------------------------------
Завдання 22. Установіть відповідність між твердженням (1-4) та функцією (А-Д), для якої це твердження є правильним.
Твердження
1. графік функції не перетинає жодну з осей координат
2. областю значень функції є проміжок 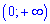
3. функція спадає на свій області визначення
4. на відрізку [-1,5;1,5] функція має два нулі
Варіанти відповідей:
А) 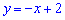
Б) 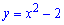
В) 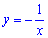
Г) 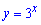
Д) 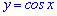
Розв'язання: Для відповіді на вказані питання потрібно провести аналіз на кожне твердження функцій і вияснити для яких вони справедливі. Ми ж наведемо правильні відповіді відкидаючи зайві подробиці.
1. Графік функції 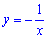 не перетинає осі координат оскільки ОДЗ виключає точку х=0 і відповідно не знайдеться точки при якій ордината буде рівна нулю y=0.
не перетинає осі координат оскільки ОДЗ виключає точку х=0 і відповідно не знайдеться точки при якій ордината буде рівна нулю y=0.
2. Областю значень степеневої функції 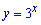 є проміжок
є проміжок 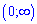 . Це повинні знати усі школярі.
. Це повинні знати усі школярі.
3. Функція 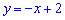 спадає на всій області визначення. В цьому легко переконатися знайшовши першу похідну
спадає на всій області визначення. В цьому легко переконатися знайшовши першу похідну 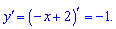
Вона менша нуля, отже функція y спадна.
4. Функція 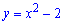 має два корені (нулі) на проміжку [-1,5;1,5].
має два корені (нулі) на проміжку [-1,5;1,5].
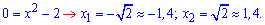
Підсумовуючи все вище сказана, отримаємо кінцевий результат розв'язування завдання.
Відповідь: 1-В); 2-Г) 3-А); 4-Б).
------------------------------
Переглянути відповіді завдань № 11-16 ЗНО-2013 математика та відповідь до завдань № 23-28 ЗНО-2013 математика


