Продовжуємо детальний аналіз відповідей до ЗНО 2016 р. з математики.
Сьогодні залишилося розібрати 7 завдань, які принесуть чимало балів при тестуванні.
Читайте готові відповіді до ЗНО та діліться матеріалом з друзями.
Завдання 26

1. Щоб краще усвідомити, що від Вас чекають виконаємо допоміжний рисунок трикутника.
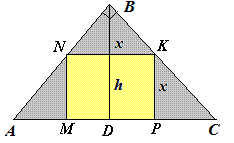
Оскільки маємо прямий кут та рівнобедрений трикутник, то його висота рівна половині гіпотенузи.
h=3,6/2=1,8.
Далі за основою та висотою знаходимо площу трикутника ABC
S=1,8•3,6/2=3,24
2. Щоб знайти пощу квадрата спершу треба обчислити його сторону.
Для цього є кілька способів, найлегший з пропорцій.
Позначимо сторону квадрату через х.
Трикутники BDC та KPC подібні.
Звідси складаємо пропорції
BD/DC=KP/PC;
1,8/1,8=x/(1,8-x);
x=1,8-x;
2x=1,8;
x=1,8/2=0,9 м.
Знаходимо площу квадрата
S=0,9^2=0,81 м^2.
Відповідь: 1) 3,24; 2) 0,81.
Завдання 27

Задача на суму арифметичної прогресії.
Першого дня студент розв'язав 11 задач, другого 11+d, 9 дня- 11+8d.
Cума прогресії 315.
З формули суми визначимо крок прогресії
S=(a1+a9)*9/2 (11+11+8*d)*9/2=315;
11*9+4*9*d=315;
36d=315-99=216;
d=216/36=6.
Крок прогресії ми знайшли, за формулою знаходимо скільки задач студент розв'язав 9 дня a9=11+8*d=11+8*6=59.
Відповідь: 59.
Завдання 28
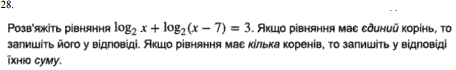
Логарифмічні рівняння мало хто з школярів любить обчислювати, проте в них нічого скадного немає.
В даному завданні та подібних хитрість полягає в тому, що рівняння має два корені, один з яких відємний.
Проте рідко хто перевіряє область визначення логарифма, а вона відповідає всім значенням аргумента більшим за нуль.
Запишемо рівняння у вигляді
log2x+log2(x-7)=3•log22;
log2x(x-7)=log22^3;
x(x-7)=2^3=8;
x^2-7x-8=0.
Корені квадратного рівняння за теоремою Вієта рівні x=-1; x=8.
Перший выдкидаємо, оскільки він не належить ОДЗ.
Єдиний розвязок логарифмічного рівняння x=8.
І не лякайтеся умови: «якщо рівняння має кілька коренів, то знайдіть їх суму».
Це більше психологічний тиск, аніж заклик до помилок.
Відповідь: 8.
Завдання 29

Задачі на формули комбінаторики.
Оскільки нас не цікавить яким за порядком в нас буде в букеті кожен нарцис чи тюльпан, то існує
9•8•7/(3•2•1)
способів вибору 3 нарцисів та
4•3/(2•1)
способи вибору тюльпанів.
Сумарна кількість способів скласти букет рівна їх добутку.
Загалом отримаємо
9•8•7/(3•2•1)•4•3/(2•1)=504
способів вибору букета.
Відповідь: 504.
Завдання 30
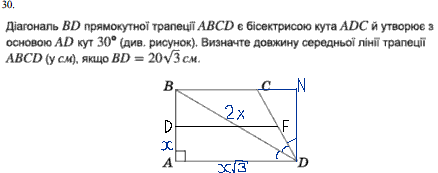
Нехай середня лінія трапеції DF.
Відомо, що катет навпроти кута 30 градусів в прямокутному трикутнику рівний половині гіпотенузи.
Позначимо діагональ трапеції BD через 2x, тоді AB=x.
Основа AD рівна за теоремою Піфагора x√3 або
AD=BD/2•√3=20•√3•√3/2=30 см.
Для обчислення BC виконаэмо добудову трапецыъ до прямокутника ABND.
З точки D маємо три кути по 30 градусів.
Звідси
СD=2y,
CN=y,
ND=y√3.
Так як AB=ND, то y√3=10√3, звідси CN=y=10.
Знайдемо другу основу трапеції
BC=30-10=20 см.
Обчислимо середню лінію трапеції
DF=(AD+BC)/2=(30+20)/2=25 см.
Відповідь: 25.
Завдання 31

Завдання не з легких і полягає в пошуку локальних екстремумів через похідну. Продиференціюємо функцію та прирівняємо похідну до нуля
f'(x)=1+2cos(2x)=0;
cos(2x)=-1/2;
2x=90+30=120;
x=120/2=60.
Кут належить досліджуваному інтервалу.
В цій точці досягається максимум
f(max)=Pi/3+sin(2•Pi/3)=Pi/3+√3/2=1,9132.
Мінімум досягається в нулі, це легко вгадати з аналізу обох складових функції
f(min)=0+0=0.
Графік заданої функції разом з колом для визначення косинуса зображено на рисунку
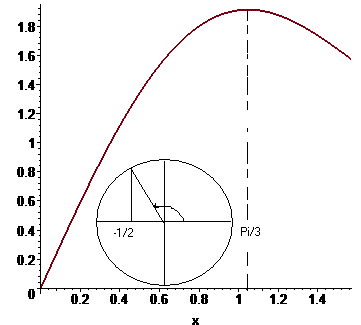
Завдання 33

Розв'язок 33 завдання до пробного ЗНО 2016 року кортко має вигляд. 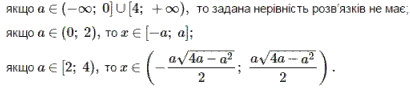
Більш детально аналіз можна побачити з наступного відео.
Сподобалися відповіді до ЗНО з математики, тоді діліться посиланням серед школярів!


