Завдання та відповіді до пробного ЗНО з математики за 2016 рік допоможуть Вам при підготовці до тестів.
Більшість завдань добре обгрунтована, що дозволяє не тільки побачити правильну відповідь, а й навчитися обчислювати задачі.
Плюсом всього матеріалу є те, що Вам не потрібно нічого завантажувати, лайкати, скачувати чи клікати по рекламі.
Просто з ноутбуків чи смартфонів заходите і у вільний від навчання час аналізуєте відповіді до ЗНО з математики.
Завдання 1
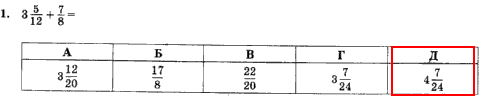
Виконуємо спрощення, для цього вносимо дроби під спільний знаменник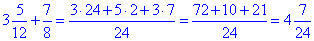
Вкінці навпаки виконуємо ділення націло та знаходимо остачу.
Завдання 2

Завдання на периметр паралелограма одне з найлегших, що нам доводилося вирішувати
BC=(60-2*10)/2=20 см.
Побільше б таких прикладів для школярів на ЗНО.
Завдання 3

З пропорції визначаємо загальну кількість
4x+5x=9x.
Загальна кількість кульок повинна націло ділитися на 9.
При діленні 100 на 9 в остачі отримаємо одиницю,
115 при діленні на 9 дасть в остачі 7.
Число 117 ділеться на 9 без остачі
117:9=13.
Оскільки кожне завдання містить лише одну правильну відповідь, то наступниі числа немає змісту перевіряти.
Завдання 4

Маємо завдання на показникові рівняння. Розпишемо 125 як 5 в кубі.
Далі за умови що рівні основи прирівнюємо показники
5^(x+1)=125=5^3;
x+1=3;
x=3-1=2.
Варіант А) є відповіддю до завдань ЗНО тестів за 2016 рік.
Завдання 5
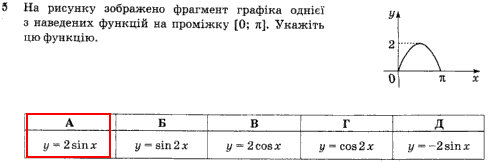
Маємо завдання на знання тригонометричних функцій.
Оскільки максимум рівний двійці то перед функцією повинен бути множник двійка.
Синус нуля нуль , в Pi синус теж=0, отже зображена функція відповідає
y=2sin(x).
Відповідь: А).
Завдання 6

Через точку можна провести безліч площин, які будуть паралельні до прямої і не проходитимуть через неї.
Тому правильна відповідь Д).
Завдання 7
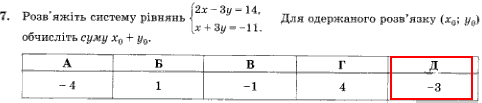
Система лінійних рівнянь досить вдало підібрана.
Просумуємо обидва рівняння щоб позбутися змінної «ігрик».
В результаті отримаємо
2x+x=14-11=3;
3x=3;
x=3/3=1.
Підставимо знайдене значення в друге рівняння
1+3y=-11;
3y=-11-1=-12;
y=-12/3=-4;
Сума розв'язків нерівності рівна
x+y=-4+1=-3.
Відповідь: Д).
Завдання 8

Число 12506975 має 8 цифр, дві з яких 5.
Тому ймовірність, що буде видалена п'ятірка рівна
p=2/8=1/4.
Відповідь: Д).
Завдання 9
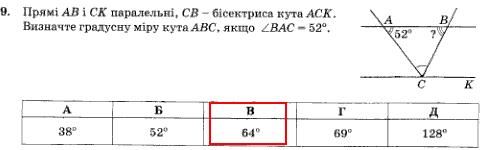
Якщо СB є бісектрисою кута BCK і виконується решта умов задачі, то кути ACB, CBA рівні.
Звідси маємо рівнобедрений трикутник, і знаходимо кут при основі через відомий кут при вершині
(180-52)/2=64 (градуси)
Відповідь: B).
Завдання 10
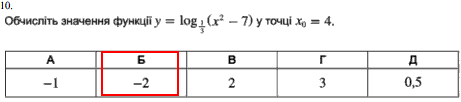
Для спрощення логарифма потрібно добре знати його властивості.
В даному завданні є декілька варіантів оформлення відповіді, зокрема наступний
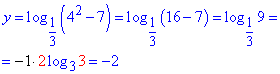
Відповідь: Б).
Завдання 11
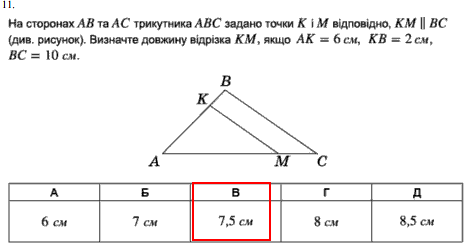
Завдання на пропорційні відрізки.
Трикутники ABC та AKM подібні.
Можна записати співвідношення
BC/AB =KM/AK.
Знайдемо
AB AB=6+2=8.
Обчислимо
KM KM=BC*AK/AB=10*6/8=7,5 см.
Така відповідь міститься в пункті В) тестів.
Завдання 12
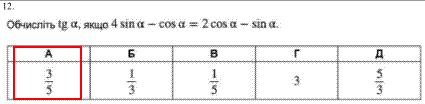
Завдання тільки на вигляд складне, загалом його вирішення полягає в розділення всього виразу на косинус. Це не змінить рівності, особливо якщо допускаємо, що косинус відмінний від нуля. В результаті отримаємо
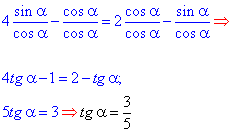
Відповідь: А.
Завдання 13
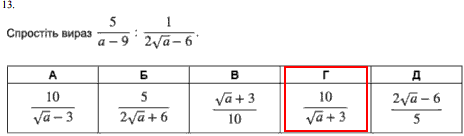
Завдання на спрощення дробів, поділити означає помножити на обернений вираз. Далі виділяємо спільним множником двійку, та щоб спростити корінь в чисельнику домножуємо на спряжений вираз. Результат зведення до відповіді наведено в формулі 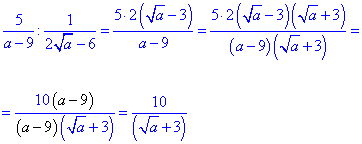
Відповідь: Г)
Завдання 14

Висоту призми знайдемо через діагональ та основу за теоремою Піфагора
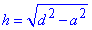
Далі площа бічної поверхні рівна 3 прямокутникам зі сторонами h,a.
Формула площі бічної поверхні
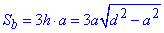
Відповідь: А)
Завдання 15
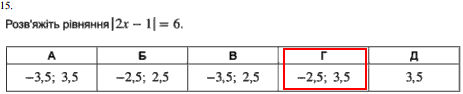
Розкриємо модулі в рівнянні, для цього спершу визначимо нуль підмодульної функції.
2x-1=0;
x=1/2.
При x>1/2 розкриваємо модуль
2x-1=6;
2x=7;
x=7/2=3,5.
При аргументах менших за 1/2 під модульна функція відємна, тому при розкритті модуля або перед функцією міняємо знак або праву сторону записуємо зі знаком мінус, тобто
-(2x-1)=6
2x-1=-6;
2x=-6+1=-5;
х=-5/2=-2,5.
Маємо два корені -2,5; 3,5.
Відповідь: Г)
Завдання 16

I. Ознака f(-10)=-f(10) вказує непарність функції, тому твердження не підходить для досліджуваної ф-ї.
II. Функція f(-6)=f(6) парна.
III. Симетрична відносно осі Oy функція є парною.
Відповідь: ІІ, ІІІ. Г)
Завдання 17

Обєм конуса визначаємо за формулою
V=1/3Pi*r^2*h.
Враховуючи, що об'єм сантиметра кубічного шоколаду рівний 3 грами отримаємо
M=3/3*3,14*1^2*3*100=942 грами.
Відповідь: Б).
Завдання 18
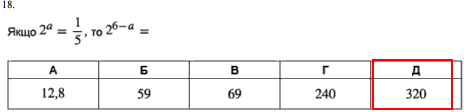
Розпишемо показникову залежнысть за правилом
2^(6-a)=2^6/2^a=64/(1/5)=64*5=320
Відповідь: Д)
Завдання 19

Завдання на первісну достатньо легке.
Сталу 1/2 можна винести за дужки, таким чином первісна для 1/x дасть ln|x|.
F(x)=1/2*ln|x|
Відповідь: Б)
Завдання 20

Розкриваємо дробову нерівність.
Оскільки вона нестрога, то чисельник може дорівнювати нулю.
Крім того в чисельнику маємо степінь=2, тому при переході через x=5 функція не змінює знаку.
Знайдемо нулі знаменника
x^2+x-6=(x+3)(x-2).
Звідси x=-3; x=2 та x=0 з чисельника.
Для перевірки знаку підставимо x=0.
Отримаэмо знак мінус, тому відповіддю є проміжки поза межами коренів квадратного рівняння
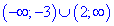
Відповідь: В)
Завдання 21

1. Графік функції y=5-x, має відємний кутовий коефіцієнт k=-1.
Тому утворює з додатним напрямом осі x тупий кут. В)
2. Графік функції y=2x+3 проходить через точку (-1,5;0), яка є внутрішньою для кола x^2+y^2=4.
Тому перетинає його в двох точка, оскільки перетинає його, а не дотикається. Д)
3. Графік функції 2x+6=0 це вертикальна пряма x=-6/2=-3, а тому не перетинає вісь y. A)
4. Графік функції y=x-4 можна записати у вигляді y-x=-4.
Він є пропорційним до прямої y-x=0, тому паралельний до неї. Г)
Завдання 22

Спростимо показникові вирази
1. 16^(1/2)=4^(2*1/2)=4;
2. (1/4)^(-2)=4^2=16;
3. (2^3)^2=2^(3*2)=2^6=64;
4. 2^3,5*2^1,5=2^(3,5+1,5)=2^5=32.
Думаю цих пояснень Вам достатньо, щоб знати як працювати з показниками на ЗНО.
Відповідь: 1 А), 2 В), 3 Д), 4 Г).
Завдання 23
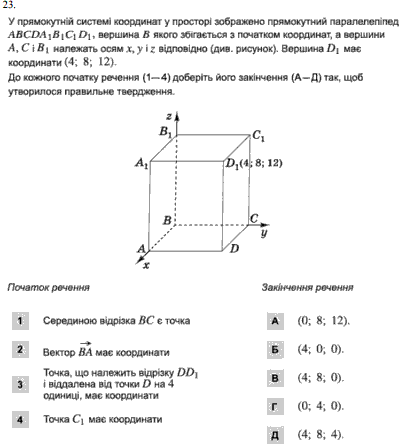
1. Відрізок BC лежить на осі Oy тому координати x=0, y=0.
Серединою відрізка є точка (0; 8/2;0)=(0;4;0)
2. Вектор ВА лежить на осі Ox, тому його координати (4;0;0).
3. Описана точка буде мати координати (4;8;4).
4. У точки С1 відсутня координата x, тобто (0;8;12).
Відповідь: 1 Г), 2 Б), 3 Д), 4 А).
Завдання 24
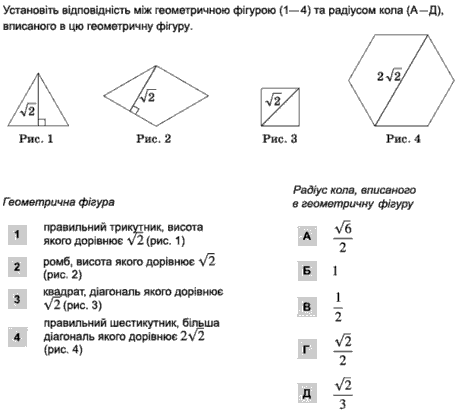
Тут немає чого довго розписувати, завдання на знання формул характеристик геометричних фігур - трикутника, ромба, многокутника.
Відповідь: 1 Д), 2 Г), 3 В), 4 А).
Завдання 25

1. Якщо дитячого взуття пошито 100% то жіночого 5•100%=500%.
Різниця рівна
500-100=400%
2. 5340-2100=3240 пар.
Позначимо кількість дитячого взуття через Х, тоді жіночого 5Х, разом їх 6Х пар.
Складаємо рівняння
6•Х=3240;
Х=3240/6=540 пар.
Відповідь: 1) 400; 2) 540.
Далі залишилося розібрати відповіді до складніших завдань ЗНО тестів, що вимагають більших пояснень та письмової відповіді.
Якщо матеріал був Вам корисним прохання поширити його в соцмережах з метою допомоги друзям в підготовці!


