Дискретна випадкова величина Х має закон розподілу Пуассона, якщо ймовірності її можливих значень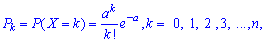
обчислюється за формулою Пуассона, де a=np<10. Як правило, Пуассонівський розподіл стосується ймовірності появи сприятливої події в великій кількості експериментів, якщо в одному – ймовірність успішного завершення прямує до нуля.
У табличній формі цей закон розподілу має вигляд
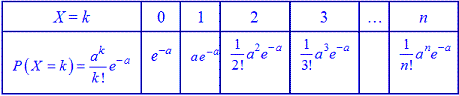Умова нормування для пуасонівського закону розподілу запишеться наступним чином
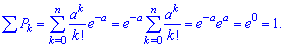Побудуємо ймовірну твірну функцію для наведеного закону:
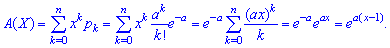Вона приймає досить простий компактний вигляд
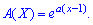Скориставшись залежностями для визначення математичного сподівання М (Х) та дисперсії D (X) через похідні від твірної функції в одиниці, дістанемо їх прості залежності
1. Математичне сподівання визначають за формулою
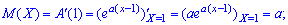
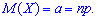
2. Маючи другу похідну від твірної функції в одиниці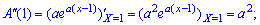
знаходять дисперсію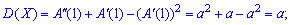
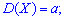Середнє квадратичне відхилення встановлюємо через квадратний корінь з дисперсії
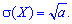Отже, для пуассонівського закону розподілу ймовірностей математичне сподівання і дисперсія рівні добутку кількості дослідів на ймовірність сприятливої події
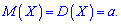На практиці, якщо математичне сподівання і дисперсія близькі за значенням то приймають гіпотезу, що досліджувана величина має закон розподілу Пуассона.
3. Асиметрія і ексцес для пуасонівського закону також рівні і обчислюються за формулами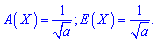
Задачі на Пуассонівський закон
Задача 1. Мікропроцесор має 10000 транзисторів, які працюють незалежно один від одного. Імовірність того, що транзистор вийде із ладу під час роботи приладу, є величиною малоймовірною і становить 0,0007. Визначити математичне сподівання М (Х) і середнє квадратичне відхилення S (Х) випадкової величини Х — числа транзисторів, що вийдуть із ладу під час роботи мікропроцесора.
Розв'язання. Задача задовільняє усім законам пуасонівського розподілу:
кількість випробувань n=10000 велика;
імовірність р=0,0007 близька до нуля;
їх добуток a=np=7<10.
На основі даних обчислюємо:
математичне сподівання M(X)
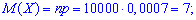
дисперсію
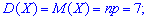
та середнє квадратичне відхилення
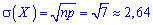
На контрольній чи тестах повтори обчислення не сладно, головне мати під рукою потрібні формули.
Задача 2. У рибальському містечку 99,99% чоловіків хоча б раз в житті були на рибалці. Проводять соціологічні дослідження серед 10000 навмання вибраних чоловіків. Визначити дисперсію D (X) і середнє квадратичне відхилення S (Х) випадкової величини Х — числа чоловіків, які жодного разу не були на рибалці.
Розв'язання. Легко переконатися, що величина Х має пуассонівський закон розподілу. Із умови задачі знаходимо
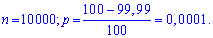
За формулами знаходимо дисперсію і середнє квадратичне відхилення
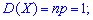
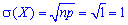
Можна знайти в гуглі ще багато подібних задач, всіх їх об'єднує зміна випадкової величини згідно закону Пуассона. Алгоритм знаходження числових характеристик наведений вище і є спільним для всіх задач, крім того формули для обчислень характеристик розподілу є достатньо простими навіть для школярів.
