Геометричний закон розподілу має місце в таких науках як мікробіологія, генетика, фізика. На практиці експеримент чи дослід здійснюють до першої появи успішної події А. Число проведених спроб буде цілочисловою випадковою величиною 1,2,.... Ймовірність появи події А в кожному досліді не залежить від попередніх і становить p, q=1-p. Ймовірності можливих значень випадкової величини Х визначається залежністю
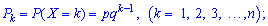
Тобто в усіх попередніх дослідах крім k-го експернимент дав поганий результат і лише в k-му був успішним. Дану формулу ймовірностей називають геометричним законом розподілу, оскільки права його частина співпадає з виразом загального елемента геометричної прогресію.
У табличній формі геометричний закон розподілу такий:
При перевірці умови нормування використовується формула суми нескінченної геометричної прогресії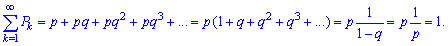
Ймовірнісну твірну функцію виражаємо за формулою
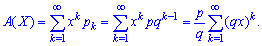Оскільки 
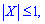то твірну функцію можна просумувати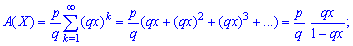
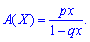
Числові характеристики для геометричного закону розподілу ймовірностей визначають за формулами:
1. Математичне сподівання обчислюємо за формулою
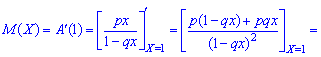
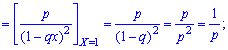
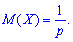
2. Дисперсію та середнє квадратичне відхилення з наступних заложнестей
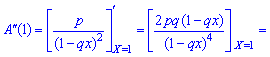
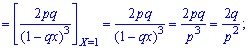
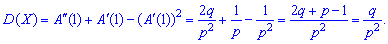
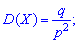
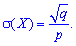
3. Коефіцієнт асиметрії та ексцес для геометричного розподілу визначають за формулою
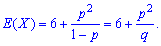
Серед дискретних випадкових величин лише геометричному закону притаманна властивість відсутності післядії. Це означає, що ймовірність появи випадкової події в k-му експерименті не залежить від того, скільки їх з'явилося до k-го, і завжди дорівнює p.
Приклад 1. Гральний кубик підкидається до першої появи цифри 1. Визначити усі числові характеристики М (Х), D (X), S (Х), A(X), E(X) для випадкової величини Х числа здійснюваних підкидань.
Розв'язання. За умовою задачі випадкова величина Х є цілочисловою з геометричним закон розподілу ймовірностей. Ймовірність успішного підкидання величина постійна і рівна одиниці розділеній на кількість граней кубика
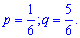
Маючи p,q необхідні числові характеристики Х знаходимо за наведеними вище формулами
математичне сподівання
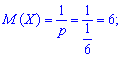
дисперсію
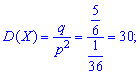
середнє квадратичне відхилення
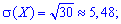
асиметрію
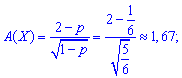
та ексцес
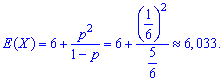
Якби всі формули ймовірності були б на стільки легкі, то можна було б її повністю перенести в шкільну програму. Однак поки що це нереально реалізвати.
Приклад 2. Мисливець-любитель стріляє з рушниці по нерухомій мішені. Імовірність влучити в мішень при одному пострілі є величиною сталою і дорівнює 0,65. Стрільба по мішені ведеться до першого влучення.
Визначити числові характеристики М (Х), D (X), S (Х), A(X), E(X) випадкової величини Х — числа витрачених мисливцем набоїв.
Розв'язання. Випадкова величина Х підпорядковується геометричниму закону розподілу тому ймовірність влучання в кожній спробі є сталою і становить p=0,65;q=1-p=0,35.
За формулами ймовірності обчислюємо математичне сподівання
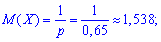
дисперсію
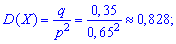
середнє квадратичне відхилення
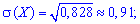
асиметрію
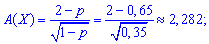
ексцес
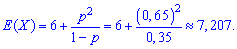
Обчислення числових характеристик для геометричного закону розподілу під силу кожному, тому користуйтеся наведеними формулами в подібних задачах і отримуйте лише правильні результати.
