На перший погляд Вам незрозуміло чому твірні функції стоять в основі розділу про закони розподілу, але це має логічне і досить просте пояснення. Вам відомо, що серед дискретних випадкових величин важливе значення в теорії ймовірностей займають такі, що набувають лише цілих невід'ємних значень Х=0,1,2,3, ... , інакше кажучи – цілочислові випадкові величини.
Для дослідження законів розподілу цілочислових випадкових величин використовують імовірнісну твірну функцію. Імовірнісною твірною функцією називають наступний збіжний степеневий ряд:
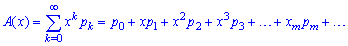
Тут pk=P(X=k) – ймовірність того, що випадкова величина Х набуде цілих значень k=0, 1, 2, 3, … .
Саме тому розділ починається з твірних функцій. Дочитавши всі статті розділу до кінця Вам стане зрозуміло, чому в усіх законах розподілу присутня імовірнісна твірна функція.
ВЛАСТИВОСТІ ІМОВІРНІСНОЇ ТВІРНОЇ ФУНКЦІЇ
1. Твірна функція А(Х) визначена в кожній точці інтервалу [–1; 1].
2. При Х=1 виконується справедливість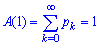
Співвідношення є умовою нормування для дискретної випадкової величини.
3. Із залежності для твірної функції А(Х) визначають ймовірність P(k)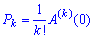
де 
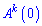— k-та похідна від твірної фнкції А(х) при Х = 0.
Отже, знаючи аналітичний вираз для А(х), завжди можна визначити ймовірність будь-якого можливого значення Х=k.
4. Похідна від твірної функції визначається співвідношенням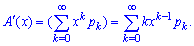
При х = 1 похідна рівна математичному сподіванню
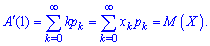Звідси отримаємо
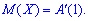5. Визначимо другу похідну твірної функції
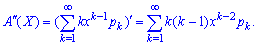При х = 1 друга похідна приймає значення
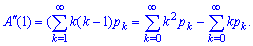Отриманий вираз можна переписати в зручній формі:
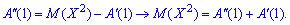На основі цього, дисперсію через похідні першого та другого порядків твірної функції
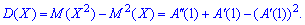можна переписати в спрощеній формі
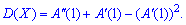ЇЇ часто використовують на практиці, при обчисленні дисперсії коли задана імовірнісна твірна функція або можна її визначити. Розглянемо варіант, коли маємо безліч несумісних подій, які виконуються при незалежних випробуваннях з ймовірністю p1,p2,...,pn. Тоді твірна функція визначається із співвідношення
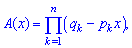де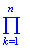 
– знак добутку, qk – ймовірність несприятливої події, яка визначається за правилом
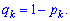Розглянемо приклади застосування твірної функції.
Приклад 1. Чотири лісовози незалежно один перевозять ліс до лісопилки. Ймовірність поламки в дорозі кожної з машин становить 0,9 для першої; для другої – 0,85; для третьої – 0,8 і 0,75 для останньої. Яка ймовірність того, що без поломок доїде три лісовози з чотирьох? Яка ймовірність, що не більше двох лісовозів доїдуть справними до лісопилки?
Розв'язання. Імовірності кожної з подій різні та утворюють незалежні випробування. Для відшукання відповіді на обидва запитання побудуємо твірну функцію.
Для неї вхідні дані приймуть заначення
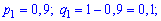
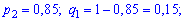
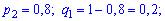
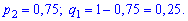
Підставимо знайдені величини в твірну функцію
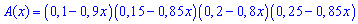
та розкладемо в ряд за степенями змінної. В результаті отримаємо поліном
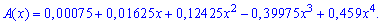
За властивостями твірної функції коефіцієнти при степенях аргументів є ймовірностями виконання події (довезення лісу без поломки) рівно стільки раз – який степінь аргумента.
На основі цього, ймовірність події Р(А), що доїде три лісовози без поломки входить в твірну функцію при x3 і становить
Р(А)=0,39975.
Ймовірність події Р(B) можна росписати як суму ймовірностей, що доїде один лісовоз + доїде два лісовози+не доїде жодного.
Відповіді названим доданкам ймовірності шукаємо при відповідних їм степенях твірної функції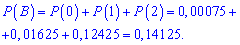
Як бачите обчислення не складні, головне зрозуміти суть завдання. Також можете переконатися, що виконується умова нормування
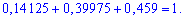
Якщо трапиться, що при обчисленнях у Вас не виконується умова нормування, тоді потрібно шукати помилку при розкладі твірної функції в ряд за степенями х і виправити її.
