Перш ніж перейти до готових відповідей на задачі з комбінаторики уважно перегляньте схему, яка показує коли використовувати розміщення, перестановки, комбінації. Саме від відповіді на питання:
чи повторюються елементи у вибірці?
чи важливий порядок розміщення елементів? та
чи всі елементи входять у вибірку?
залежить вибір формули, а отже і правильність обчислень.
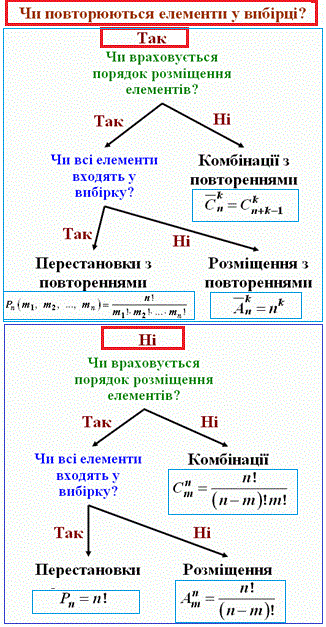
Роздрукуйте наведені комбінаторні формули і використовуйте як шпаргалку. Їх завжди можна знайти онлайн, але краще мати під рукою при розв'язуванні наступних завдань. Також вивчайте властивості факторіалів, адже їх постійно доведеться спрощувати.
Задачі з комбінаторики
Приклад 1. Скількома способами можна сформувати потяг з 7 вагонів?
Обчислення: Беремо до уваги, що вагони різні, тому будь-яка перестановка вагонів це інший потяг.
Крім того в формуванні вагонів бере участь вся їх кількість, тому тут використовуємо формулу перестановок P7 :
n=P7=7!=7*6*5*4*3*2*1=5040.
Приклад 2. Скількома способами можна розподілити три різні путівки між 10 працівниками?
Обчислення: Першу путівку можна дати одному з 10 працівників, після чого залишиться 2 путівки і 9 працівників, і останню путівку можна розподілити серед 8 працівників. На мові ймовірностей – це розміщення з 10 по 3:
n=A103=10!/(10-3)!=10*9*8=720.
Приклад 3.В олімпіаді бере участь 7 команд. Скількома способами між ними можна розподілити золоту, срібну та бронзову медалі:
а) якщо одна команда може взяти лише одну медаль?
б) якщо усі команди можуть вибороти кожну з медалей
Обчислення: а) Першу медаль отримає 1 з 7 команд, другу 1 з 6, третю 1 з 5, тому:
m1=A73=7!/(7-3)!=7*6*5=210.
б) За правилом добутку на кожну медаль претендує 7 команд, тому кількість способів рівна 7^3:
m2=7*7*7=343.
Відповідь: 210, 343.
Приклад 4. На столі є 7 ручки та 3 олівці. Скількома способами можна взяти зі столу один предмет?
Обчислення: Взяти один предмет означає або олівець, або ручку. На мові ймовірності всюди "або" замінюємо додаванням.
1 ручку з 4 можна вибрати 4 способами,
1з 3 олівців вибирають 3 способами.
Сумарно
n=7+3=10.
Відповідь: 10.
Приклад 5. Скільки різних п'ятицифрових чисел можна скласти з цифр 2, 3, 4, 5, 6, 7, 8?
Обчислення: Не всі цифри з вибірки (7 цифр) входять у п'ятицифрове число + цифри не повторюються і порядок має значення, тому використовуємо формулу розміщень без повторень
n=A75=7!\2!=2520.
Відповідь: 2520.
Приклад 6. Скільки різних тризначних чисел можна скласти з цифр 0, 1, 2, 3, 4, 5?
Обчислення: Подібні приклади є винятком з правил, тому що "0" на перше місце поставити не можемо. Залишається 5 цифр з 6, тоді за першою не рівною нулю йдуть розміщення з 5 інших цифр по 2:
n=5*A52=5*5!/3!=100.
Відповідь: 100.
Приклад 7. У кошику 6 мандаринів та 8 апельсинів. Остап вибирає або мандарин, або апельсин. Після цього Софія вибирає з фруктів, що залишилися, мандарин й апельсин одночасно. Скільки можливостей такого вибору?
Обчислення: Від вибору Остапа залежить з якого набору буде вибирати Софія. Якщо Остап вибере мандаринку 1 з 6 способами, то Софії буде мати вибір з 6-1=5 мандарин і 8 апельсин (5*8), в іншому разі вона зможе обрати з 6 мандарин і 7 апельсин (6*7). Або такий або такий набір означає, що потрібно застосувати правило суми ймовірностей.
n=6*5*8+8*6*7=240+336=576.
Відповідь: 576.
Приклад 8. У маленької Юлі є багато синіх, червоних, жовтих та зелених кубиків.
(а) Скільки різних веж висотою в 6 кубиків може побудувати Юля?
(б) Скільки серед цих веж містять хоча б один синій кубик?
(в) Скільки серед цих веж містять хоча б один синій або зелений кубик?
Обчислення: Тут потрібно буде використати протилежну подію до двох останніх пунктів задачі.
а) Кожен ряд вежі можна викласти з синього, червоного, жовтого та зеленого кубика. Тобто одного з чотирьох кольорів, тому різних веж може бути
n=4^6=4096.
б) Хоча б один синій кубик означає, або один або два ... або 6. Це передбачає багато обчислень, простіше від всеможливої кількості веж відняти протилежну подію - не містить жодного синього кубика. А це означає, що вежі формуються з 3 кольорів - зелений,жовтий, червоний.
Тому їх кількість рівна
m=n-3^6=4096-729=3367.
в) Логічно, що веж, що містять хоча б один синій або зелений кубик має бути більше ніж тих, що містять хоча б один синій. Але як це врахувати?
І знову приходить на допомогу теорема про протилежну подію, від всіх знайдених віднімемо ті, що не містять ні синього ні зеленого кубика.
Думаю, що тепер Ви здогадалися подальші обчислення. Від n=4096 віднімемо всі, що складаються лише з червоного та жовтого кубика, а їх буде 2^6:
m2=n-2^6=4096-64=4032.
Відповідь: 4096, 3367, 4032.
Приклад 9. Скількома способами можна вибрати 2 білі і 1 рожеву троянду з 10 білих і 5 рожевих троянд?
Обчислення: Завдання на множення ймовірностей. Оскільки порядок входження троянд в букет не важливий, то потрібно застосувати формулу комбінацій, а не розміщень, тому кількість способів вибрати 2 білі з 10 рівна C102:
m1=C102=10!/(8!*2!)=45.
Тоді одну рожеву з 5 можна вибрати 5 способами m2=5.
Загальна кількість вибрати 1 рожеву та 2 білі троянду за формулою множення ймовірностей рівна
n=m1*m2=45*5=225.
Відповідь: 225.
Приклад 10. Скількома способами можна вибрати чотирьох чергових із класу, у якому 15 учнів?
Обчислення: Тут нам неважливий порядок входження, а лише потрібно знайти кількість різних груп по 4 чергових з 15. Тому кількість способів рівна комбінації з 15 по 4:
n=C154=15!/(11!*4!)=15*14*13*12/(4*3*2*1)=1365.
Приклад 11. Скількома способами можна розділити 6 різних цукерок між трьома дітьми, якщо кожна дитина отримує по дві цукерки?
Обчислення: Перше, що ви маєте зауважити це те, що цукерки різні, тому вже слід застосовувати комбінації (сполучення).
Другий момент – це як розподілити, якщо порівно, то всі матимуть по 6:3=2 цукерки, якщо ні – то кількість способів росте.
Підемо простим шляхом, поділимо порівну, тоді перша дитина отримає 2 з 6 цукерок, друга – 2 з 4, третя 2 з 2.
За теоремою множення
n=C62*C42*C22=6!/(4!*2!)*(4!/(2!*2!))*1=15*6*1=90.
Відповідь: 90.
Приклад 12.Скільки різних "слів" можна отримати, переставляючи букви в слові "Математика"?
Обчислення: Оскільки слово "Математика" має букви, що повторяються, то використовуємо перестановки з повтореннями.
Всього "Математика" має 10 букв, дві букви "м" і три "а".
Тому кількість перестановок рівна
n=P10(2,3)=10!/(2!*3!)=302400.
Відповідь: 302400.
Приклад 13.Скільки різних "слів", у яких комбінація букв "бук" йде разом можна отримати, переставляючи букви в слові "букварик"?
Обчислення: Нові "слова" повинні містити "бук" як одну букву, тому переміщати будемо
"бук" "в" "а" "р" "и" "к", тобто 6 "букв".
Для знаходження кількості слів використовуємо формулу перестановок
n=P6=6!=720.
Відповідь: 720.
Приклад 14. В колоді 36 карт, з них 4 тузи. Скількома способами можна вибрати 5 карт так, щоб серед них було 3 тузи?
Обчислення: Порядок входження нас не цікавить, головне набір в якому 3 тузи і 2 інші карти.
3 тузи з 4 можна вибрати C43 способами, лишається 36-4=32 карти, з яких 2 вибираємо C322 способами.
За правилом множення ймовірностей дістанемо:
n=C43*C322=4*(32*31/2)=1984.
Приклад 15. З колоди з 52 карти навмання взяли 4 карт. В скількох випадках буде хоча б одна шістка?
Обчислення:Обчислимо виходячи з протилежної події.
Кількість різних наборів з 52 карт по 4 рівна C524, але серед них є ті, що не містять шістки. Тому від знайденої кількості віднімемо випадки коли серед 4 карт немає 6. Це можливо, коли вибираємо 4 з 52-4=48 (віднімаємо чотири 6 з колоди).
Таких наборів буде C484.
Остаточно отримаємо:
n=C524-C484=52*53*51*50/(4*3*2)-48*47*46*45/(4*3*2)=292825-194580=98245.
Ось така непроста комбінаторика!
Тут головне знати комбінації чи перестановки використовувати, та чи важливі повторення, все решта зводиться до вибору формули та вміння спрощувати факторіали.
Уважно перегляньте алгоритми обчислень, оскільки на їх основі побудовані складніші задачі з ймовірності, які чекають Вас на практичних, розрахункових, тестах. Цікаві комбінаторні завдання поступово будуть оформлені в нові уроки, оскільки в 15 прикладах всіх нюансів важко пояснити.


