Продовжуємо серію статей на тему спрощення тригонометричних виразів і сьогодні переглянемо чергові відповіді до завдань із ЗНО підготовки. Приклади підібрані так, що з ростом їх номера росте і складність обчислень. Тому, якщо Вам наступні приклади є важкими в плані сприйняття, то можете почати з перегляду попередніх 10 відповідей, де добре описані формули перетворення синусів, косинусів, тангенса та котангенса.
Завдання 7.16 Обчислити суму косинусів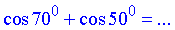
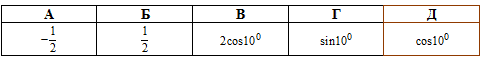
Розв'язування: Потрібно знайти суму косинуса 70 та 50 градусів.
Кінцевого значення у вигляді чмсла ми не отримаємо, а лише спростимо вираз до одного із варіантів заданих у тестових відповідях із ЗНО.
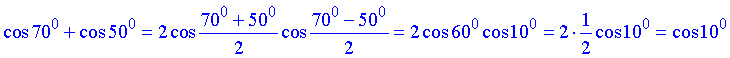
Тут використали формулу переходу від суми косинусів кутів до добутку косинусів півсуми та піврізниці кутів:
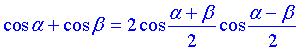
Відповідь: Д.
Завдання 7.17 Знайти значення виразу 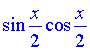 , якщо аргумент приймає значення
, якщо аргумент приймає значення 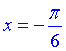 .
.
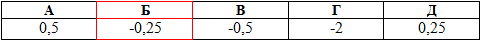
Розв'язування: Для спрощення виразу зведемо його під формулу синуса подвійного кута:
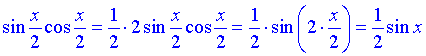
Далі підставляємо заданий кут та обчислюємо
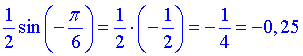
Відповідь: Б.
Завдання 7.18 Обчислити добуток косинусів 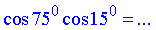

Розв'язування: Добуток косинусів 75 та 15 перетворимо до суми косинусів суми та різниці цих кутів
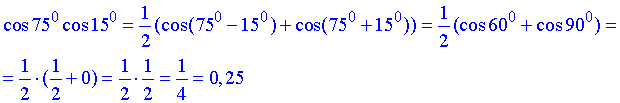
Кінцеві кути приймають 60 та 90 градусів, тому їх косинуси відомі та спрощують обчислення
Відповідь: Г.
Завдання 7.19 Визначити значення виразу 
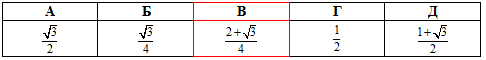
Розв'язування: Знайдемо добуток синуса 105 градусів на косинус 15 градусів.
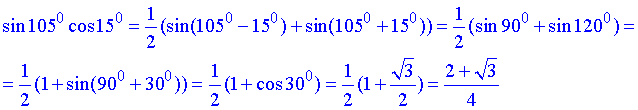
Тут використали формули представлення добутку кутів через суму синусів
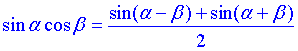 і
і 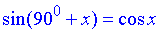
Відповідь: В.
Завдання 7.20 Знайти добуток синусів 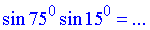
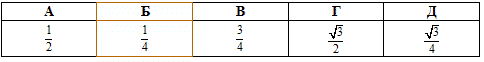
Розв'язування: Обчислимо добуток синусів 75 та 15 градусів, записавши добуток синусів через різницю косинусів
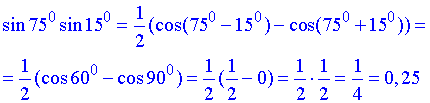
Відповідь: Б.
Завдання 7.21 Обчислити синус арккосинуса 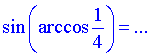
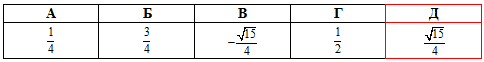
Розв'язування: Щоб обчислити синус від арккосинуса застосуємо відому тригонометричну тотожність
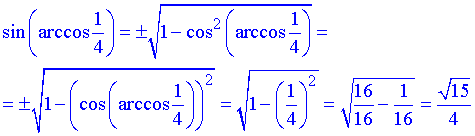
Кут 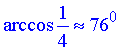 знаходиться у І чверті, тому синус від арккосинуса додатний
знаходиться у І чверті, тому синус від арккосинуса додатний
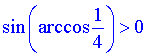
Відповідь: Д.
Завдання 7.22 Обчислити косинус подвоєного арксинуса 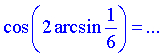
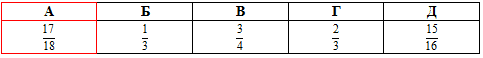
Розв'язування: Знайдемо косинус від подвійного арксинуса через формулу косинуса подвійного кута
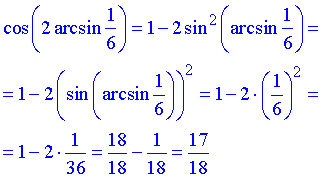
Тут використали формулу косинуса подвійного кута
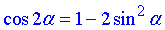
Відповідь: А.
Завдання 7.23 Обчислити тангенс половини арксинуса 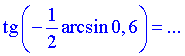
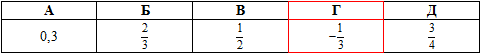
Розв'язування: Щоб знайти тангенс від заданого арксинуса скористаємося формулою тангенса половини кута
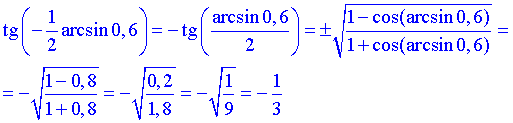
Кут 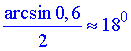 знаходиться у І чверті, тому тангенс арксинуса додатний
знаходиться у І чверті, тому тангенс арксинуса додатний 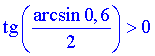
Тут мали
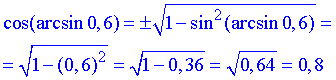
Кут 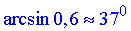 знаходиться у І чверті, тому косинус арксинуса додатний
знаходиться у І чверті, тому косинус арксинуса додатний

Відповідь: Г.
Завдання 7.24 Знайти косинус арккотангенса 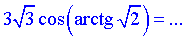
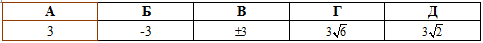
Розв'язування: Косинус від арктангенса спростимо наступним чином
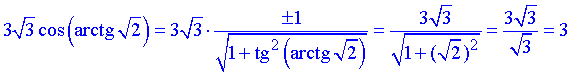
Кут 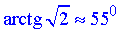 знаходиться у І чверті, тому косинус арккотангенса додатний
знаходиться у І чверті, тому косинус арккотангенса додатний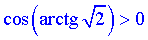
Тут використали наступну формулу косинуса кута через тангенс
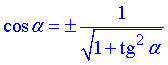
Відповідь: А.
Завдання 7.25 Знайти значення виразу 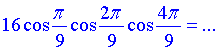
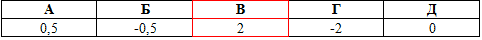
Розв'язування: Маємо добуток трьох косинусів. При первинному аналізі важко сказати як спрощувати такий вираз, але схема відома і давно вже розжована.
Спершу потрібно перейти до синуса подвійного кута, а для цього домножаємо та ділимо на синус першого кута
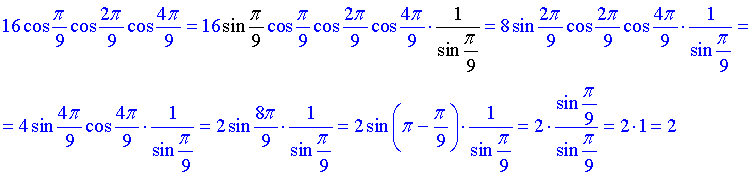
І так кілька разів. Тут важливо не забувати слідкувати за множником (1/2), який фігурує в формулі синуса подвійного кута.
Такий штучний прийом часто застосовується в тригонометрії і з наступних прикладів Ви в цьому переконаєтеся.
Відповідь: В.
Завдання 7.26 Обчислити 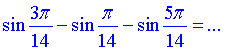
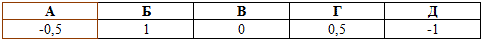
Розв'язування: Потрібно знайти різницю трьох синусів. Для цього використаємо наступний прийом:
домножимо та поділимо на косинус найменшого кута. В цьому випаду в дужках отримаємо синус подвійного кута та інші вирази, які після нескладних перетворень скоротяться та дадуть у відповіть ціле значення -0,5.
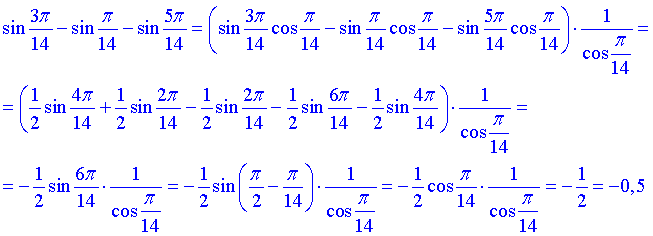
Відповідь: А.
Завдання 7.2а Спростити вираз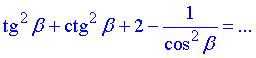
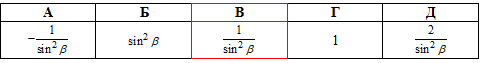
Розв'язування: Для спрощення виразу розпишемо суму квадратів тангенса та котангенса через частки синусів та косинусів.
Далі використаємо відомі тригонометричні тотожності та зведемо вираз до однієї з тестових відповідей із ЗНО.
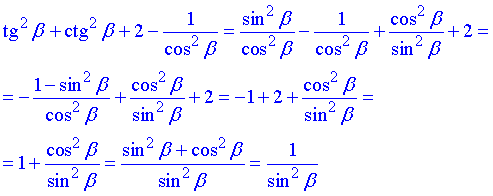
Відповідь: В.
Завдання 7.4 а Обчислити 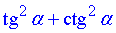 , якщо відома сума тангенса та котангенса
, якщо відома сума тангенса та котангенса  .
.
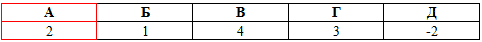
Розв'язування: Потрібно знайти суму квадратів тангенса та котангенса.
Для цього піднесемо до квадрату суму тагенса та котангенса та спростимо отриманий вираз
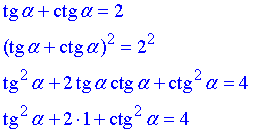
звідси отримаємо
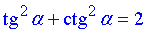
Тут використали тотожніть
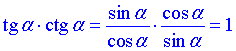
Відповідь: А.
Завдання 7.5а Обчислити 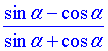 , якщо відомий тангенс кута
, якщо відомий тангенс кута 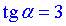 .
.

Розв'язування: Щоб отримати тангенс поділимо і чисельник і знаменник дробу на косинус кута.
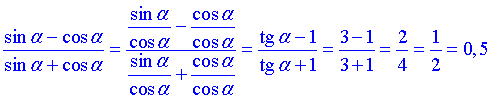
В такий спосіб частка косинусів дасть одиницю + дістанемо тангенси, які відомі за умовою завдання.
Отримаємо варіант В тестів ЗНО.
Відповідь: В.
Всі наступні завдання містять чотири підпункти і потрібно встановити відповідність між правою та лівою частиною співвідношень.
Завдання 7.27 Установити відповідність між виразами (1 - 4) та виразами, які їм тотожно дорівнюють (А - Д).
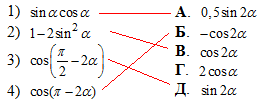
Розв'язування: Завдання на знання тригонометричних формул.
Раніше аналогічні приклади зустрічалися, тому без проблем приходимо до наступних відповідей
1)  А,
А,
2) 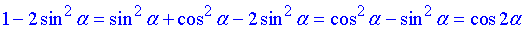 В,
В,
3) 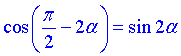 Д,
Д,
4) 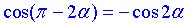 Б.
Б.
Завдання 7.28 Установити відповідність між виразами (1 - 4) та виразами, які їм тотожно дорівнюють (А - Д).
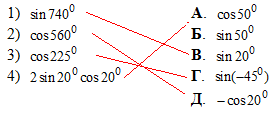
Розв'язування: Щоб знайти відповіді на перші три завдання із ЗНО тестів необхідно врахувати, що період синуса та косинуса рівний 360 градусів, а також їх парність чи непарність при переході 0.
1) 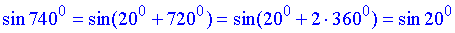 В,
В,
2)  Д,
Д,
тут використали періодичність функцій:
 і
і  , де k - ціле число.
, де k - ціле число.
3) 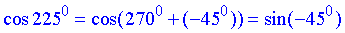 Г,
Г,
тут використали формулу зведення: 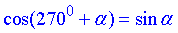
4) 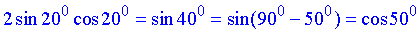 А.
А.
Завдання 7.29 Установити відповідність між виразами (1 - 4) та виразами, які їм тотожно дорівнюють (А - Д).
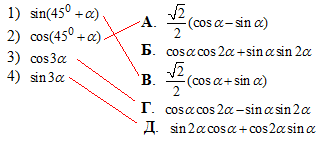
Розв'язування: В перших двох прикладах синус суми та косинус суми розписуємо через суму та різницю добутків синусів та косинусів, а далі підставляємо кути
1) 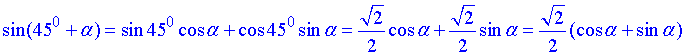 В,
В,
2) 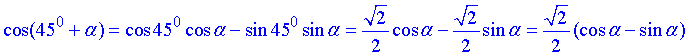 А,
А,
Третій та четвертий приклад розписуємо, розписавши потрійний кут як сума "альфа +2альфа"
3) 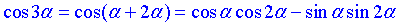 Г,
Г,
4) 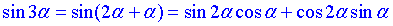 Д.
Д.
Завдання 7.30 Одна зі сторін кута збігається з додатною піввіссю абсцис, а інша перетинає одиничне коло в точці
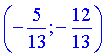 .
.
Установити відповідність між тригонометричними функціями кута 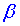 (1 - 4) та їх значеннями (А - Д).
(1 - 4) та їх значеннями (А - Д).
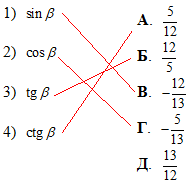
Розв'язування: Спершу для повного уявлення, що нам задано, відкладемо один з відрізків на осі і знайдемо точку перетину з одиничним колом, щоб при цьому зберігався знак другого відрізка. В результаті отримаємо наступний кут
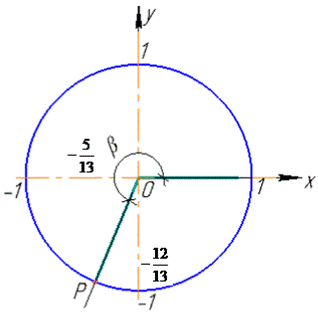
Враховуючи завдання 7.2 і формули у завданнях 7.4, 7.5, отримаємо
1) 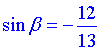 В,
В,
2) 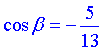 Г,
Г,
3) 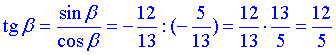 Б,
Б,
4) 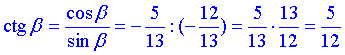 А.
А.
В наступній статті розглянемо останні 20 прикладів із ЗНО підготовки на спрощення тригонометричних виразів.


