Нерівності, що містять sin(x), cos(x), tg(x), ctg(x) з однієї сторони від знаку нерівностей (<,≤,>,≥) називають найпростішими тригонометричними нерівностями. Приклади найпростіших тригонометричних нерівностей мають вигляд:
sin(x)≤√2/2, cos(x)>-1/2, tg(x)<1, ctg(x)≥√3 і тому подібних.
Якщо маємо знаки < або > то нерівність називається строгою, якщо ≤ або ≥ то нерівність є нестрогою.
Розв'язати тригонометричну нерівність означає знайти множину значень аргументу "ікса", включаючи періодичність функцій, при яких виконується нерівність.
Важливо, щоб в синусах та косинусах права сторона за знаком нерівності не перевищувала за модулем одиниці. Інакше виходимо за межі ОДЗ цих функцій і такі нерівності не мають коренів. Тому спершу перевіряємо область допустимих значень, а далі розв'язуємо нерівність. Тангенс та котангенс не потрібно перевіряти на ОДЗ оскільки вони приймають як завгодно як великі, так і малі значення. Однак, вони мають розриви в точках вертикальних асимптот, що призводить до скорочення інтервалу розв'язків.
Під складними тригонометричними нерівностями мають на увазі такі, де аргумент міститься під модулем, коренем квадратним, з множником або ж маємо комбінацію тригонометричних функцій чи над нею виконуються певні дії (модуль, квадрат, корінь і т.д.)
ЗНО підготовка. Найпростіші тригонометричні нерівності
Завдання 19.1 Розв'язати нерівність sin(x)<√2/2.
Розв'язання: Спершу перевіряємо праву частину нерівності на входження в ОДЗ синуса. Для косинуса таку перевірку теж робіть.
Здебільшого викладачі вимагають виконувати перевірку на ОДЗ функцій.
Оскільки умова виконується|√2/2|≤1, то розв'язок нерівності для синуса існує.
Далі є два методи розкриття нерівності:
Графічно з побудовою заданих функцій (їх не важко будувати) і з використанням одиничного кола.
Другий спосіб більш поширений на практиці, оскільки будувати одиничне коло і наносити на нього прямі куди простіше ніж повні графіки функцій.
Однак і про перший метод Ви повинні знати, та вміти знаходити розв'язки тригонометричних нерівностей.
І спосіб:
Побудуємо в одній системі координат графіки функцій y=sin(x) і y=√2/2 та виділимо проміжки, на яких графік функції y=sin(x) розташований нижче від графіка прямої y=√2/2.
Нижче, оскільки заданий знак нерівності строго менше.
Якщо нерівність нестрога, то точки перетину включаємо в розв'язок і дістаємо проміжок.
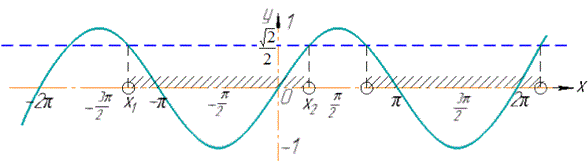
Знайдемо абсциси точок x1 і x2 (x1< x2) - перетину графіків зазначених функцій:
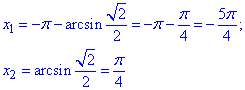
Запишемо відповідь, врахувавши період функції y=sin(x).
Отже, розв'язком нерівності є множина значень
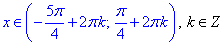
ІІ спосіб:
Побудуємо одиничне коло, пряму y=√2/2 і позначимо точки Px1 і Px2 перетину одиничного кола й зазначеної прямої та виділимо множину точок, ординати яких менші √2/2.
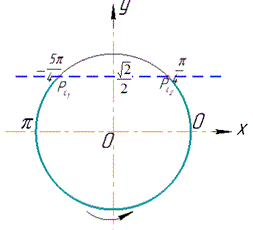
x1 і x2, здійснюючи обхід дуги проти годинникової стрілки:
x1<x2,
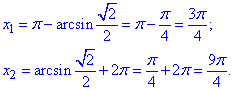
Отже,
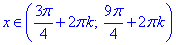
або

2Пі є періодом для синуса y=sin(x), тому при додаванні або відніманні на це число множина розв'язків нерівності не зміниться)!
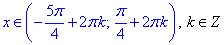
Завдання 19.2 Розв'язати нерівність cos(x)>√3/2
Розв'язання: Оскільки |√3/2|≤1, то розв'язок нерівності існує.
І спосіб:
Побудуємо в декартовій системі координат графіки функцій y=cos(x) і y=√3/2 та виділимо проміжки, на яких графік функції y=cos(x) розташований вище прямої y=√3/2.
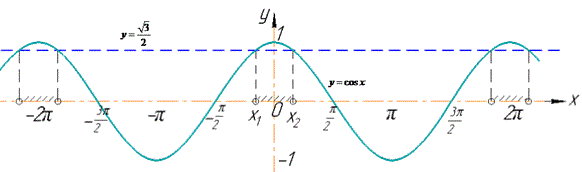
Знайдемо абсциси точок x1 і x2 (x1<x2) - перетину графіків зазначених функцій через арккосинус:
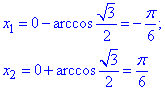
Добавляємо період косинуса 2Пі та записуємо множину розв'язків нерівності:
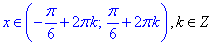
ІІ спосіб:
Побудуємо одиничне коло, пряму х=√3/2 і позначимо точки Px1 і Px2 перетину одиничного кола й зазначеної прямої та виділимо множину точок, ординати яких більші √3/2.
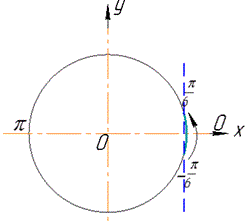
Знайдемо значення кутів x1 і x2, здійснюючи обхід дуги проти годинникової стрілки:
x1<x2,
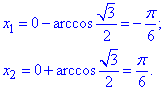
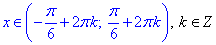
Уважно пергляньте ці два приклади та запам'ятайте, що для синуса пряму будуємо паралельно "іксу", а для косинуса паралельно "ігрику".
Це пов'язано з самим означенням синуса та косинуса на одичному колу.
Завдання 19.3 Розв'язати нерівність tg(x)<√3.
Розв'язання:
І метод:
Побудуємо в декатовій СК функції y=tg(x) та y=√3.
Наступним кроком виділяємо проміжки, на яких графік функції y=tg(x) розташований нижче від графіка прямої y=√3.
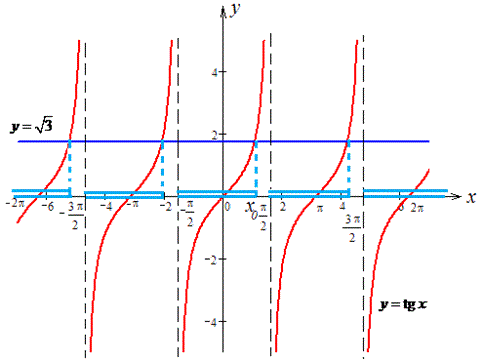
Не забувайте, що тангенс має розриви і в точках розриву (в асимптотах) множина розв'язків обривається.
Знайдемо через арктангенс абсцису точки x0 - перетину графіків зазначених функцій, яка є кінцем одного з проміжків, на якому виконується задана нерівність x0=arctg(√3)=Pi/3.
Іншим кінцем цього проміжку є точка –Pi/2, у якій функція y=tg(x) невизначена (розрив ІІ роду).
Таким чином, одним із проміжків розв'язку заданої нерівності є –Pi/2<x<Pi/3.
Враховуючи, що період тангенса рівний Пі записуємо залальний розв'язок нерівності
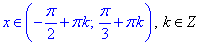
ІІ метод:
Побудуємо одиничне коло, лінію тангенсів, на якій позначимо точку Tx(1;√3) і виділимо ту частину лінії тангенсів, яка розміщена нижче точки Tx та дугу кола, яка відповідає виділеній частині лінії тангенсів.
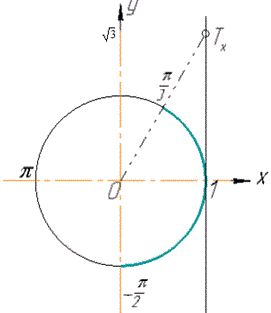
Запишемо значення кутів, які відповідають виділеній дузі:
-Pi/2<x<arctg(√3), або –Pi/2<x<Pi/3.
Запишемо відповідь, врахувавши періодичність y=tg(x).
Отримали наступну множину розв'язків нерівності:
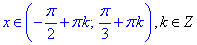
Завдання 19.4 Розв'язати нерівність ctg(x) ≤-√3/3.
Розв'язання:
І метод:
Побудуємо в декартовій СК графіки y=ctg(x) і y=-√3/3 та виділимо інтервали, на яких графік функції y=ctg(x) розташований не вище від графіка прямої y=-√3/3.
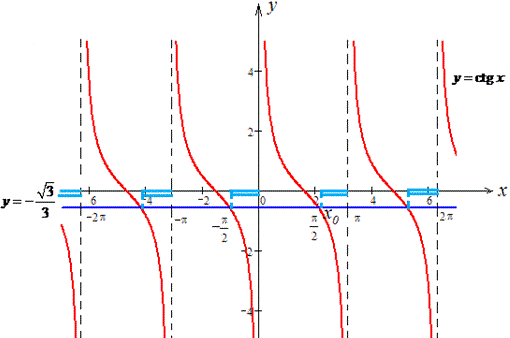
Наступним кроком знаходимо абсцису точки x0 - перетину графіків зазначених функцій.
Шукана точка є кінцем одного з проміжків, на якому виконується задана нерівність
x0=arctg(-√3/3)=2Pi/3
(якщо точно: arctg(-√3/3)=-Pi/3, але враховуючи період Pi котангенса y=ctg(x), то –Pi/3+Pi=2Pi/3).
Іншим кінцем цього проміжка є точка Pi, у якій функція y=ctg(x) має вертикальну асимптоту.
Таким чином, одним із проміжків розв'язку заданої нерівності є 2Pi/3≤x<Pi.
Добавляємо періодичність котангенса та записуємо множину розв'язків нерівності:
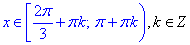
ІІ метод:
Будуємо одиничне коло з лінію котангенсів, на якій позначаємо точку Tx(-√3/3;1) і виділяємо ту частину лінії котангенсів, яка розміщена ліворуч від точки Tx та дугу кола, яка відповідає виділеній частині лінії котангенсів.
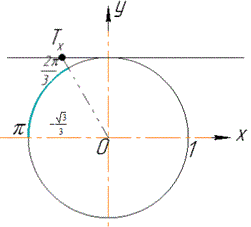
Записуємо значення кутів, які відповідають виділеній дузі:
arctg(-√3/3) ≤ x<Pi, або 2Pi/3≤x<Pi.
Запишемо відповідь, врахувавши періодичність функції y=ctg(x).
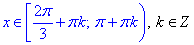
Завдання 19.5 Розв'язати нерівність sin(x)<√3/2..
Розв'язання: Виконуємо перевірку входження правої частини нерівності в ОДЗ синуса:
|√3/2|≤1, отже розв'язок нерівності існує.
Побудуємо одиничне коло, пряму y=√3/2 і позначимо дві точки Px1,Px2 перетину одиничного кола й побудованої прямої.
Виділимо дугу з точками, ординати яких менші за √3/2.
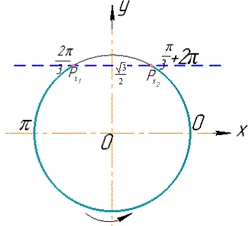
Знайдемо значення кутів x1 і x2, здійснюючи обхід дуги проти годинникової стрілки:
x1<x2,
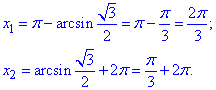
Добавлямо 2Pi·k, щоб отримати всю множину розв'язків нерівності з синусом:
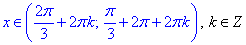
Завдання 19.6 Розв'язати нерівність cos(x)>1/2.
Розв'язання: Оскільки |1/2|≤1, то розв'язок нерівності існує.
Побудуємо одиничне коло, пряму y=1/2 і позначимо точки P[x1] і P[x2] перетину одиничного кола й зазначеної прямої та виділимо множину точок, ординати яких більші ніж 1/2.
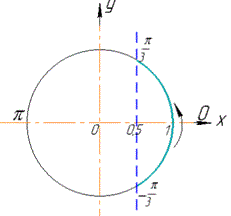
Знайдемо значення x1 і x2, здійснюючи обхід дуги проти годинникової стрілки:
x1<x2,
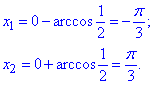
Додаємо періодичність косинуса та записуємо загальний розв'язок нерівності:
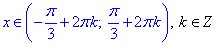
Завдання 19.7 Розв'язати нерівність tg(x)<1.
Розв'язання: Побудуємо одиничне коло, лінію тангенсів, на якій позначимо точку Tx(1;1) і виділимо ту частину лінії тангенсів, яка розміщена нижче точки Tx та дугу кола, яка відповідає виділеній частині лінії тангенсів.
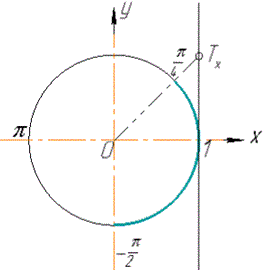
Запишемо значення кутів, які відповідають виділеній дузі:
-Pi/2<x<arctg(1), або –Pi/2<x<Pi/4.
Запишемо відповідь, врахувавши період функції y=tg(x).
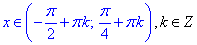
Завдання 19.8 Розв'язати нерівність ctg(x) ≥√3.
Розв'язання: Побудуємо одиничне коло, лінію котангенсів, на якій позначимо точку Tx(√3;1) і виділимо ту частину лінії котангенсів, яка розміщена праворуч від точки Tx та дугу кола, яка відповідає виділеній частині лінії котангенсів.
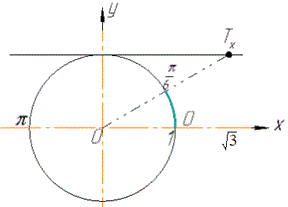
Запишемо значення кутів, які відповідають виділеній дузі:
0<x≤arctg(√3), або 0<x≤Pi/6.
Запишемо відповідь, врахувавши період функції y=ctg(x).
x∈(Pi•k;Pi/6+Pi•k], k∈Z.
Уважно перегляньте та запам'ятайте як будувати лінії синуса, косинуса, тангенса та котангенса на одиничному колі.
З цим переважно у студентів виникають труднощі, через які всі по своєму трактують визначення кутів на колі.
Другий метод є поширенішим на практичних, тож постарайтеся вивчити хоча б його.
Як тільки освоїте все, що написано вище можете сміло братися за наступну статтю в якій розберемо відповіді на складні геометричні нерівності.


