Тригонометричні приклади на визначення найменшого додатного розв'язку нічим не відрізняються від усіх завдань, що були нами розглянуті раніше. Єдина умова, що вкінці обчислень необхідно підібрати номер за якого отримаємо найменший додатний корінь тригонометричного рівняння. Обчислення ускладнюються коли маємо вложені рівняння, корені квадратні або рівняння другого порядку.
В даній статті будемо аналізувати відповіді до складніших завдань, оскільки прості розглядали вже раніше та на них Ви навряд чи чогось нового навчитеся, чи зможете підготуватися до тестування та вступу у ВУЗи.
Тригонометричні завдання із ЗНО підготовки
Приклад 18.36 Розв'язати рівняння 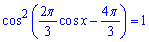
У відповідь записати найменший додатний корінь, округлений з точністю до 0,1.
Розв'язання: Маємо складне тригонометричне рівняння.
Квадрат косинуса рівний одиниці можна представити як косинус рівний плюс мінус одиниці, або косинус за модулем рівний одиниці.
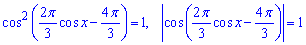
Розділимо рівняння на два випадки та розв'яжемо:
Через арккосинус позбуваємося зовнішнього косинуса
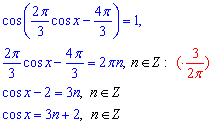
Далі за умовою існування коренів рівняння (ОДЗ) знаходимо номер
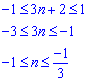
звідси n=-1.
Отже, cos(x)=-1,
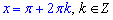
Найменший додатний корінь отримуємо при k=0 і він рівний x=Pi.
При від'ємному значенні підмодульного косинуса матимемо:
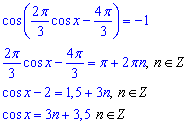
При врахуванні ОДЗ дістанемо наступну подвійну нерівність для визначення номера
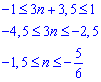
звідси n=-1.
При цьому отримаємо cos(x)=-3•(-1)+3,5=1/2,
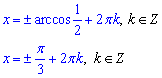
Найменший додатний кут матимемо при k=0, x=Pi/3.
Порівнюючи обидва значення приходимо до висновку, що x=Pi/3 найменший додатний корінь, або після округлення до десятих x≈1.0.
Відповідь: 1,0.
Приклад 18.40 Розв'язати рівняння 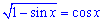 .
.
У відповідь записати значення кореня розділене на Пі (x0/Pi), де x0 - найменший додатний корінь рівняння.
Розв'язання: Спершу випишемо обмеження, які накладаються на рівняння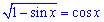 у зв'язку з присутністю в лівій частині кореня квадратного:
у зв'язку з присутністю в лівій частині кореня квадратного:
ОДЗ: 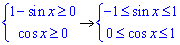
Підносимо обидві частини рівняння до квадрату, щоб позбутися кореня
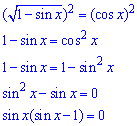
Отримане рівняння розділяємо на 2:
sin(x)=0, x=Pi•n, n∈Z.
При n=1 маємо x1=Pi - найменший додатний корінь рівняння sin(x)=0.
Друге тригонометричне рівняння неоднократно вже розглядали:
sin(x)=1, звідси
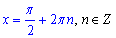
При n=0 маємо x2=Pi/2- найменший додатний корінь рівняння sin(x)=1.
Порівнюючи "ікси", робимо висновок що x0=Pi/2 - найменший додатний корінь заданого рівняння.
Виконуємо нормування на Пі
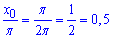 .
.
Відповідь: 0,5.
Приклад 18.42 Розв'язати рівняння cos(x)=sin(3x).
У відповідь записати значення x0/Пі, де x0 - найменший додатний корінь рівняння.
Розв'язання: Перетворимо різницю тригонометричних функцій cos(x)=sin(3x), cos(x)-sin(3x)=0 за формулою зведення до добутку
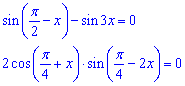
Отримане рівняння розділяємо на два та по черзі розкриваємо:
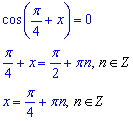
При n=0 маємо x1=Pi/4 - найменший додатний корінь рівняння 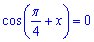 .
.
Для синуса матимемо:
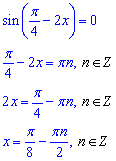
При n=0 маємо x2=Pi/8- найменший додатний корінь рівняння 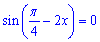 .
.
Отже, x0=Pi/8 - найменший додатний корінь заданого рівняння cos(x)=sin(3x).
Залишилося пронормувати корінь на Пі:
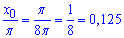
Відповідь: 0,125.
Приклад 18.43 Розв'язати рівняння 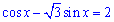 .
.
У відповідь записати значення 3x0/Пі, де x0 - найменший додатний корінь рівняння.
Розв'язання: Поділимо рівняння на двійку та, замінивши множники на синуси та косинуси одного і того ж кута, застосовуємо одну із формул зведення:
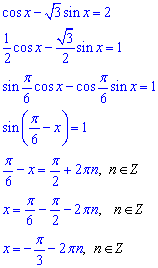
Далі функцію під синусом прирівнюємо до арксинуса одиниці та виражаємо сам аргумент.
При n=-1 маємо x0=5Pi/3- найменший додатний корінь заданого рівняння.
Множимо його на трійку та ділимо на Пі
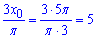
Відповідь: 5.
Приклад 18.47 Нехай x0 - найменший додатний корінь рівняння
cos2(x)-5sin(x)•cos(x)+2=0.
Знайти tg(x0).
Розв'язання: Перетворимо тригонометричне рівняння, замінивши двійку тригонометричною тотожністю *2
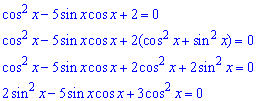
Перевіримо чи косинус може бути рівний нулю cos(x)=0.
Тоді 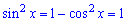 і при підстановці у задане рівняння (2≠0) бачимо, що cos(x)≠0.
і при підстановці у задане рівняння (2≠0) бачимо, що cos(x)≠0.
Це дає обґрунтування поділити усі члени рівняння на cos2(x):
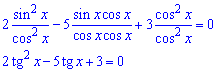
В такий спосіб приходимо до квадратного рівняння відносно тангенса.
Вводимо заміну tg(x)=u та через дискримінант обчислюємо корені
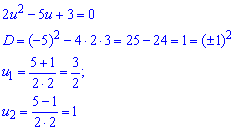
Обидва значення відповідають ОДЗ тангенса, тому після повернення до заміни матимемо два рівняння
tg(x)=3/2, tg(x)=1.
Далі використаємо знання про поведінку тангенса.
Оскільки функція tg(x) монотонно зростаюча на проміжку (-Pi/2;Pi/2), тобто при x0<x1 маємо tg(x0)<tg(x1), то tg(x0)=1, де x0- найменший додатній корінь рівняння cos2(x)-5sin(x)•cos(x)+2=0.
Відповідь: 1.
Приклад 18.49 Розв'язати рівняння
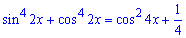
У відповідь записати значення 4•x0/Рі, де x0 - найменший додатний корінь рівняння.
Розв'язання: Знову задане тригонометричне рівняння четвертого порядку.
Для пониження степеня розпишемо четверту степінь як добуток других степенів, а далі використаємо основну тригонометричну тотожність для зведення до простого вигляду
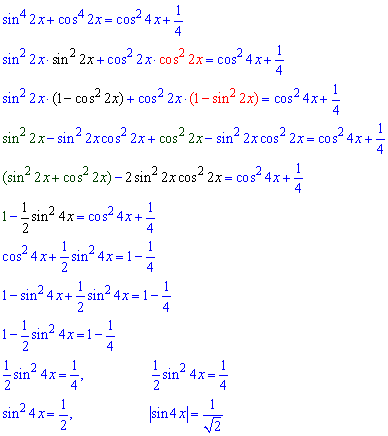
Отримане рівнянняз модулем, яке еквівалентне двом:
розв'язок першого має вигляд
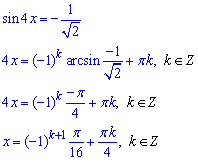
При k=1 маємо найменше додатне значення x=5•Pi/16.
Розкриття другого рівняння виконуємо за тією ж схемою
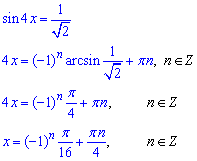
При n=0 маємо додатний мінімум x0=Pi/16.
Порівнявши значення робимо висновок, що x0=Pi/16 - найменший додатний корінь рівняння.
Наостанок нормуємо значення згідно умови 4x0/Pi=0,25.
Відповідь: 0,25.
Приклад 18.51 Розв'язати рівняння arcos(sin(x))=x/2.
У відповідь записати значення S/Pі, де S - сума всіх коренів рівняння.
Розв'язання: Шукати арккосинус від синуса звісно ніхто не буде, це нереально зробити аналітично.
Для розкриття рівняння до обох його частин застосовуємо косинус.
В результаті косинус від арккосинуса дасть сам аргумент, а в правій частині отримаємо косинус половини кута.
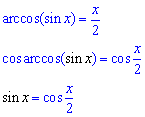
Далі щоб спростити ми синус в лівій частині рівності розписуємо за формулою синуса подвійного кута та переносимо всі вирази по один бік від знаку рівності, виносимо спільний множник.
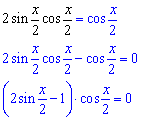
Розділяємо рівняння на два та розв'язуємо:
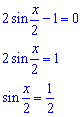
Оскільки синус симетричний відносно початку координат, то при розкритті отримаємо два значення кутів
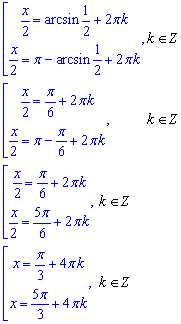
Корені другого рівняння приймають значення
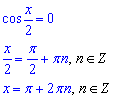
Далі підсумовуємо значення для k=0
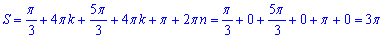 - сума всіх коренів рівняння.
- сума всіх коренів рівняння.
При додатніх та від'ємних номерах k сумувати немає змісту, оскільки корені взаємознищуються при сумуванні:
4Pi•k=0 , 2Pi•n=0.
Наостанок нормуємо на Рі:
S/Pi=3.
Відповідь: 3.
В завданнях складність полягає не в знаходженні найменшого додатного кореня, а в вивченні нових способів зведення складних тригонометричних рівнянь за допомогою тотожних перетворень. Це на перший погляд непідйомна мета, яка з практикою та обчисленням безлічі різноманітних рівнянь поступово досягається. Не надійтеся, що після прочитання наведених статтей Ви станете експертами в тригонометрії. Запевняємо Вас, що цього не станеться.
Наведені відповіді підказують, як обчислювати в тих чи інших випадках, які перетворення застосовувати.
Ваш рівень знань залежить лише від Вашого бажання працювати над собою, працювати самостійно, наполегливо і любити те, чим Ви займаєтеся.


