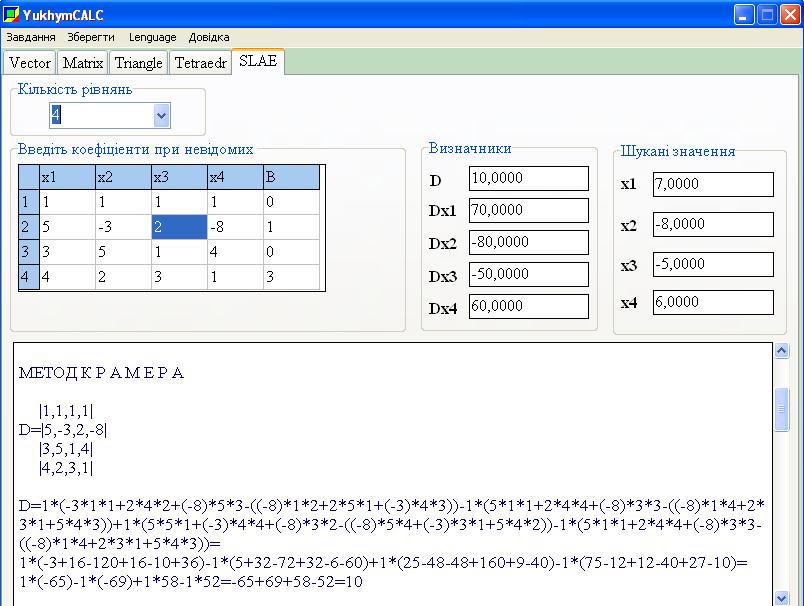
Задана система N лінійних алгебраїчних рівнянь (СЛАР) з N невідомими коефіцієнтами при яких є елементи матриці A(aij), а вільними членами є числа b1, b2, ..., bN
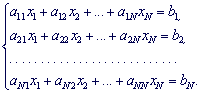
Перший індекс i біля коефіцієнтів aij вказує, в якому рівнянні знаходиться коефіцієнт, а другий j при якому із невідомих він знаходиться.
Якщо визначник матриці A не дорівнює нулю
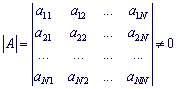
то система лінійних алгебраїчних рівнянь має єдиний розв'язок.
Розв'язком системи лінійних алгебраїчних рівнянь називається така впорядкована сукупність N чисел ![]() , яка при
, яка при ![]() перетворює кожне з рівнянь системи в правильну рівність.
перетворює кожне з рівнянь системи в правильну рівність.
Якщо праві частини всіх рівнянь системи дорівнюють нулю, то систему рівнянь називають однорідною. У випадку коли деякі з них відмінні від нуля – неоднорідною ![]()
Якщо система лінійних алгебраїчних рівнянь має хоч один розв'язок, то вона називається сумісною, в іншому випадку – несумісною.
Якщо розв'язок системи єдиний, то система лінійних рівнянь називається визначеною. У випадку, коли розв'язок сумісної системи не єдиний, систему рівнянь називають невизначеною.
Дві системи лінійних рівнянь називаються еквівалентними (або рівносильними), якщо всі розв'язки однієї системи є розв'язками другої, і навпаки. Еквівалентні (або рівносильні ) системи отримуємо з допомогою еквівалентних перетворень.
Еквівалентні перетворення СЛАР
1) переставлення місцями рівнянь;
2) множення (або ділення) рівнянь на відмінне від нуля число;
3) додавання до деякого рівняння іншого рівняння, помноженого на довільне, відмінне від нуля число.
Розв'язок СЛАР можна знайти різними способами. Розглянемо найпопулярніші методи.
МЕТОД КРАМЕРА
ТЕОРЕМА КРАМЕРА. Якщо визначник ![]() системи N лінійних алгебраїчних рівнянь з N невідомими відмінний від нуля
системи N лінійних алгебраїчних рівнянь з N невідомими відмінний від нуля ![]() , то ця система має єдиний розв'язок, який знаходиться за формулами Крамера:
, то ця система має єдиний розв'язок, який знаходиться за формулами Крамера:
![]()
![]() - визначники, утворений із
- визначники, утворений із ![]() заміною j-го стовпця, стовпцем із вільних членів.
заміною j-го стовпця, стовпцем із вільних членів.
Якщо ![]() , а хоча б один з
, а хоча б один з ![]() відмінний від нуля, то СЛАР розв'язків немає. Якщо ж
відмінний від нуля, то СЛАР розв'язків немає. Якщо ж ![]() , то СЛАР має безліч розв'язків. Розглянемо приклади з застосуванням методу Крамера.
, то СЛАР має безліч розв'язків. Розглянемо приклади з застосуванням методу Крамера.
Приклад 1. Дано систему трьох лінійних алгебраїчних рівнянь з трьома невідомими. Розв'язати систему за формулами Крамера.
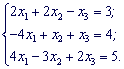
Розв'язок. Знайдемо визначник матриці коефіцієнтів при невідомих.
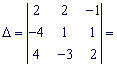
![]()
Так як ![]() , то задана система рівнянь сумісна і має єдиний розв'язок. Обчислимо визначники:
, то задана система рівнянь сумісна і має єдиний розв'язок. Обчислимо визначники:
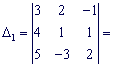
![]()
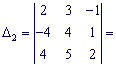
![]()
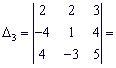
![]()
За формулами Крамера знаходимо розв'язок системи рівнянь
![]()
Отже x1=1; x2=3; x3=5 єдиний розв'язок системи.
Приклад 2. Дано систему чотирьох лінійних алгебраїчних рівнянь. Розв'язати систему за формулами Крамера
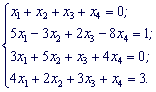
Розв'язок. Знайдемо визначник головної матриці системи. Для цього розкладемо його за першим рядком.
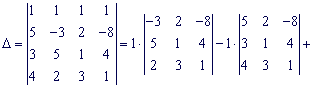
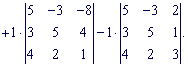
Знайдемо визначники третього порядку
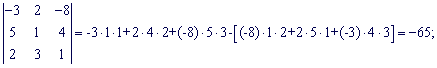
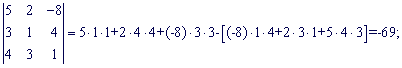
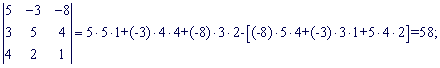
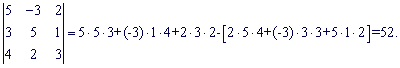
Підставимо знайдені значення у головний визначник
![]()
Визначник матриці не рівний нулеві ![]() , отже система рівнянь сумісна і має єдиний розв'язок. Шукаємо визначники за формулами Крамера
, отже система рівнянь сумісна і має єдиний розв'язок. Шукаємо визначники за формулами Крамера
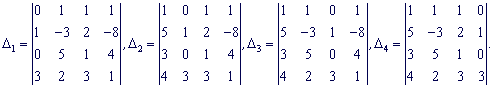
Розкладемо кожен з визначників через стовпець віьних членів, в ньому найбіьше нулів (2).
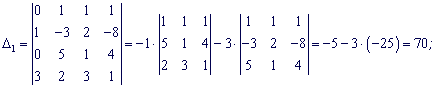
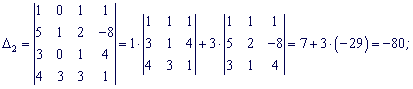
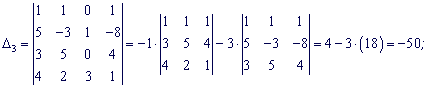
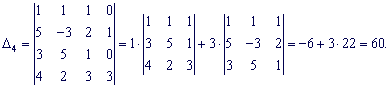
За формулами Крамера обчисюємо корені
![]()
Розв'язок системи x1=7; x2=-8; x3=-5; x4=6.
Даний приклад можна розв'язати програмою YukhymCalc . Фрагмент програми та результати обчислень системи рівнянь наведені нижче.
В результаті розв'язування системи лінійних рівнянь 4 поряду у тестовий файл Ви можете записати наступну відповідь.
МЕТОД КРАМЕРА
|1,1,1,1|
D=|5,-3,2,-8|
|3,5,1,4|
|4,2,3,1|
D=1*(-3*1*1+2*4*2+(-8)*5*3-((-8)*1*2+2*5*1+(-3)*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))+1*(5*5*1+(-3)*4*4+(-8)*3*2-((-8)*5*4+(-3)*3*1+5*4*2))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(-3+16-120+16-10+36)-1*(5+32-72+32-6-60)+1*(25-48-48+160+9-40)-1*(75-12+12-40+27-10)=1*(-65)-1*(-69)+1*58-1*52=-65+69+58-52=10
|0,1,1,1|
Dx1=|1,-3,2,-8|
|0,5,1,4|
|3,2,3,1|
Dx1=-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(1*5*1+(-3)*4*3+(-8)*0*2-((-8)*5*3+(-3)*0*1+1*4*2))-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))= -1*(1+24+0+24+0-12)+1*(5-36+0+120+0-8)-1*(15-9+0-30+0-2)= -1*(37)+1*81-1*(-26)=-37+81+26=70
|1,0,1,1|
Dx2=|5,1,2,-8|
|3,0,1,4|
|4,3,3,1|
Dx2=1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(1+24+0+24+0-12)+1*(0+16-72+0-3-60)-1*(0+4+18+0-9-15)= 1*37+1*(-119)-1*(-2)=37-119+2=-80
|1,1,0,1|
Dx3=|5,-3,1,-8|
|3,5,0,4|
|4,2,3,1|
Dx3=1*(-3*0*1+1*4*2+(-8)*5*3-((-8)*0*2+1*5*1+(-3)*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))= 1*(0+8-120+0-5+36)-1*(0+16-72+0-3-60)-1*(75+0+6-20+27+0)= 1*(-81)-1*(-119)-1*88=-81+119-88=-50
|1,1,1,0|
Dx4=|5,-3,2,1|
|3,5,1,0|
|4,2,3,3|
Dx4=1*(-3*1*3+2*0*2+1*5*3-(1*1*2+2*5*3+(-3)*0*3))-1*(5*1*3+2*0*4+1*3*3-(1*1*4+2*3*3+5*0*3))+1*(5*5*3+(-3)*0*4+1*3*2-(1*5*4+(-3)*3*3+5*0*2))= 1*(-9+0+15-2-30+0)-1*(15+0+9-4-18+0)+1*(75+0+6-20+27+0)= 1*(-26)-1*(2)+1*88=-26-2+88=60
x1=Dx1/D=70,0000/10,0000=7,0000
x2=Dx2/D=-80,0000/10,0000=-8,0000
x3=Dx3/D=-50,0000/10,0000=-5,0000
x4=Dx4/D=60,0000/10,0000=6,0000
Думаю, що Ви захочете мати такого помічника в себе на коп'ютері. Окрім наведених обчислень калькулятор має багато корисних функцій для роботи з матрицями, але це вже не відноситься до системи рівнянь.