Система лінійних рівнянь. Матричний метод

Маричний метод обчислення СЛАР не такий поширений як метод Крамера, однак він присутній в авчальній програмі з лінійної алгебри і його вивчають як один із способів розв'язання системи рівнянь.
Нехай маємо систему N лінійних алгебраїчних рівнянь (СЛАР) з N невідомими x₁, x₂,..., x_N.,коефіцієнтами при яких є елементи матриці A(a_ij), а вільними членами є числа b₁, b₂,..., b_N.

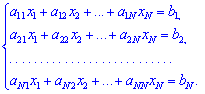
Позначимо через X – матрицю-стовпець невідомих, через B– матрицю-стовпець вільних членів. Тоді попередню систему рівнянь можна записати у вигляді матричного рівняння:
A*X=B
Якщо квадратна матриця A має відмінний від нуля визначник , то для неї існує обернена A^-1. Помноживши зліва в цьому рівнянні на A^-1, одержимо

Враховуючи, що добуток оберненої матриці на саму матрицю дає одиничну , а також формулу , одержимо матричний розв'язок системи
X=A^-1*B
Знаходження матричного розв'язку називається матричним способом розв'язування системи лінійних алгебраїчних рівнянь (СЛАР).

Приклад 1. Розв'язати систему лінійних рівнянь матричним методом.

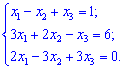
Розв'язок. Маємо систему з трьох рівнянь. Позначимо матрицю і вектори літерами

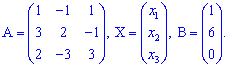
Матричний розв'язок системи алгебраїчних рівнянь шукаємо за формулою X=A^-1*B. Для знаходження оберненої матриці A^-1 обчислимо визначник


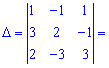
Оскільки він відмінний від нуля , то задана система рівнянь сумісна і має єдиний розв'язок.
Знайдемо транспоновану матрицю A

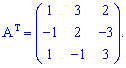
Обчислимо алгебраїчні доповнення до елементів заданої матриці:









Обернену матрицю отримаємо за формулою

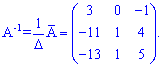
Знайдемо розв'язок СЛАР

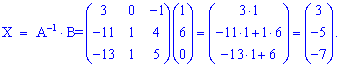
Розв'язок системи рівнянь x₁=3; x₂=-5; x₃=-7.
Розрахунки для системи із трьох рівнянь достатньо прості і зводяться на практиці до обчислень оберненої матриці, що теж не складно. У випадку системи чотирьох рівнянь обчислень буде куда більше і для визначення оберненої матриці доведеться шукати 16 визначників матриць розміром 3x3. Для системи рівнянь 5 порядку при визначенні оберненої матриці необхідно знаходити 25 визначників 4 порядку, або методом розкладу куда більше визначників 3 порядку. Перемножити обернену матрицю на праву частину рівняння після всіх операцій досить просто, і з цим справляються усі. Труднощі лише у обчисленні обернених матриць!