Метод Гауса розв'язування системи лінійних алгебраїчних рівнянь полягає в послідовному виключенні змінних і перетворенні системи рівнянь
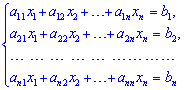
до трикутного (східчастого) вигляду
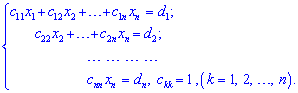
Припустимо, що в системі коефіцієнт при першому елементі відмінний від нуля ![]() . Якщо ця умова не виконується, то на перше місце переносимо рівняння, яке її задовільняє.
. Якщо ця умова не виконується, то на перше місце переносимо рівняння, яке її задовільняє.
За допомогою першого рівняння виключимо x1 із решти рівнянь.
Для цього ділять перший рядок на a11, позначимо це
![]()
Далі від другого рядка віднімаємо перший рядок, помножений на a21; від третього перший рядок, помножений на a31; і так далі до останнього рядка.
Дістанемо таблицю коефіцієнтів:

Для невідомих x2, .., xn маємо систему n-1 рівнянь. Виконуючи, як і раніше, виключимо x2 з усіх рівнянь, починаючи з третього. Для цього спочатку поділимо другий рядок на ![]() .
.
Якщо коефіцієнт ![]() , то переставимо рівняння так, щоб виконувалася умова
, то переставимо рівняння так, щоб виконувалася умова ![]() . Позначивши
. Позначивши
![]() ,
,
від третього рядка віднімемо другий рядок, помножений на ![]() ;
;
від четвертого рядка віднімемо другий рядок, помножений на ![]() і т.д.
і т.д.
Дістанемо таблицю коефіцієнтів:

Продовжуючи процес виключення невідомих отримаємо

таблицю коефіцієнтів при невідомих, яка має вигяд верхньої трикутної матриці. Всі елементи на головній діагоналі рівні одиниці ![]() . Запишемо відповідну систему рівнянь:
. Запишемо відповідну систему рівнянь:
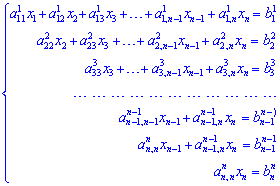
Перехід від першої системи рівнянь до останньої називається прямим ходом методу Гауса. Обернений хід методу Гауса починається з останньої системи рівнянь. Її розв'язують з кінця до початку. З останнього рівняння знаходять xn. Підставивши це значення в передостаннє – знаходять xn-1 і т.д. З першого рівняння знаходять x1.
Якщо система рівнянь з N невідомими має єдиний розв'язок, то ця система завжди може бути перетворена до трикутного вигляду. Для студентів не завжди вимагають, щоб діагональні елементи були рівні одиниці. Достатньо просто звести систему лінійних рівнянь до верхньої трикутної.
Приклад 1. Дано систему трьох лінійних алгебраїчних рівнянь з трьома невідомими. Розв'язати систему методом Гаусса.
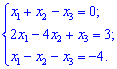
Розв'язок. Виключимо невідому x1 з другого і третього рівняння. Для цього від них віднімемо перше помножене на 2; 1:
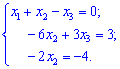
Бачимо, що наше рівняння в такому вигляді можна розв'язувати оберненим ходом методу Гауса. Для цього з останнього рівняння виразимо x2
![]()
Підставимо отримане значення в попереднє рівняння і знайдемо x3
![]()
З першого рівняння знаходимо x1
![]()
Розв'язок даної системи рівний x1 =3; x2=2; x3=5.
У випадках систем великих розмірів, а також для зручності, часто на практиці використовують іншу схему розв'язування. Замість перетворень над системою виконують відповідні перетворення над матрицею, складеною з коефіцієнтів при невідомих і стовпця з вільних членів, який для зручності виокремлюють вертикальною лінією. Таку матрицю ![]() називають розширеною матрицею системи.
називають розширеною матрицею системи.
Приклад 2. Розв'язати систему чотирьох лінійних алгебраїчних рівнянь методом Гаусса.
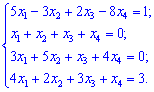
Розв'язок. Випишемо розширену матрицю для даної системи
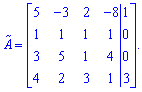
Зведемо її до трикутного вигляду з допомогою елементарних перетворень.
1. Поміняємо місцями перший і другий рядки.
2. Додамо до елементів другого, третього і четвертого рядків елементи першого рядка, помножені відповідно на -5; -3; -4.
3. Поміняємо місцями другий і третій рядки. Додамо до елементів третього і четвертого рядків елементи другого рядка, помножені відповідно на 4;1.
4. Від четвертого рівняння помноженого на 11 віднімаємо третє рівняння помножене на -3.
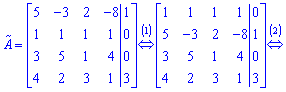
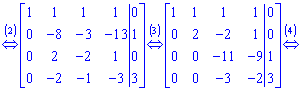
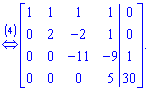
Такій розширеній матриці відповідає наступна система рівнянь
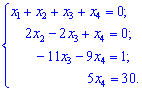
З четвертого рівняння знаходимо 4 невідому ![]() і підставляємо в третє рівняння
і підставляємо в третє рівняння
![]()
Знайдені значення підставляємо в друге рівняння
![]()
З першого рівняння знаходимо першу невідому
![]()
Системо повністю розв'язана і x1 =7; x2=-8; x3=-5; x4=-6 – її розв'язок.
Користуйтеся схемою Гауса де це вимагає умова завдання і використовуйте приведені схеми розрахунків.


