Всі студенти так чи інакше люблять коли в інтернеті зустрічаються готові відповіді контрольних чи індивідуальних робіт, зокрема і теорії рядів. Наведені нижче завдання задавали в Львівському національному університеті імені Івана Франка. Решта студентів теж багато візьмуть з наведених відповідей. Якщо не знайшли потрібного Вам матеріалу, то перегляньте інші статті з з категорії Ряди та їх збіжність. Матеріалу тут вдосталь, щоб підготуватись до контрольної чи тестів.
Завдання: 1.6 Обчислити суму рядів:
а)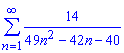 
Розв'язання: Обчисленням границі загального члена ряду
переконуємося, що даний ряд збігається.
Знайдемо його суму, для цього перетворимо загальний член таким чином, щоб мати суму чи різницю найпростіших дробів
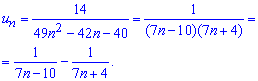
Це дасть можливість розкривати ряд через різницю наступних
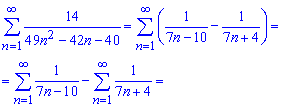
Розписавши останні ряди в явному вигляді, виділяємо доданки, які при обчисленні скоротяться. В результаті сума ряду рівна -1/12.
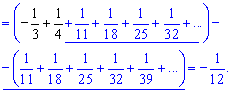
б)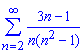 
Розв'язання: Знаходимо границю загального члена ряду
Вона рівна нулю, отже даний ряд збігається і є доцільними знаходження його суми. Для цього загальний член ряду методом невизначених коефіцієнтів. Схема розкладу ідентична до розкладу при інтегруванні дробових функцій
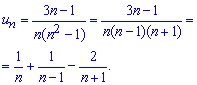
Це дозволяє спростити обчислення суми ряди і звести її до різниці трьох простих рядів
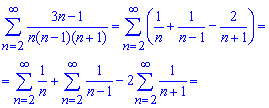
У випадку трьох рядів один з рядів при обчисленні пропадає (виділений червоним). Це слугує певною підказкою і показує скільки важливих (виділені чорним) доданків залишиться. Їх додаємо і отримуємо суму ряду, яка рівна 2.
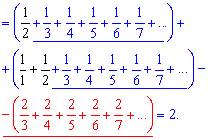
При обчисленнях вартує записувати суми рядів у стовпчик, як у формулах вище. Це допомагає швидко зорієнтуватися і відкинути доданки, які не вносять владу у суму.
Завдання: 2.17 Дослідити збіжність рядів:
а)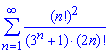 
Розв'язання: Оскільки даний ряд має додатні члени, то перевіряти його на збіжність будемо за допомогою ознаки Даламбера:
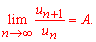
Для знаходження границі виписуємо загальний член ряду і наступний за ним
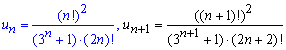
та підставляємо їх у формулу Даламбера. Для зручності аналізу чисельник дробу виділено чорним кольором.
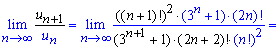
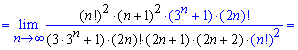
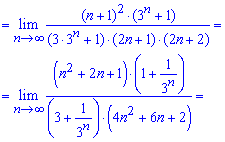
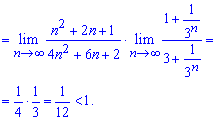
Границями 1/12 
, що є меншим за одиницю. За теоремою Даламбера даний ряд збігається!
б)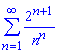 
Розв'язання: Для застосування ознаки Даламбера виконуємо обчислення границі частки старшого члена ряду до загального
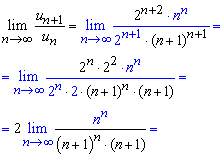
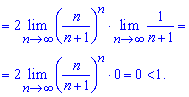
Границя рівна A=0<1, отже даний ряд збігається!
Завдання: 3.18 Знайти радіус збіжності та область збіжності степеневих рядів:
а)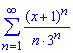 
Розв'язання: Для оцінки ряду складаємо ряд із модулів членів заданого ряду
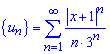
його загальний член запишемо формулу
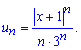
Оскільки даний ряд додатний, то досліджувати його збіжність будемо за ознакою Даламбера. Уважно розгляньте, як шукати границю за "n" для функціонального ряду
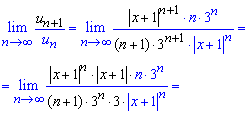
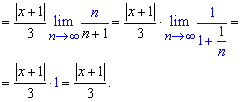
За теоремою Даламбера, якщо границя менша одиниці
то ряд збігається. Звідси маємо умову для визначення
- область збіжності ряду
та R =3 радіуса збіжності. У вигляді інтервалу область збіжності матиме наступне обмеження 
.
Радіус збіжності це по суті обмеження модуля (<3) при розкритті границі.
Розглянемо наступне завдання на збіжність ряду.
б)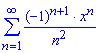 
Розв'язання: Даний ряд при від'ємних значеннях змінної приймає від'ємні значення, тому щоб застосувати теорему Даламбера складемо ряд із модулів членів заданого ряду
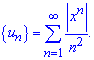
Тепер маємо додатний ряд і можемо перейти до обчислення границі частки членів ряду
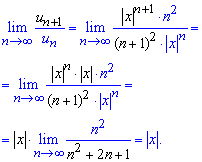
Отримали просте значення границі. За теоремою Даламбера ряд буде збіжним, якщо |x|<1. Звідси маємо умову для визначення
- області збіжності ряду та R=1 - радіуса збіжності.
Завдання: 4.19 Розкласти функцію в ряд по степенях x:
Розв'язання: Спочатку спростимо залежність, а потім розкладемо цю функцію в ряд по степенях x, скориставшись однією з відомих формул Маклорена:
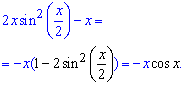
Оскільки розклад косинуса в ряд відомий і має вигляд
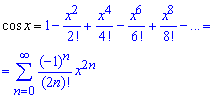
то розлад заданої функції запишемо формулою
Це не надто складне завдання, оскільки відповіді до інших варіантів контрольної по рядах більш громіздкі.
Завдання: 5.20 Розкласти арксинус функцію в ряд по степенях x:
Розв'язання: Для розкладу функції в ряд використаємо наступну методику. Знайдемо похідну від складеної функції
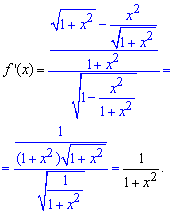
Далі розкладемо похідну 
в ряд, скориставшись однією з формул Маклорена для степеневих залежностей:
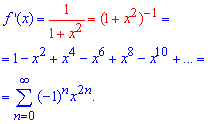
Проінтегрувавши почленно цю залежність, отримаємо розклад заданої функції в ряд по степенях x:
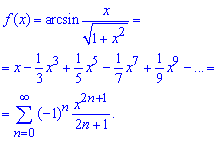
Деталей інтегрування ми не розписували, оскільки похідна має достатньо просте розвинення ряд і подібні інтеграли на практиці Ви знаходили досить часто.
Завдання: 6.21 Розкласти функцію в тригонометричний ряд Фур'є:
Розв'язання: Формули розкладу в ряд Фур'є можете взяти з попередніх статей. Суть розкладу зводиться до обчислення коефіцієнтів Фур'є інтегруванням
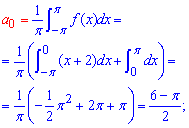
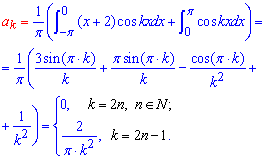
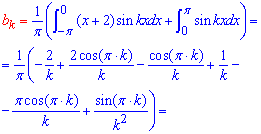
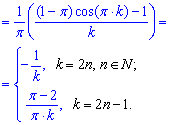
Далі їх підставляємо в формулу Фур'є. Це і буде тригонометричним розкладом функції
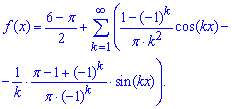
Складність обчислень полягає в тому, що коефіцієнти Фур'є для парних і непарних номерів потрібно звести в єдину формулу. Якщо цього не зробити, то компактного вигляду ряду, як у відповіді Ви не отримаєте. Цього вчать на практичних заняттях з вищої математики, хоча не всім студентам це вдається.
Що стосується заочного навчання то студенти-заочники мають ще менші шанси оволодіти даною методикою обчислень.
