Область збіжності степеневого ряду

За теоремою Абеля, якщо ряд a_n=c_n·xⁿ збігається в точці x1 то він збігається абсолютно для всіх "іксів" по модулю менших за |x1|

Наслідком з теорем Абеля є те, що при "іксах" менших радіуса збіжності R ряд абсолютно збіжний, при |x|>R ряд розбігається і при x=-R, x=R потрібні додаткові дослідження. Більше теорії про радіус збіжності та область збіжності степеневих рядів Ви можете ознайомитися за посиланням. Нижче приведені формули радіуса збіжності ряду за ознакою Д'Аламбера та радикальною ознакою Коші.

Переходимо до практичних та детально пройдемо алгоритм знаходження радіуса степеневого ряду, а за ним і самої області збіжності.

Приклад 1. Знайти область збіжності степеневого ряду

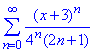
Розв'язування: Виписуємо два послідовних члени ряду, підставляємо в формулу області збіжності та розписуємо границю за д'Аламбером

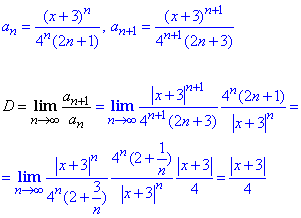
Згідно з теорією, отримана границя за модулем повинна бути менша одиниці
|x+3|/4<1,
|x+3| -4<x+3<4
-4-3<x<4-3
-7<x<1
x∈(-7;1) – область збіжності степеневого ряду.
Окремо слід розібрати граничні випадки.
При x=1 отримаємо ряд близький за поведінкою до гармонічного (a_n=1/n), тому він розбіжний.
При x=-7 загальний член заданого ряду набуде вигляду
b_n=(-1)ⁿ/(2n+1).
Члени ряду з модулів монотонно спадають + границя n-го члена прямує до нуля, тому за ознакою Лейбніца він збіжний.
Ця збіжність не абсолютна, а умовна, оскільки ряд складений з модулів розбіжний.
Тому остаточно у відповідь слід записати
x∈[-7;1) – область збіжності степеневого ряду.

Приклад 2. Визначити радіус збіжності та область збіжності функціонального ряду

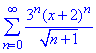
Розв'язування: Повторюємо алгоритм обчислень

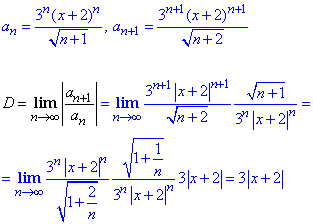
За формулою Даламбера, щоб ряд був збіжним, необхідно щоб знайдена границя по модулю не перевищувала 1.
Звідси розписуємо нерівність з модулем
3|x+2|<1,
|3x+6|<1,
-1<3x+6<1,
-1-6<3x<1,
-6 -7<3x<-5,
-7/3<x<-5/3.
x∈(-7/3;-5/3).
Перевіримо крайні точки.
При x=-5/3 загальний член ряду перетворюєтья до вигляду a_n=1/√(n+1), що є рядом Діріхле з показником степеня p=1/2<1.
Тому такий числовий ряд розбіжний.
При x=-7/3 отримаємо знакозмінний ряд a_n=(-1)ⁿ⁺¹/√(n+1), який за модулем монотонно спадає і прямує до нуля при спрямуванні номера до безмежності.
Такий ряд за ознакою Лейбніца є збіжним.
Радіус збіжності рівний R=(-5/3+7/3)/2=1/3,
x∈[-7/3;-5/3) – область збіжності функціонального ряду.
Це найповніше обґрунтування до умови прикладу.

Приклад 3. Визначити область збіжності ряду

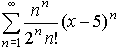
Розв'язування: Запишемо загальний вигляд степеневого ряду

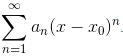
Центр області збіжності x₀=5.

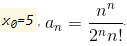
Область збіжності степеневого ряду визначається радіусом збіжності R:
|x-x0|<R або x0-R<x<x0+R
Збіжність ряду на границях (при x=x0±R) необхідно досліджувати додатково.
Знайдемо радіус збіжності ряду за формулою д'Аламбера:

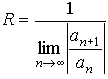
Виписуємо члени ряду та знаходимо границю їх відношення

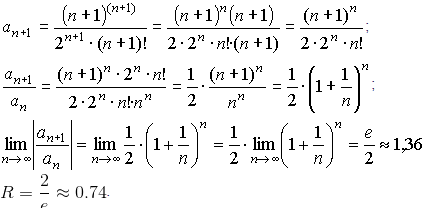
Перевіримо збіжність ряду на правому краю
x=5+2/e.
Підстановкою x в заданий ряд, отримаємо

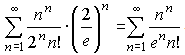
Для дослідження ряду використаємо формулу Стірлінга , справедливу для факторіалів великих чисел

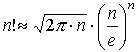
Отримаємо ряд для застосування ознаки порівняння, який є розбіжним
Дослідимо збіжність ряду при x=5-2/e.
При підстановці x=5-2/e в 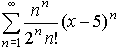отримаємо знакозмінний числовий ряд

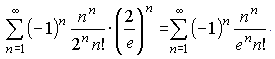
При застосуванні формули Стірлінга дістанемо ряд для порівняння

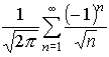
Цей ряд є збіжним за ознакою Лейбніца, хоча й умовно, оскільки для ряду з модулів степінь знаменника p=1/2<1, тому абсолютний ряд розбігається.
Тому ліву границю включаємо в область збіжності степеневого ряду:

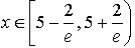
Запам'ятайте, що найшвидше перевірити збіжність ряду можна на лівій границі області. Якщо в ній отриманий знакозміннний ряд умовно збіжний, то цю точку включаємо, а праву границю не включаємо
x0-R≤x<x0+R .
Якщо на лівій границі області збіжності ряд абсолютно збіжний то праву границю також включаємо
x0-R≤x≤x0+R.

Приклад 4. Довести, що радіус збіжності ряду рівний 5/3 та визначити чи входять краї в область збіжності ряду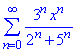

Розв'язування: За формулою  Даламбера знаходимо радіус збіжності

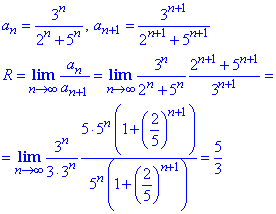
Таким чином отримали R=5/3, і степеневий ряд абсолютно збіжний на інтервалі (-5/3;5/3).
перевіримо збіжність на краях.
Для цього дослідимо лівий край x=-5/3.
При підстановці вихідний ряд прийме вигляд

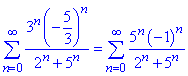
Отриманий знакозмінний ряд монотонно спадає за абсолютною величиною, однак не прямує до нуля при змінній прямуючій до безмежності

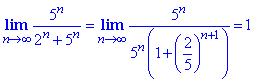
За ознакою Лейбніца ряд розбіжний.
Таку ж границю отримаємо на правому краю області збіжності.
Звідси робимо висновок, що крайні точки не входять в область збіжності ряду.
Остаточно отримали, що степеневий ряд збіжний в інтервалі
x∈(-5/3;5/3).
На цьому всі доведення та дослідження до умови виконані.

Приклад 5. Знайти область збіжності ряду

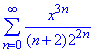
Розв'язування: До ряду складеного з модулів a_n=x^3n/((n+1)*2^2n) застосуємо ознаку Даламбера:

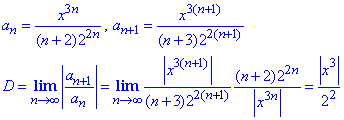
При |x|^3/4<1 степеневий ряд збігається абсолютно.
Звідси випливає, що радіус збіжності рівний коренію кубічному з чотирьох
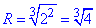, а інтервалом збіжності ряду є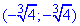
На кінцях інтервалу збіжності:
при 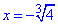запишемо чому рівний ряд

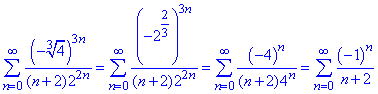
Це знакозмінний ряд, який за модулем монотонно збігається і границя n-го члена прямує до нуля, тому за ознакою Лейбніца ряд збіжний.
Ця збіжність умовна, тому що ряд складений з модулів u_n=1/(n+2) розбігається як гармонічний ряд.
Тому лівий край в область збіжності степеневого ряду включаємо, а правий ні:
Остаточно, 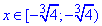- область збіжності степеневого ряду.
Якщо б викладач питав, чому так, то слід обґрунтувати, що умовної збіжності за Лейбніцом достатньо, щоб включити ліву границю області збіжності в розв'язок.

Таких прикладів ми розв'язуємо десятками, допомагаючи студентам на екзаменах та розрахункових. Крок за кроком вивчайте наведені в категорії Ряди теми і з часом у Вас не буде питань на практичних чи іспитах.