Диференціальні рівняння даються легко не всім студентам, для їх обчислень потрібно володіти добрими знаннями з інтегрування. Решта все зводиться до технічних прийомів, які добре розписані в теорії, та зводяться під певні алгоритми дій. Для рівнянь з відокремленими змінними та звідними до них основна задача полягає в розділенні змінних, хоч вона і не складна. Інтегрування вважають простим етапом розрахунків, хоча практика показує що все з точністю до навпаки. Наведені далі приклади будуть корисними для студентів ВУЗ-ів на практичних, модулях, екзаменах.
Завдання, що тут розписані взяті із збірника задач з курсу «Диференціальні рівняння». Бокало М. М (ЛНУ ім. І. Франка).
Рівняння з відокремлюваними змінними та звідні до них
Приклад 1.23 Розв'язати диференціальне рівняння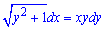 
Розв'язання: Перенесемо всі доданки в ліву сторону і отримаємо ДР в симетричній формі:
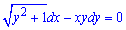
Розділивши обидві частини рівняння на добуток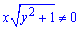 
, отримаємо рівняння з відокремленими змінними
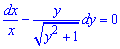
Проінтегруємо останнє рівняння
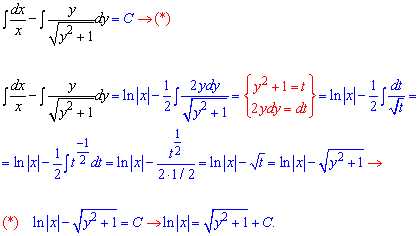
Щоб розкрити другий інтеграл використали заміну змінних
y2+1=t, 2y*dy=dt.
Крім цього, розв'язками заданого диференціального рівняння можуть знаходитись серед виразів, на які ми ділимо, тобто x=0.
Підстановка в початкове рівняння підтверджує, що x=0 є особливим розв'язком ДР.
Отже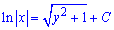 
і x=0 - загальний інтеграл диференціального рівняння.
Приклад 1.26 Розв'язати задачу Коші для диференціального рівняння
y'=3y2/3, y(2)=0.
Розв'язання: Розписуємо похідну функції та відокремлюємо змінні.
Далі застосовуємо невизначений інтеграл та проводимо обчислення
(*)
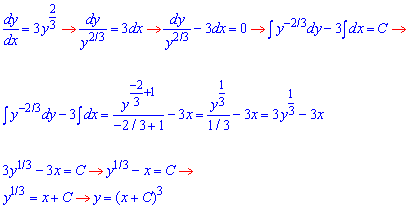При розділенні змінних ділили на y, тому прирівнюємо його до нуля і перевірити чи при цьому початкове ДР перетворюється в тотожність. В даному прикладі y=0 є особливим розв'язком диференціального рівняння.
Підсумовуючи все вище, маємо y=(x+С)3 і y=0 - два загальні розв'язки рівняння.
Далі розв'язуємо задачу Коші, тобто задовільнимо початкову умову y(2)=0:
0=(2+C)3 , звідси C=-2.
Отож, підставляємо сталу С в рівняння (*), та записуємо розв'язок задачі Коші:
y=(x-2) 3.
Приклад 1.28 Розв'язати диференціальне рівняння 2x2yy'+y2=2
Розв'язання: Перетворимо наведену диференційну залежність до ДР з відокремленими змінними. Далі інтегруванням обчислюємо загальний розв'язок диференціального рівняння. Більше інформації про проміжні обчислення дають наступні формули
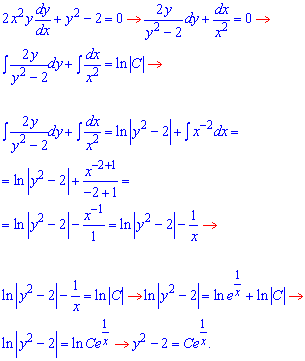
Врахуємо, що вираз на який ділили теж може бути розв'язком ДР.
Тоді y2-2=0, звідси два значення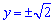 
.
Можемо зауважити, що ці ж значення коренів отримаємо при C=0, тому вона входить в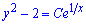 
- загальний розв'язок рівняння.
Приклад 1.31 Розв'язати диференціальне рівняння z'=10x+z.
Розв'язання: Враховуючи властивості показників, розписуємо показникову частину та зводимо до ДР з розділеними змінними.
Далі інтегруванням знаходимо розв'язок ДР
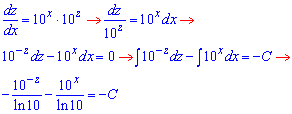
Дану відповідь можна спростити, внісши знаменник ln(10) під сталу.
В результаті отримаємо
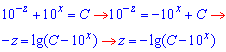
загальний розв'язок рівняння у явному вигляді.
Приклад 1.36 Знайти розв'язок задачі Коші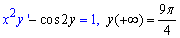 
Розв'язання: Маємо ДР першого порядку. Спершу позбудемося неоднорідності, для цього косинус подвійного аргументу розпишемо за тригонометричною формулою.
Далі розділяємо змінні та інтегруванням знаходимо розв'язок ДР у явному вигляді
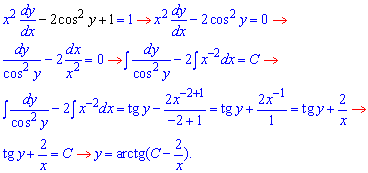
Також врахуємо множник на який ділили рівняння cos2(y), він також буде розв'язком ДР:
cos2(y)=0, звідси
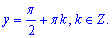
Остаточно отримали
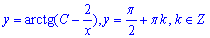- загальний розв'язок рівняння.
Задовільнимо умову Коші:
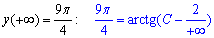
звідси C=1.
Отож, розв'язок задачі Коші прийме значення
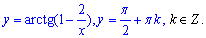
Приклад 1.37 Знайти розв'язок ДР 3y2y'+16x=2xy3, y(x) - обмежена при змінній прямуючій до безмежності 
.
Розв'язання: Алгоритм обчислень полягає в розділенні змінних, а це не завжди легко бачити. В одних випадках достатньо винести спільний множник за дужки, в інших застосувати властивості показникових чи тригонометричних функцій. Підходи в кожному випадку різняться, головна мета – розділити змінні, щоб біля dx мали змінні в чисельнику чи знаменнику від x, при dy функцію від y.
Лише тоді маємо право до обох частин застосувати невизначений інтеграл
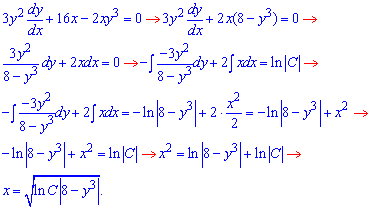
Тут простіше було виразити явний вигляд оберненої функції x(y).
Обов'язково перевіряйте на рівність нулю множник на який ділили при розділенні змінних.
В цьому завданні матимемо умову 8-y3=0, звідси y=2 - особливий розв'язок ДР.
Звідси y=2 - входить до загального розв'язку рівняння, крім цього задовольняє умову Коші.
Приклад 1.39 Розв'язати задачу Коші для ДР
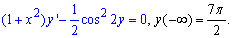
Розв'язання: Розділимо змінні в диференціальному рівнянні, після чого інтегруємо його
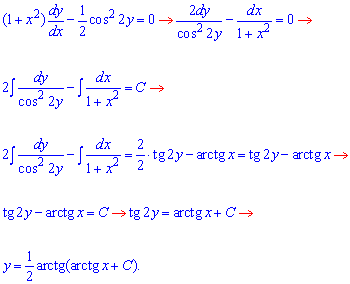
Перевіримо множник на який виконували ділення.
Отримаємо cos2(y)=0,
звідси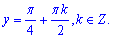 
Тому
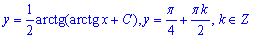
загальний розв'язок рівняння.
Задовільнимо умову Коші
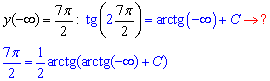
звідси C=Pi/2.
Отож, розв'язок задачі Коші:
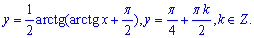
Приклад 1.43 Знайти загальний розв'язок ДР
y'-y=2x-3
Розв'язання: Переносимо змінну в праву частину y'=y+2x-3, далі виконуємо заміну змінних z=y+2x-3, тоді y'+2=z', звідки похідна y'=z'-2, z'-2=z, z'-2-z=0.
Проводимо інтегрування ДР
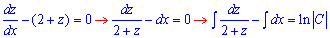
ln|2+z|-x=ln|C|,
ln|2+z|=ln(ex)+ln|C|,
2+z=Cex,
z= Cex-2.
Повернемося до початкових змінних:
y+2x-3= Cex-2,
y= Cex-2x+1.
Врахуємо, що ділили на вираз
2+z=0 маємо z=-2,
звідки y+2x-3=-2, y=1-2x
Однак таке значення отримаємо при С=0 із загальної формули.
Тому y= Cex-2x+1 - єдиний розв'язок диф. рівняння.
Приклад 1.44 Розв'язати задачу Коші
(x+2y)y'=1, y(0)=-1.
Розв'язання: Тут необхідно застосувати заміну x+2y=z (*), тоді 1+2y'=z', звідки
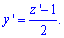
Підставляємо в початкову залежність
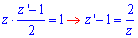
Далі зводимо до рівняння з відокремленими змінними та інтегруємо останнє
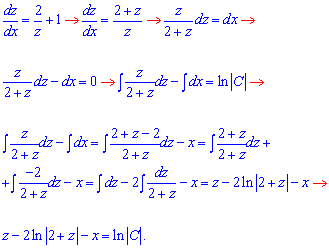
Повернемося до початкових змінних:
x+2y-2ln|2+x+2y|-x=ln|C|,
2y-2ln|2+x+2y|=ln|C|,
ln(ey)=ln|C(2+x+2y)|,
ey=C(x+2y+2).
Врахуємо, що 2+z=0, звідси z=-2, звідки (*) ще одне рішення x+2y+2=0.
ey=C(x+2y+2), x+2y+2=0 - загальний розв'язок рівняння.
Розв'яжемо задачу Коші y(0)=-1:
e-1=C(0-2+2), звідси стала не існує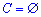 
.
Отож, розв'язок задачі Коші:
x+2y+2=0.
Приклад 1.46 Знайти загальний інтеграл диф. р-ня
y'=sin(x-y).
Розв'язання: Зробимо заміну x-y=z, тоді 1-y'=z', звідки y'=1-z',
1-z'=sin(z), z'=1-sin(z)
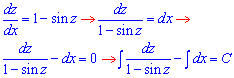
При інтегруванні треба використати заміну
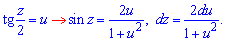
тоді і. (через громіздкі записи, цей інтеграл не розписую детально). (*)
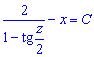
Повернемося до початкових змінних:
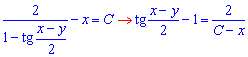
Врахуємо, що 1-sin(z)=0, звідси
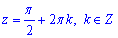, звідки
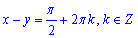
Підсумовуючи всі обрахунки запишемо загальний інтеграл ДР
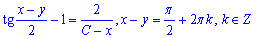
Приклад 1.47 Знайти загальний інтеграл диф. р-ня (x+y)2y'=a2,
Розв'язання: Заміна змінних для диференціального р-ня наступна
x+y=z, тоді 1+y'=z', звідки y'=z'-1.
При цьому початкове рівняння перетвориться до вигляду
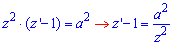
Записуємо рівняння в диференціалах, розділяємо змінні та переходимо до інтегрування
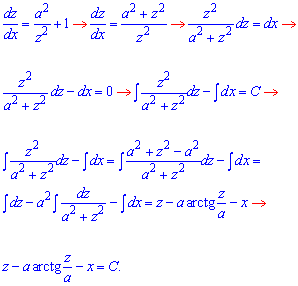
В формулі вище описані всі маніпуляції з підінтегральними функціями, що дозволяє напряму застосувати табличні інтеграли. На цьому не будемо наголошувати, але для себе аналізуйте та вивчайте наведені прийоми. Таким чином не тільки навчитеся розв'язувати диф. р-ня, а й отримаєте досвід інтегрування.
Повернемося до початкових змінних:
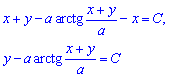або
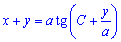- загальний розв'язок рівняння.
Приклад 1.84 Знайти загальний інтеграл ДР (x-2y-1)dx+(3x-6y+2)dy=0,
Розв'язання: Перетворимо ДР до наступної форми
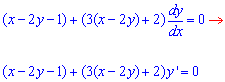
Це дозволяє застосувати наступну заміну змінних
x-2y=z, тоді 1-2y'=z', звідки y'=(1-z')/2.
Розпишемо ДР
z-1+(3z+2)(1-z')/2=0,
2(z-1)+(3z+2)(1-z')=0,
2z-2+3z-2-(3z+2)z'=0.
Далі переходимо до рівняння з відокремленими змінними та виконуємо інтегрування
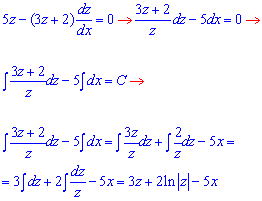
3z+2ln|z|-5x=C.
Отриманий розв'язок записаний в нових змінних, тому необхідно перейти до початкових:
3(x-2y)+2ln|x-2y|-5x=C. або ln|x-2y|=x+3y+C.
Врахуємо множник на який ділили початкове ДР, з умови z=0 маємо x-2y=0 особливий розв'язок ДР.
Тому отримали ln|x-2y|=x+3y+C, x-2y=0 - загальний розв'язок рівняння.
Приклад 1.86 Знайти загальний інтеграл ДР (x-2y+1)dx-(2x+4y+3)dy=0,
Розв'язання: Маємо ще одне задання, подібне до попереднього.
Запишемо ДР через похідну
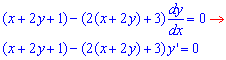
Заміна змінних x+2y=z, 1+2y'=z',y'=(z'-1)/2
зведе початкове ДР до наступного
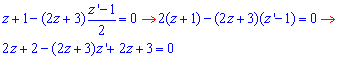
Далі розділяємо змінні та інтегруємо рівняння з відокремленими змінними
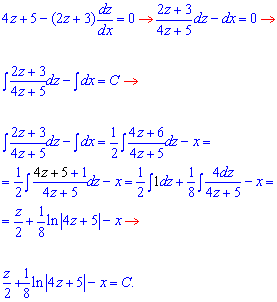
ln|4z+5|=8x-4z+C.
Повернемося у відповіді від z до x, y:
ln|4(x+2y)+5|=8x-4(x+2y)+C,
ln|4(x+2y)+5|=4x-8y+C.
Врахуємо значення на яке ділили. Прирівнюємо до нуля
4z+5=0
і переконуємося що пряма 4x+8y+5=0 є особливим р-ком ДР
Тому 2 р-ня ln|4(x+2y)+5|=4x-8y+C, 4x+8y+5=0 складають загальний інтеграл диференціального рівняння.
Для вивчення даної теми рекомендумаємо самостійно вправлятися з подібними завданнями і вправлятися багато.
На початкових етапах можете не інтегрувати диференціальне рівняння, просто вивчити всі можливі прийоми та заміни змінних, що дозволяють отримати ДР з відокремленими змінними.
Далі можна рухатися в сторону інтегрування диференціальних рівняннь та задовільнення крайових умов (задачі Коші), якщо такі задані.
