На попередньому уроці детально розібрали метод Бернуллі, оцінили його ефективність в розв'язуванні лінійних ДР першого порядку та обчислили кілька прикладів. сьогодні тільки практика і за допомогою формул покажемо як відбувається розділення ДР на два ДР з відокремленими змінними.
Приклади та схеми доволі прості тому Ви швидко зможете вивчити тему самостійно.
Приклад 1. Знайти розв'язок диференціального рівняння
y'-4y/x=2x2*√y
Розв'язування: Маємо диференціальне рівняння Бернуллі з показником y вправій частині рівним m=1/2 або 0,5 (корінь квадратний від y).
Розв'язок шукаємо у вигляді добутку двох функцій, які визначаємо інтегруванням двох відповідних ДР з відокремленими змінними.
Деталі методу Бернуллі наведені в формулах нижче
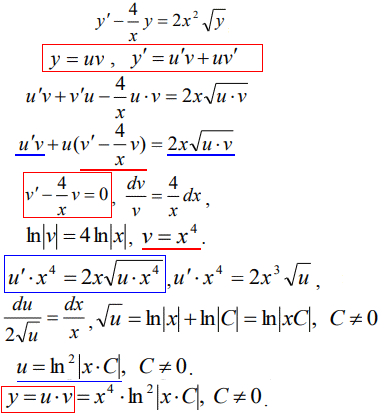
Уважно перегляньте, як можна сталу внести під логарифм.
Такий прийом часто застосовують при обчисленнях, щоб спростити подальші перетворення функцій.
Також, слід зазначити, що y=0 - є особливим розв'язком заданого ДР.
В цьому легко переконатися, підставивши його у вихідне рівняння.
Приклад 2. Розв'язати рівняння
y'+y/x=-x*y2.
Розв'язування: В правій стороні маємо "ігрик" у квадраті, тому задане лінійне неоднорідне диференціальне рівняння (ЛНДР) є рівнянням Бернуллі.
Його розв'язок y(x) подаємо у вигляді добутку двох функцій y(x)=u(x)*v(x), диференціюємо та підставляємо у вихідне ДР, розділяючи його на 2 ДР відповідно методики описаної на попередньому уроці.
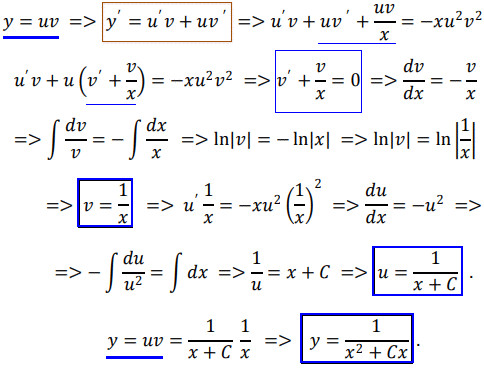
Остання формула це і є шуканийзагальний розв'язок диф. р-ня.
Приклад 3. Знайти розв'язки рівняння
xy2*y'=x2+y3
Розв'язування: Розділяємо обидві частини р-ня на множник перед y', та переносимо один доданок в праву сторону.
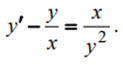
Дане ДР за допомогою заміни z=y^3 можна звести до лінійного, але у нас мета - навчитися застосовувати метод Бернуллі, тому розв'язок подаємо у вигляді добутку двох функцій, які знаходимо інтегруванням, розв'язуючи відповідні ДР.
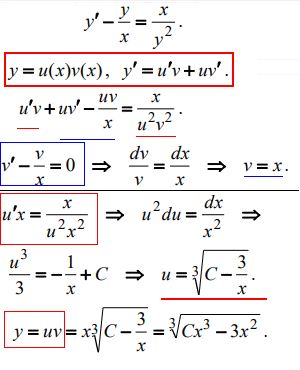
Тут і надалі в формулах позначатимемо вирази, які формують кожне з двох ДР та відповідні їм розв'язки.
Так Вам швидше запам'ятається алгоритм Бернуллі, а самі розв'язування ДР не важкі, оскільки, як правило, доводиться інтегрувати табличні або близькі до них функції.
Приклад 4. Розв'язати ДР
x^2*y^2*y'+x*y^3=a^2,
де a - довільна стала.
Розв'язування: Поділимо рівняння на множник при y', щоб було явно видно, що маємо диференціальне рівняння Бернуллі з показником y правій частині рівним m=-2.
Застосовуємо метод Бернуллі - розв'язок шукаємо у вигляді добутку двох функцій, які встановлюємо, розв'язуючи відповідні ДР.
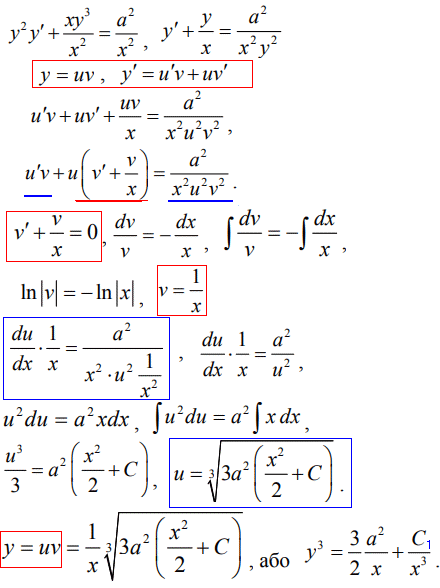
Тут при інтегруванні отримали функцію u(x) в кубі, тому для підстановки в кінцеву формулу брали її корінь кубічний.
Буває, що при інтегруванні вона міститься в експоненті, під гогарифмом або коренем, тому будьте готові її добувати та обчислювати подібні інтеграли.
Приклад 5. Розв'язати рівняння Бернуллі
y'+y/x=2ln(x)*y2/x.
Розв'язування: Маємо ДР Бернуллі з показником y вправій частині рівним m=2.
Подаємо розв'язок у вигляді добутку 2 функцій, підставляємо в ДР та за схемою Бернуллі - розділяємо на два ДР з відокремленими змінними, які по черзі інтегруємо:
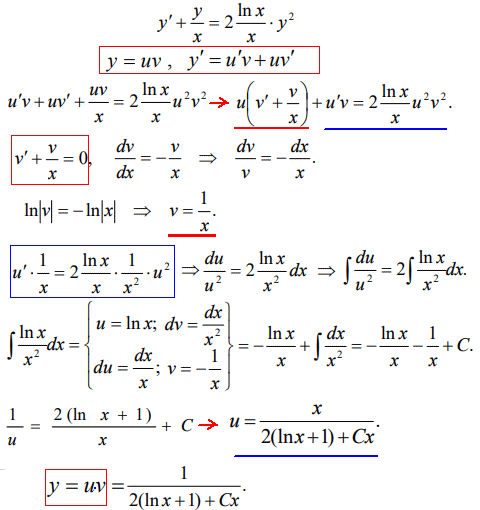
Уважно перегляньте інтегрування в другому ДР, тут довелося застосовувати інтегрування частинами, щоб знайти відповідний інтеграл.
Наприкінці уроку нами відібрані приклади на ДР Бернуллі для самостійного розв'язання. Спробуйте свої знання, щоб бачити чи дійсно Ви зрозуміли схему Бернуллі та чи зможете її самостійно повторити на практичних.
Приклад 6. Знайти розв'язок задачі Коші для диференціального рівняння
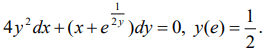
Розв'язування: Бачимо, що рівняння відносно y(x) є нелінійним, тоді як перехід до x(y) перетворює його на лінійне неоднорідне ДР, причому в даному прикладі зводить до рівняння Бернуллі відносно x(y).
Тому подаємо x(y) як добуток двох функцій від "ігрик", та за схемою Бернуллі шляхом інтегруванням знаходимо їх.
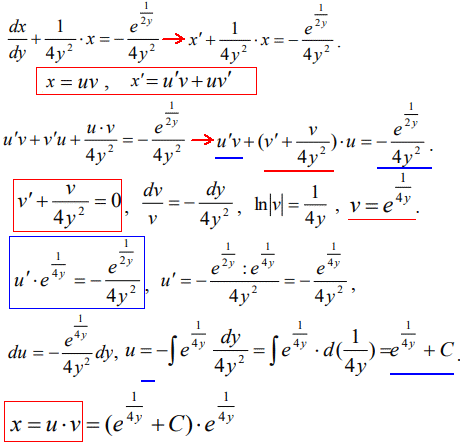
Останній рядок є загальним розв'язком ДР Бернуллі.
Далі, щоб задовільнити умову Коші потрібно, щоб крива x(y) проходила через точку (e, 1/2), тобто при x=e, y=1/2.
Підставляємо та знаходимо сталу С.
e=(e^1/2+c)*e^1/2,
Звідси C=0.
Тоді x=e1/4y*e1/4y=e1/2y - частинний розв'язок заданого ДР.
Приклад 7. Звести до рівняння Бернуллі та обчислити
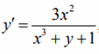
Розв'язування: Для перетворення рівняння запишемо
y'=dy/dx=1/(dx/dy)=1/x'.
Таким чином від похідної y' пререйдемо до x'(y).
Раніше писали, що немає різниці в якому вигляді шукати розв'язок, головне - ДР звести до відомого типу, методику обчислення якого знаємо.
При перетворенні отримаємо диференціальне рівняння Бернуллі з показником y вправій частині рівним m=-2
(див. степінь "ікса" в правій частині за знаком рівності).
Далі у формулах наведені основні переходи та саме інтегрування ДР.

В такому неявному вигляді можемо залишити загальний інтеграл диф. р-ня, а можна за бажанням виразити явний вигляд функції x=x(y).
Приклад 8. Знайти загальний розв'язок диференціального рівняння
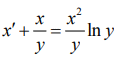
Розв'язування: Задано ДР Бернуллі відносно функції x(y) порядку m=2.
Розв'язок подаємо через добуток функцій, розділяємо ДР на два ДР з відокремленими змінними та по черзі розв'язуємо їх.
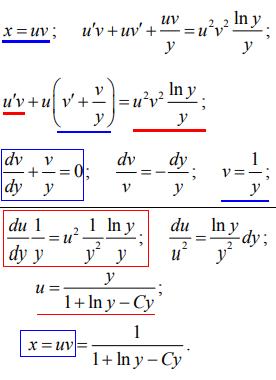
Тут опущені знаки інтегрування, але Вам і так зрозуміло, що і як робити, щоб розв'язати рівняння з відокремленими змінними.
Наостанок, для закріплення на практиці теми, розв'яжіть самостійно кілька завдань на схему Бернуллі + умову Коші ( за бажанням):
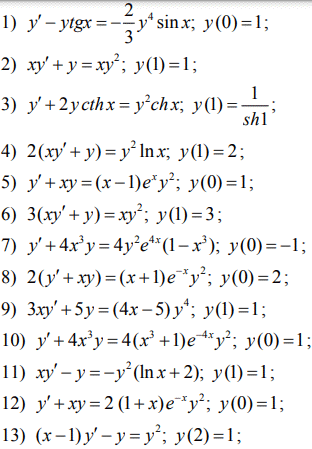
Якщо маєте труднощі з ДР то допоможемо консультаціями щодо правильності обчислень.
Звертайтеся, ми відкриті до співпраці та постійно підтримуємо студентів у навчанні!


