Продовжуємо тему ДР першого порядку і сьогодні розглянемо готові приклади на лінійні диференціальні рівняння 1 порядку розв'язні методом Бернуллі. Суть методу полягає в поданні розв'язку у вигляді добутку двох функцій та розділенні ДР за рахунок цього на два прості ДР з відокремлюваними змінними. Детально метод розписаний раніше, тут його ефективність буде показано при обчисленнях, тому ваше завдання швидко запам'ятати метод Бернуллі, щоб в подальшому могти вільно повторити до подібних ДР першого порядку.
Приклад 1. Знайти розв'язок диференціального рівняння
y'-2y/x=2x3.
Розв'язування: З вигляду бачимо, що задано лінійне диференціальне рівняння першого порядку.
Це не є рівняння Бернуллі, оскільки в правій стороні немає "ігрика" в будь-якому степені за вийнятком m=0 та m=1.
Однак і для такого типу рівнянь алгоритм Ейлера-Бернуллі добре підходить.
Перегляньте хід розв'язування ДР з наступних формул.
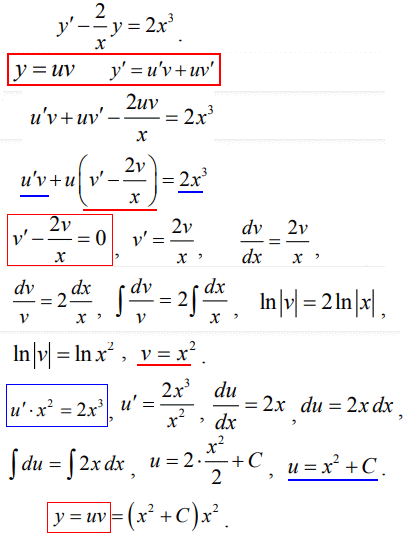
Вкінці ре забувайте, що розв'язок - це добуток двох функцій, тому в такому вигляді його і записуйте.
Приклад 2. Розв'язати диференціальне рівняння
y'-y*tan(x)=cos2(x).
Розв'язування: Візуальний аналіз правої частини показує, що вона не містить "y", тому це не рівняння Бернуллі, а лінійне ДР першого порядку.
Його розв'язок подаємо через добуток функцій, а далі розв'язуємо аналогічно методу Бернуллі.
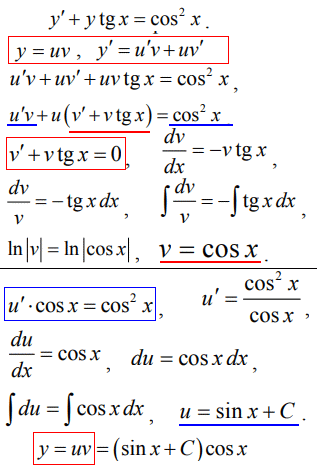
Це рівняння в цій публікації й для того, щоб Ви навчилися розрізняти яке ДР є рівнянням Бернуллі, а яке - ні. На практиці багато тестових завдань на класифікацію диф. р-нь, і Ви маєте знати чітко правила, щоб впевнено сказати - "Оце рівняння Бернуллі, це - рівняння схоже на ДР в повних похідних, а це зводиться до характеристичного р-ня.."
Тому і даємо Вам різноманіття умов, що Вас може чекати.
Приклад 3. Розв'язати диференціальне рівняння
y'-y/x=sin(2x)/x.
Розв'язування: Задане лінійне ДР першого порядку обчислюємо за методом Бернуллі.
Воно не є рівнянням Бернуллі, оскільки в правій частині немає "ігрика" в певному степені.
Основні перетворення ДР наведені в наступних формулах
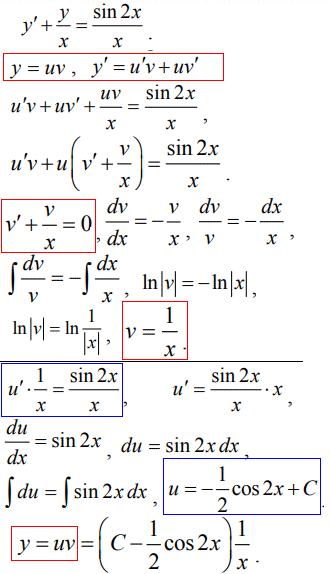
Тут v(x)=1/x при підстановці в друге ДР відносно u(x) спростить його до інтегрування синуса подвійного аргументу, що легко виконати на практиці. Якщо при обчисленнях у Вас виходять складні ДР, або самі розрахунки заходять в глухий кут, то слід перевірити попередні дії, адже, як правило, для вивчення теми підбирають ДР, які за допомогою наведеної заміни легко розділяти на два ДР, що інтегруються без проблем за допомогою табличних інтегралів.
Приклад 4. Обчислити диференціальне рівняння
y'-y/x=x*cos(x).
Розв'язування: ДР першого порядку розв'язуємо методом Бернуллі.
Уважно перегляньте хід розв'язування, щоб подібні приклади змогли так само легко розв'язати на практичних.
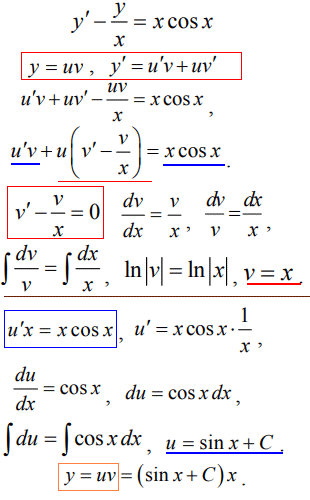
І запам'ятайте, що при розв'язуванні ДР рівняння в дужках при u (4 формула) сталу інтегрування слід покладати рівною нулю.
Бо проходить час, і деталі схеми Бернуллі поступово забуваються, а розв'язок такого р-ня заходить в тупик.
Стала C з першого рівняння деколи є цьому причиною.
Приклад 5. Розв'язати диференціальне рівняння
x2y'+5xy=-4.
Розв'язування: Обчислимо лінійне ДР першого порядку методом Ейлера-Бернуллі.
Запам'ятайте, що слід групувати множники при "u", та отримане ДР в дужках інтегрувати, покладаючи константу інтегрування рівною нулю C=0.
Буває, що про це забувають, і виникають труднощі при підстановці в друге ДР та визначенні "v(x)".
Спершу розділимо обидві частини рівняння на x2, а далі розпишемо за алгоритмом

Ну і наостанок, не забувайте записувати відповідь в такому вигляді, в якому її шукаємо - y(x)=u(x)*v(x), а то буває, що функції знайдені правильно, а перемножити їх і записати загальний розв'язок ДР забувають.
Не допускайте подібних помилок!
Приклад 6. Знайти розв'язок диференціального рівняння
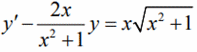
Розв'язування: Маємо лінійне ДР першого порядку, яке обчислюємо згідно з алгоритмом Бернуллі.
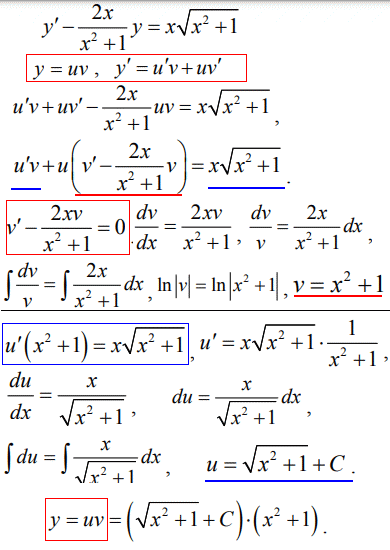
Чим більше Ви проведете подібних розділень ДР на два відносно шуканих функцій, тим легше Вам буде на практичних, тому лишень переглядом прикладів не обмежуйтеся. Обчислюйте, досліджуджуйте, що у Вас виходить добре, а що слід вивчити краще. І пам'ятайте, щоб добре розв'язувати ДР потрібні хороші знання з інтегрування, тому ці теми пов'язані і з допомогою наведених на сайті прикладів та інструкцій поступово маєте вивчити!


