Багато студентів запитують "Як знайти розв'язок диференціального рівняння?" Відповідь можливо неординарна, але що Ви знаєте про диференціальні рівняння, їх типи, поширені схеми обчислень? З цього потрібно починати. Сфери застосування диференціальних рівнянь були в загальному описані на попередньому уроці. Тут мова піде про один з найпростіших типів, в плані обчислень, серед можливих рівнянь, що Вас чекають. Почнемо з базових понять теорії, які Ви повинні знати і ми будемо виористоввати в термінології. Для одних це не потрібно, бо вони шукають готові відповіді з диференціальних рівнянь і думають, що в такий спосіб вирішать всі проблеми. Але це помилка, тому що не знання простих понять з теорії, це те саме що намагатися говорити, попередньо не вивчивши звуки та алфавіт.
Диференціальне рівняння першого порядку, які можна записати формулою
N(х)dx+М(у)dy=0 (1)
називають рівнянням з відокремленими змінними.
Їх не важко виявити серед інших рівнянь, основна ознака - коефіцієнти при dx та dy є функції (чи константи), які залежать лише від х при можнику dx та у при dy.
Щоб знайти загальний розв'язок (загальний інтеграл) рівняння з відокремленими змінними необхідно проінтегрувати рівняння (1)
Int(N(x), x) + Int(M(y),y) = С,
![]()
Для розуміння диференціальне рівняння (1) можна приймати, як умову рівності нулю повного диференціалу деякої функції двох змінних U(x,y)
![]()
Звідси слідує, що функція U(x,y)=С=const рівна сталій.
Диференціальне рівняння вигляду
f1(x)g1(y)dx+f2(x)g2(y)dy=0 (2)
називають диференціальним рівнянням з відокремлюваними змінними в симетричній формі.
В рівнянні (2) коефіцієнти при диференціалах dx та dy є добутками двох функцій: одна залежить тільки від x , а друга — від y . В області, де g1(y), f2(x) приймають відмінні від нуля значення рівняння з відокремлюваними змінними (2) зводиться до рівняння з відокремленими змінними
![]()
Звучить як гра слів: відокремленими, відокремлюваними, проте між ними як бачите є маленька різниця, і тепер Ви її знаєте.
Розглянемо типові для практики завдання на диф. рівняння, які в досить простий спосіб можна звести до рівнянь з відокремленими змінними.
Приклад 1 (1.9) Знайти загальний інтеграл диференціального рівняння
![]() Розв'язання: Маємо диференціальне рівняння першого порядку, за теорією його можна назвати рівняння з відокремлюваними змінними записане в диференціалах. Для його спрощення згрупуємо доданки, що містять dx, dy по різні сторони знаку рівності
Розв'язання: Маємо диференціальне рівняння першого порядку, за теорією його можна назвати рівняння з відокремлюваними змінними записане в диференціалах. Для його спрощення згрупуємо доданки, що містять dx, dy по різні сторони знаку рівності
![]()
Далі виділимо спільні множники для кожної суми та перепишемо рівняння у диференціалах до вигляду
![]()
Після цього все, що містить y переносимо до dy, те ж саме проробляємо з множниками , що містять змінну x. В результаті прийдемо до диференціального рівняння з відокремленими змінними
![]()
Тепер погляньте, чому дане рівняння називається з відокремленими змінними?- біля dx маємо функцію лише від "ікс", біля dy - лише від y.
Зінтегруємо диференціальне рівняння
![]()
Виносимо множнии, щоб при змінних в знаменниках стояли одиниці. Також, щоб в чисельнику отримати диференціали знаменника множимо обидві частини на 2
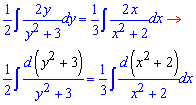
Це дозволяє спростити обчисення та після інтегрування отримати логарифми
![]()
Константу рекомендуємо внести під логарифм, для цього записуйте завжди її у вигляді C1=ln(C)
![]()
Щоб розкрити логарифми експонуємо (знаходимо експоненту) праву і ліву сторону рівняння
![]()
та виділяємо значення функції із отриманої залежності
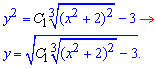
Кінцеве значення, що мітить подвійний корінь і є загальним інтегралом рівняння з відокремлюваними змінними.
Приклад 1*. Знайти частинний розв'язок диференціального рівняння (ДР) зі змінними, що розділяються.
y'=(2y-3)tg(x), y(2π)=6.
Обчислення: Запишемо рівняння в диференціалах, розділимо змінні та проінтегруємо диференціальне рівняння
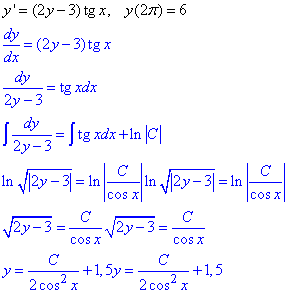
Остання формула є загальним розв'язком ДР.
Розв'яжемо задачу Коші, тобто підставимо початкову умову y(2π)=6 в загальний розв'язок ДР:
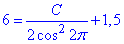 , звідси C=9.
, звідси C=9.
Остаточно, розв'язок задачі Коші:
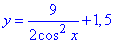 частинний розв'язок рівняння.
частинний розв'язок рівняння.
Приклад 2 (1.3) Знайти загальний інтеграл диференціального рівняння
![]() Розв'язання: Маємо рівняння в диференціалах першого порядку. Розділимо в рівнянні змінні, що містяться при dx, dy та перенесемо їх по різні сторони знаку рівності
Розв'язання: Маємо рівняння в диференціалах першого порядку. Розділимо в рівнянні змінні, що містяться при dx, dy та перенесемо їх по різні сторони знаку рівності
![]()
З перших дужок виносимо спільний для двох доданків множник y за дужки
![]()
Далі перегруповуємо множники так, щоб при dy отримати функцію лише від y, а при dx – функцію аргумента x. В результаті дістанемо диференціальне рівняння з відокремленими змінними
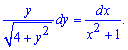
Після інтегрування

отримаємо кореневу залежність для y та арктангенс в результаті обчислення інтегралу від аргументу (права сторона).
![]()
Спробуємо записати розв'язок диференціального рівняння у вигляді залежності y(x). Для цього підносимо обидві частини до квадрату
![]()
та перенісши сталу в праву сторону, обчислюємо корінь квадратний
![]()
Це і є шуканий розв'язок диференціального рівняння.
Приклад 3 (1.15) Знайти загальний інтеграл диференціального рівняння
![]() Розв'язання: Дане рівняння необхідно звести під правило розв'язування рівнянь з відокремленими змінними. Для цього другий доданок, що зі знаком мінус, переносимо в праву сторону від знаку рівності
Розв'язання: Дане рівняння необхідно звести під правило розв'язування рівнянь з відокремленими змінними. Для цього другий доданок, що зі знаком мінус, переносимо в праву сторону від знаку рівності
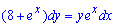
та розділяємо змінні
![]()
Далі інтегруємо праву та ліву сторону залежності
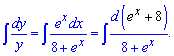
В результаті прийдемо до логарифмічного рівняння.
![]()
І знову нагоошуємо, що в такому вигляді як правило так не записують.
Доцільно, для компактності кінцевого розв'язку, сталу вносити під логарифм, тобто записувати
![]()
Потенціюючи (беручи експоненту) праву і ліву частину формули прийдемо до кінцевого вигяду розв'язку диференціального рівняння
![]()
Як Ви могли переконатися, приклади достатньо прості, методика обчислень диф. рівнянь легка для вивчення.
Приклад 4 (1.16) Знайти загальний інтеграл диференціального рівняння
![]() Розв'язання: Один з доданків (що не містить похідної ) переносимо за знак рівності
Розв'язання: Один з доданків (що не містить похідної ) переносимо за знак рівності
![]()
та записуємо рівняння в диференціалах.
![]()
Наступним кроком зводимо залежність до диференціального рівняння з відокремленими змінними.
Для заданого рівняння всього на всього перехресним діленням записуємо корені в знаменники
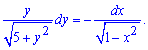
В такому вигляді можемо інтегрувати рівняння
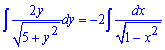
Ліва сторона, що містить функцію дасть в результаті кореневу залежність, при інтегруванні правої сторони за формулами отримаємо арксинус.
![]()
Виконуємо маніпуляції з коренем, щоб отримати залежність вигляду y=y(x)
![]()
Розв'язок диференціального рівняння матиме вигляд
![]()
На цьому ввідний урок завершено і основні висновки Ви повинні зробити самостійно.
Для закріплення теми рекомендуємо самостійно вирішити декілька із наступних завдань
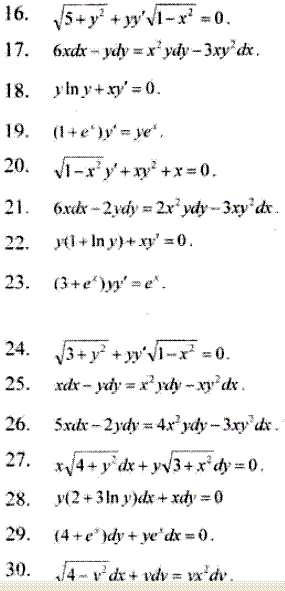
Хочете вірте, а хочете - ні, але це найпростіший тип диференціальних рівнянь, з яким Ви стикнетися на контрольній, екзаменах, практичних заняттях, модулях. Це можна сказати найважливіша частина, оскільки складні диференціальні рівняння доведеться спрощувати та зводити до рівнянь з відокремленими змінними.
Схему обчислень повинні завчити та знати на зубок - це один з основних методів розв'язування складних прикладів на диф. рівняння.


