Задача 16, 1.62 Колесо радіусом 10 см обертається так, що залежність лінійної швидкості точок, які лежать на ободі колеса, від часу задається рівнянням v=At+Bt2, де A=3 см/с2; B=1 см/с3.
Знайти кут між вектором повного прискорення і радіусом колеса в момент часу 4 с після початку руху.
Дано: |
| Розв’язання: Нехай |
Знайти: |
Оскільки кут є безрозмірною величиною (відносно фізичних величин), і вектор нормального прискорення 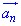 напрямлений вздовж радіуса колеса, то
напрямлений вздовж радіуса колеса, то  - кут між вектором повного прискорення
- кут між вектором повного прискорення 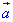 і вектором нормального прискорення
і вектором нормального прискорення 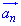 , тобто
, тобто 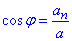 , або
, або 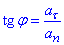 .
.
Для обертового руху колеса:
модуль вектора нормального прискорення знаходимо за формулою:
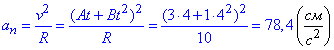
модуль вектора тангенціального прискорення рівний:
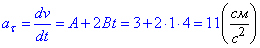
Обчислимо тангенс кута між векторами 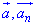 :
:
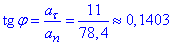
Далі через арктангенс знаходимо саме значення кута 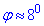 .
.
Відповідь: 8 градусів.
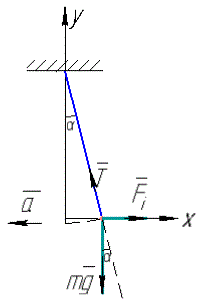
Задача 19, 2.22 До стелі трамвайного вагона підвішено на нитці кулю.
Швидкість вагона за час 3 с рівномірно зменшується від 18 км/год до 6 км/год.
В який бік і на який кут відхиляється за цих умов нитка з кулею.
Дано: |
| Розв'язання: |
Знайти: |
Під час руху трамвайного вагона на кульку буде діяти сила тяжіння 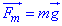 , яка напрямлена вертикально вниз;
, яка напрямлена вертикально вниз;
сила натягу нитки  , яка діє вздовж нитки;
, яка діє вздовж нитки;
сила інерції 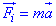 , яка діє протилежно до напрямку прискорення.
, яка діє протилежно до напрямку прискорення.
Закон рівноваги сил 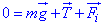 , або
, або 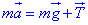 . (*)
. (*)
Вибираємо осі наступним чином:
вісь x горизонтально вправо (протилежно до прискорення вагона);
вісь y перпендикулярно до осі x (вертикально вгору).
Спроектуємо основне рівняння динаміки (*) на вибрані осі,
на вісь x:
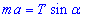 , звідси маємо формулу для натягу нитки
, звідси маємо формулу для натягу нитки
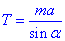
проекція на вісь y:
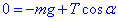 , звідси отримуємо рівняння
, звідси отримуємо рівняння
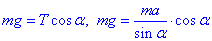 з якого можемо виразити тангенс шуканого кута
з якого можемо виразити тангенс шуканого кута
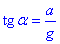 .
.
Знайдемо кут відхилення 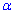 :
:
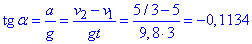
Отримаємо:
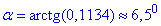
(знак мінус показує, що кулька відхиляється в протилежний до руху вагона бік).
Відповідь: 6,5 градуси.
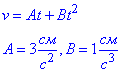 ,
,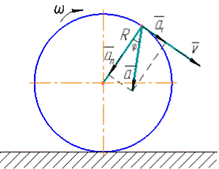
 - кут між вектором повного прискорення
- кут між вектором повного прискорення 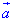 і радіусом К.
і радіусом К.
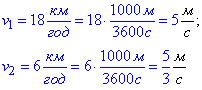
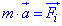 ,
,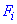 - рівнодійна всіх сил, що прикла-дена до підвішеної кулі.
- рівнодійна всіх сил, що прикла-дена до підвішеної кулі.
