Задача 17, 2.18 Струмінь води перетином 6 см2 вдаряється об стінку під кутом 600 до нормалі і пружно відбивається від стінки без втрати швидкості.
Знайти силу, яка діє на стінку, якщо відомо, що швидкість течії води в струмині 12 м/с.
Дано: | Розв’язання: Переведемо деякі величини в одиниці СІ: |
Знайти: |
За час 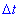 об стінку вдаряється маса води
об стінку вдаряється маса води 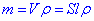 ,
,
де 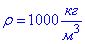 - густина води,
- густина води, 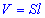 - об'єм води,
- об'єм води, 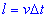 - довжина струменя води.
- довжина струменя води.
За законом збереження імпульсу маємо 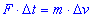 . (*)
. (*)
Нехай 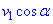 - швидкість з якою вода потрапляє на стінку (під кутом
- швидкість з якою вода потрапляє на стінку (під кутом 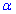 за умовою), тоді
за умовою), тоді 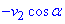 - швидкість, з якою вода відбивається від стінки, за умовою втрати швидкості немає, тому v=v1=v2.
- швидкість, з якою вода відбивається від стінки, за умовою втрати швидкості немає, тому v=v1=v2.
Звідси отримаємо приріст швидкості:
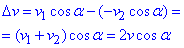
Отже, згідно (*) виражаємо силу, яка діє на стінку:
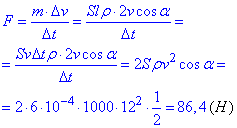
Відповідь: F=86,4 H.
Задача 18, 2.12 Тіло масою 0,5 кг рухається прямолінійно, при цьому залежність пройденого шляху від часу задається рівнянням s=A-Bt+Ct2-Dt3, де C=5 м/с2, D=1 м/с3.
Знайти силу, яка діє на тіло в кінці першої секунди руху.
Дано: 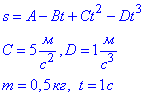 | Розв’язання: Згідно з ІІ законом Ньютона: |
Знайти: |
Задача 20, 2.30 Дві гирі масами 2 кг і 1 кг з'єднані ниткою , яка перекинута через невагомий блок.
Знайти:
1) прискорення, з яким рухаються гирі;
2) силу натягу нитки.
Тертям у блоці знехтувати.
Дано: |
| Розв’язання: |
Знайти: |
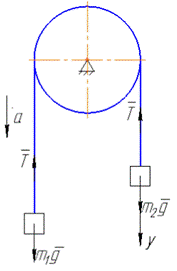
Вісь y направимо вертикально вниз вздовж дії сил тяжіння гирок і натягу нитки.
Очевидно, що гирка з більшою масою рухатиметься вниз, а гиря з меншою масою підніматиметься вгору.
Спроектуємо основне рівняння динаміки (*) на вісь y:
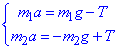
(додамо обидва рівняння),
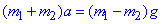
Отримаємо,
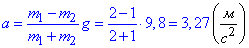 - прискорення, з яким рухаються гирі.
- прискорення, з яким рухаються гирі.
Із системи рівнянь знаходимо:
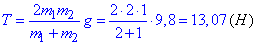 - силу натягу нитки.
- силу натягу нитки.
Відповідь: a=3,27 м/с2, T=13,07 Н.
При підготовці до практикуму з фізики, а саме відповідей до задач з механіки користувалися популярними довідниками та наступними книгами.
Використана література:
- Волькенштейн В. С. Сборник задач по общему курсу физики: Учебное пособие. - 11-е изд., перераб. - М.: Наука, Главная редакция физико-математической литературы, 1985. – 384 с.
- Кушнір Р. М. Загальна фізика. Механіка. Молекулярна фізика. Навч. посібн.– Львів: Видавничий центр ЛНУ ім. Івана Франка, 2003. – 404 с.
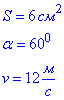
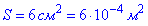 - площа поперечного перерізу струменя води.
- площа поперечного перерізу струменя води.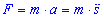 .
.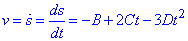 - швидкість тіла в момент часу
- швидкість тіла в момент часу 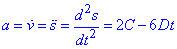 - прискорення тіла в момент часу
- прискорення тіла в момент часу 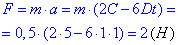
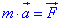 , (*)
, (*)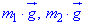 , і сили натягу нитки
, і сили натягу нитки 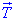 .
. 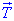 в усіх точках однакова;
в усіх точках однакова;
