Сьогодні на готових відповідях розберемо, як знаходити визначник матриці третього порядку.
Приклад 1. За правилом трикутника знайти визначники матриць
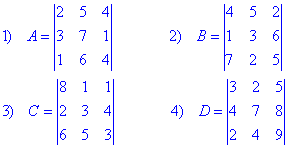
За формулою трикутників виконуємо обчислення визначників
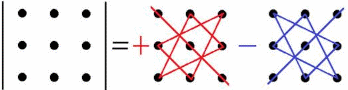
Почленно сумуємо добутки трьох елементів матриці за наведеною схемою. Її потрібно вивчити та .
1) Det(A)=2•7•4+5•1•1+4•3•6-(4•7•1+5•3•4+2•1•6)=56+5+72-28-60-12=33.
2) Det(B)=4•3•5+5•6•7+2•1•2-(2•3•7+5•1•5+4•6•2)=60+210+4-42-25-48=159.
3) Det(C)=8•3•3+1•4•6+1•2•5-(1•3•6+1•2•3+8•4•5)=72+24+10-18-6-160=-78.
4) Det(D)=3•7•9+2•8•2+5•4•4-(5•7•2+2•4•9+3•8•4)=189+32+80-70-72-96=63.
Приклад 2. Методом розкладу за рядком чи стовпцем знайти визначник матриці. Порівняти з результатом, отриманим за правилом трикутників. 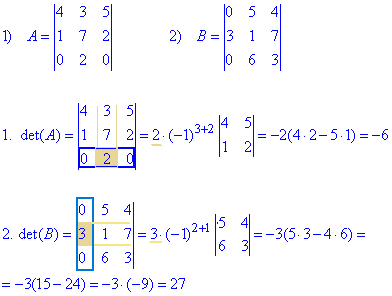
В першому прикладі другий елемент в третьому рядку=2 є ненульовим, тому розкладали визначник за 3 рядком. Нульові складові не враховували, а лише ті, що вносять вклад.
Другий визначник розкладемо за першим рядком, шукаємо мінор і помножуємо на (-1) в степені сум номера рядка та стовпця для ненульового елемента.
Далі знаходимо детермінант за відомою схемою трикутників.
Det(A)=4•7•0+3•2•0+5•1•2-(5•7•0+3•1•0+4•2•2)=0+0+10+0+0-16=-6.
Det(B)=0•1•3+5•7•0+4•3•6-(4•1•0+5•3•3+0•7•6)=0+0+72+0-45+0=27.
Як можна порівняти, багато добутків рівні нулю внаслідок двох нульових елементів, тому не дають вкладу.
Хоча їх доводиться записувати. Перший алгоритм швидший, але вимагає уваги при виписуванні визначника другого порядку та підрахунку степені j+k для множника (-1).
Приклад 3. Довести, що визначник матриці рівний нулю
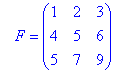
Бачимо, що усі елементи матриці ненульові, тому визначник третього порядку знаходимо за правилом трикутника
Δ=1•5•9+2•6•5+3•4•7-(3•5•5+2•4•9+1•6•7)=45+60+84-75-72-42=0.
Det(F)=0, що і потрібно було довести.
Приклад 4. Обчислити визначник матриці
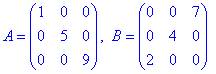
Задано дві діагональні матриці, в першій елементи головної діагоналі ненульові, в другої матриця ненульова бокова діагональ. Якщо не розкладати детермінант за елементами рядка чи стовпця, а пригадати правило трикутників, то при добутку елементів головної діагоналі стоїть знак «плюс», а при добутку елементів бокової діагоналі стоїть знак «мінус».
Тому визначники діагональних матриць рівні:
Δ1=1•5•9=45;
Δ2=-2•4•7=56.
Для перевірки вірності кінцевих відповідей обчисліть наведені визначники самостійно.
Приклад 5. Чому рівний визначник матриці
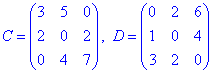
Перша матриця на боковій діагоналі має нульові елементи, всі решта ненульові.
В другої матриці на головній діагоналі всі елементи рівні нулю.
Обчислимо визначник матриці двома способами:
перший – за правилом трикутників,
другий – розкладом за рядком чи стовпцем.
Перший визначник рівний сумі добутку трьох елементів симетричних боковій діагоналі, тому входять зі знаком мінус.
Другий – рівний сумі добутку елементів навколо головної діагоналі, тому стоять зі знаком «плюс».
Це напряму слідує з правила трикутників.
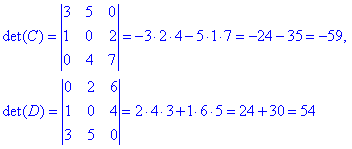
Далі обчислимо ці ж детермінанти шляхом розкладу першого Δ за елементами третього стовпця, другого Δ за елементами другого рядка. 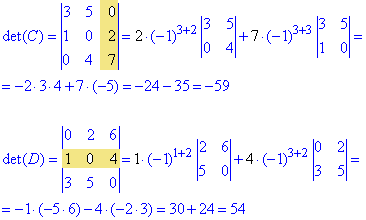
Щоб розібратися з останніми формулами почитайте правила розкриття визначників за елементами рядків та стовпців.
Далі Вас чекають нові завдання на визначники та обернені матриці. Переходьте та вивчайте алгоритми розрахунків.


