На попередніх уроках розглянули нерівності з коренями, які через ОДЗ, розкриття коренів та метод інтервалів розв'язали.
Тут розберемо складні в плані обчислень тестові завдання із ЗНО підготовки на ірраціональні нерівності.
Їх детальний аналіз багато Вас навчить нового, хоча ми мало віримо, що набереться з 10 студентів та абітурієнтів, які уважно дочитають відповіді до кінця.
Приклад 13.29 Розв'язати нерівність 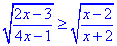
У відповідь записати добуток усіх цілих розв'язків нерівності.
Обчислення: Маємо дробову ірраціональну нерівність. Права сторона приймає менші значення, тому її підкореневий вираз провіряємо на те чи він приймає невід'ємні значення. Також підносимо нерівність до квадрату та замінюємо еквівалентною
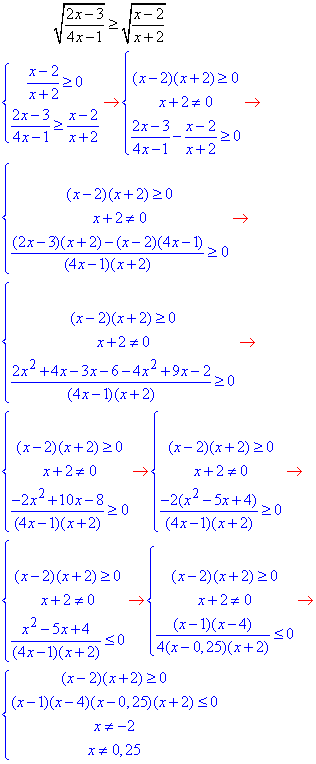
Зауважте, що при розкритті дробових нерівностей додатково слід виписувати умову, що знаменник не перетворюється в нуль.
На числову вісь наносимо точки – нулі функцій, в них функції в нерівностях змінюють знак.
Таким чином методом інтервалів встановлюємо розв'язки першої та другої нерівностей.

Множина спільних значень для двох нерівностей і буде розв'язком заданої нерівності x∈ [2; 4].
Числа 2; 3; 4 є цілими розв'язками заданої нерівності.
Знайдемо їх добуток: 2•3•4=24.
Відповідь: 24.
Приклад 13.31 Розв'язати нерівність 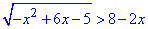
У відповідь записати добуток усіх цілих розв'язків нерівності.
Обчислення: В залежності від знаку виразу 8-2x змінюються і нерівності, які є рівносильні заданій.
Уважно перегляньте формулу нижче та дослідіть, чому саме такі нерівності ми виписали.
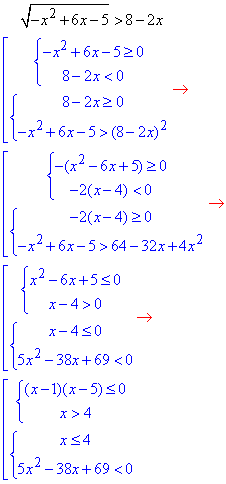
Знайдемо нулі функції через корені квадратного рівняння:
5x^2-38x+69=0,
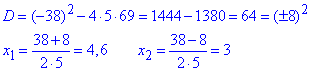
Записуємо кінцеву систему нерівностей, розклавши квадратичну нерівність на прості множники
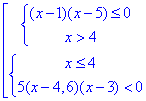
Далі методом інтервалів наносимо нулі функцій та заштриховуємо області де розв'язки першої та другої нерівності співпадають. Для складних ірраціональних рівнянь краще будувати стільки числових осей методом інтервалів, скільки систем нерівностей отримали.
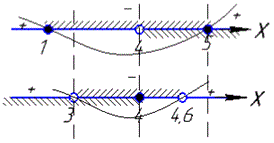 З першої системи отримали: x∈ [4; 5],
З першої системи отримали: x∈ [4; 5],
з другої системи отримали: x∈ (3; 4].
Суперпозиція розв'язків заданої нерівності (сукупність двох систем):
x∈ (3; 5].
Звідси слідує, що числа 4; 5 є цілими розв'язками заданої нерівності, 3 не входить.
Їх добуток: 4•5=20.
Відповідь: 20.
Приклад 13.35 Розв'язати нерівність 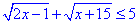 .
.
У відповідь записати суму найбільшого та найменшого розв'язків нерівності.
Обчислення: Перепишемо нерівність так, щоб в правій стороні отримати нуль
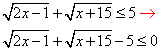
Запишемо функцію
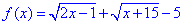
Знайдемо ОДЗ:
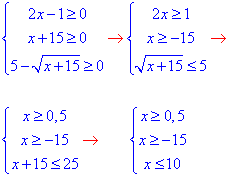
звідси 0,5≤x≤10.
Знайдемо нулі функції (f(x)=0), для цього рознесемо корені по різні сторони знаку нерівності та двічі піднесемо до квадрату:
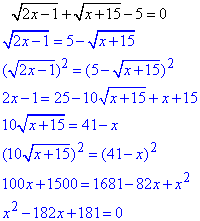
за теоремою Вієта знаходимо корені
x1=1 і x2=181 (не належить ОДЗ).
Нанесемо отримані значення на числову пряму
і знайдемо знак на кожному проміжку, враховуючи ОДЗ:

Оскільки нас цікавить f(x) ≤0, то запишемо розв'язки заданої нерівності:
x∈[0,5;1].
Звідси, xmin=0,5 найменший і xmax=1 найбільший розв'язки, їх сума:
xmin+xmax=1,5
Відповідь: 1,5.
Приклад 13.36 Розв'язати нерівність 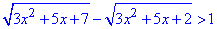
У відповідь записати суму всіх цілих розв'язків нерівності.
Обчислення: Перетворимо нерівність
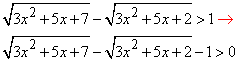
Запишемо функцію 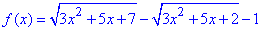
Знайдемо область визначення для коренів квадратних:
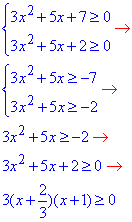
звідси x∈(-∞;-1]∪[-2/3; +∞).
Знайдемо нулі функції (f(x)=0):
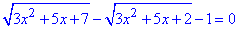
Бачимо, що доцільно виконати заміну змінних:
3x^2+5x+2=t, причому t≥0.
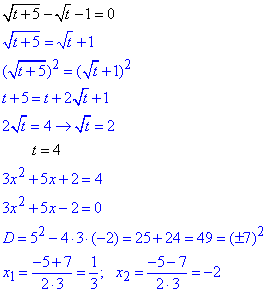
Після розв'язку параметричного рівняння повертаємося до заміни змінних та знаходимо нулі функції.
Нанесемо отримані точки на числову пряму та методом інтервалів знайдемо знаки на кожному проміжку, враховуючи ОДЗ:
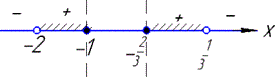 Оскільки f(x)>0, то розв'язками нерівності є два півінтервали:
Оскільки f(x)>0, то розв'язками нерівності є два півінтервали:
x∈(-2;-1]∪[-2/3; 1/3).
Звідси слідує, що числа -1; 0 є цілими розв'язками заданої нерівності.
Знайдемо їх суму:
-1+0=-1.
Відповідь: -1.
Приклад 13.38 Розв'язати нерівність 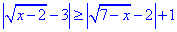
У відповідь записати добуток усіх цілих розв'язків нерівності.
Обчислення: Маємо складну нерівність з коренями та модулями.
Перетворимо початкову нерівність
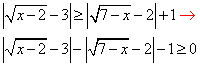
Запишемо функції 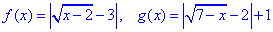
Знайдемо їх спільну ОДЗ:
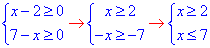
2≤x≤7, звідси x∈[2;7].
Побудуємо графіки функцій f(x) і g(x) на одній координатній площині на проміжку [2;7].
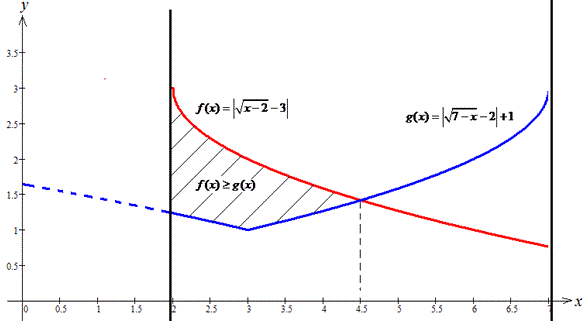
При побудові графіків мали:
x=3, звідси 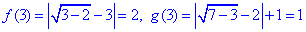
x=6, звідси 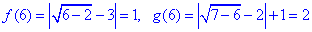
Отже, f(3)=g(6) і f(6)=g(3).
x=4, звідси 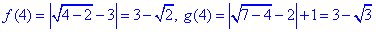
x=5, звідси 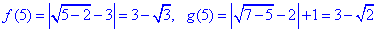
Отже, f(4)=g(5) і f(5)=g(4).
Легко помітити, що функції f(x) і g(x) мають симетричні значення відносно прямої x=4,5.
Обчислимо значення функцій f(x) і g(x) в точці x=4,5:
x=4,5, звідси 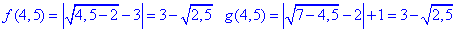
Отримали, що f(4,5)=g(4,5), звідси слідує, що рівняння f(x)-g(x)=0 має єдиний корінь, а саме x=4,5.
Оскільки f(x)≥g(x), то запишемо розв'язки заданої нерівності:
x∈[2;4,5].
Звідси слідує, що числа 2; 3; 4 є цілими розв'язками заданої нерівності.
Знайдемо їх добуток:
2•3•4=24
Відповідь: 24.
Приклад 13.39 Розв'язати нерівність 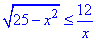
У відповідь записати добуток усіх цілих розв'язків нерівності.
Обчислення: Заміняємо нерівність рівносильною системою нерівностей, що не містить коренів та розв'язуємо її
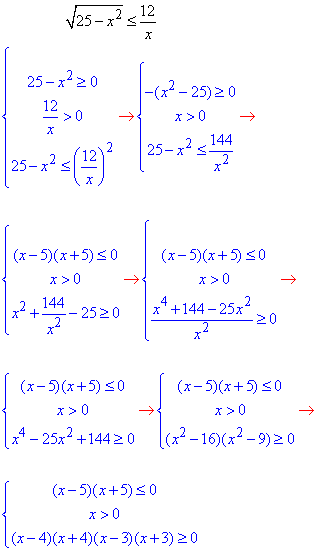
Методом інтервалів встановлюємо знаки між нулями другої та першої нерівностей.
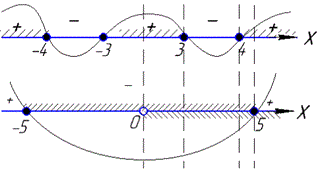 Перетином множин буде півінтервал (0;3] та проміжок [4; 5]
Перетином множин буде півінтервал (0;3] та проміжок [4; 5]
x∈(0;3]∪[4; 5].
Числа 1; 2; 3; 4; 5 є цілими розв'язками заданої нерівності.
Знайдемо їх добуток:
1•2•3•4•5=120
Відповідь: 120.
Приклад 13.40 Розв'язати нерівність 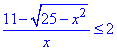
У відповідь записати модуль добутку всіх цілих розв'язків нерівності.
Обчислення: Перенесемо двійку в ліву сторону та зведемо до спільного знаменника
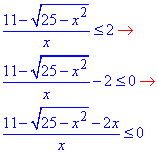
Дослідимо функцію
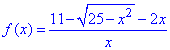
Знайдемо ОДЗ:
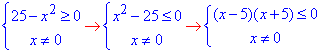
звідси x∈[-5;0)∪(0; 5].
Знайдемо нулі функції (f(x)=0):
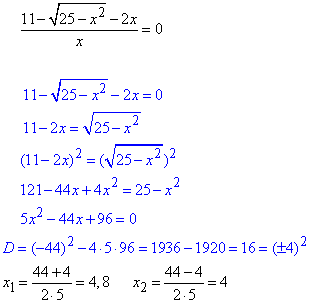
Нанесемо x1, x2 на числову пряму і знайдемо знак на кожному проміжку, враховуючи ОДЗ:
 Оскільки f(x)≤0, то розв'язками нерівності є два проміжки:
Оскільки f(x)≤0, то розв'язками нерівності є два проміжки:
x∈[-5;0)∪[4;4,8].
На множині розв'язків нерівності є значення -5; -4; -3; -2; -1; 4 є цілі числа.
Знайдемо їх модуль добутку:
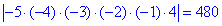
Відповідь: 480.
Приклад 13.41 Дано функції f(x)=x+1, 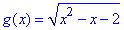 .
.
1) Розв'язати рівняння g(x)/f(x)=0;
2) розв'язати нерівність f(x)•g(x)≥0.
У відповідь записати найменший розв'язок нерівності.
Обчислення: 1) Розв'яжемо рівняння g(x)/f(x)=0, тобто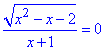
Встановимо ОДЗ нерівності:
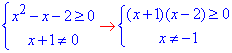
(Корені x1=-1 і x2=2 рівняння x^2-x-2=0 знайшли за теоремою Вієта)
Методом інтервалів знаходимо ОДЗ
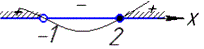 Отримали два півінтервали x∈(-∞;-1)∪[2;+ ∞).
Отримали два півінтервали x∈(-∞;-1)∪[2;+ ∞).
Залишилося прирівняти чисельник дробу до нуля
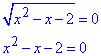
x1=-1 (не належить ОДЗ) і x2=2.
Звідси випливає, що x=2 - єдиний корінь рівняння g(x)/f(x)=0.
2) Розв'яжемо нерівність f(x)•g(x)≥0, тобто 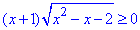
Складемо нерівності для рівносильної системи
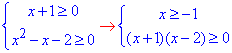
та методом інтервалів розв'яжемо їх.

Отримали сукупність точки та півінтервалу x∈{-1}∪[2;+ ∞).
Звідси слідує, що число -1 є найменшим розв'язком нерівності f(x)•g(x)≥0.
Відповідь: 1) 2; 2) -1.
На ЗНО тестах подібні завдання оцінюються найбільшою кількістю балів, хоча на їх обчислення потрібно немало часу, навіть якщо знати хід обчислень. Головне знайте, що подібного рівня знань можна досягти та для цього потрібно всього навсього практикувати самостійно і мати добрих наставників. Ми у свою чергу обіцяємо ділитися новими прикладами, які йдуть в ногу з вимогами ЗНО та ВУЗів та допоможуть Вам в навчанні.


