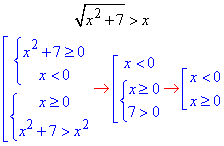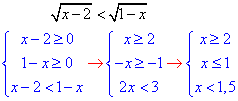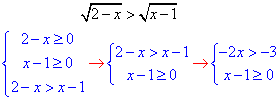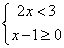Продовжуємо розв'язувати ірраціональні нерівності із ЗНО тестів. Ви навчитеся правильно виписувати ОДЗ, заміняти нерівності рівносильними системами та краще познайомитеся з методом інтервалів.
Приклад 13.22 Установити відповідність між заданими нерівностями (1–4) та рівносильними їм нерівностями або системами (А–Д).
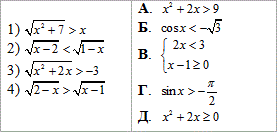Обчислення: Нерівності (або системи) називаються рівносильними, якщо множини їх розв'язків співпадають.
Для кожного пункту нервність замінюємо еквівалентною системою та через елементарні перетворення спрощуємо її.
| sin(x)>-Pi/2, |
Розв'язки нерівностей 1) і Г співпадають, тому вони рівносильні. 1 - Г
оскільки x≥2 і x≤1 одночасно, то задана нерівність розв'язків не має, тому x∈∅.. | cos(x)<- √3, ОДЗ: -1≤ cos (x) ≤1, оскільки - √3<-1, то задана нерівність розв'язків не має, тому x∈∅. |
Розв'язки нерівностей 2) і Б співпадають, тому вони рівносильні. 2 - Б.
√(2-x)> √(x-1), | x^2+2x≥0 |
Розв'язки нерівностей 3) і Д співпадають, тому вони рівносильні. 3 - Д.
|
|
Розв'язки нерівності 4) та системи В співпадають, тому вони рівносильні. 4 - В.
Приклад 13.23 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).
1) √x≥-4 | А. [-4;+∞) |
Обчислення: Проведемо швидкий аналіз нерівностей та встановимо множини їх розв'язків.
1) √x≥-4, x≥0,
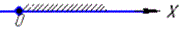тому x∈[0;+∞). 1 - В
2) √(x+4) ≥0, x+4≥0, x≥-4,
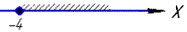звідси x∈[-4;+∞). 2 - А
3) √x≥2, {x≥0;x≥4}, x≥4,
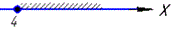отже x∈[4;+∞). 3 - Д
4) √(x-2) ≥0, x-2≥0, x≥2,
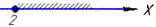отримаємо x∈[2;+∞). 4 - Г
Приклад 13.24 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).
1) √x≤2 | А. [-2;0] |
Обчислення: 1) √x≤2,
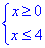
0≤x≤4,
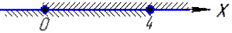тому x∈ [0;4]. 1 - В
2) √x≤-2, оскільки ОДЗ: √x≥0 і -2<0,
то задана нерівність розв'язків не має, тому x∈∅. 2 - Д
3) √(x-2) ≤2,
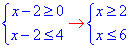
звідси 2≤x≤6,
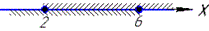тому x∈[2;6]. 3 - Г
4) √(x+2) ≤2,
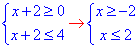
перетином множин є -2≤x≤2,
Наведемо їх на числовій осі
тому x∈ [-2;2]. 4 - Б
Приклад 13.25 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).
1) √(-x)≥-√3 | А. (-∞;-3] |
Обчислення: 1) √(-x)≥-√3, -x≥0, x≤0,
тому x∈ (-∞;0]. 1 - Б
2) √(-x)≤-√3, оскільки ОДЗ: √(-x) ≥0
а також -√3< 0, то задана нерівність розв'язків не має, тому x∈∅. 2 - Д
3) √(-x)≥√3,
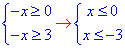
в підсумку x≤-3
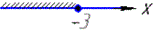отже x∈ (-∞;-3]. 3 - А
4) √(-x)≤√3,
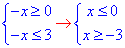
отримали проміжок -3≤x≤0,
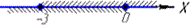x∈ [-3;0]. 4 - В.
Приклад 13.26 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).
1) √(x+2)>√x | А. ∅ |
Обчислення: 1) √(x+2)>√x
Виписуємо еквівалентну систему нерівностей
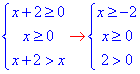
Звідси x≥0
отже [0;+∞). 1 - Г
2) √x >√(x-2)
Складаємо рівносильну систему нерівностей
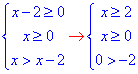
x≥2
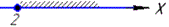тому розв'язки належать півінтервалу [2;+∞). 2 - Д
3) √(x+2)>√(-x)
Розкриваємо корені піднесенням до квадрату + умова на ОДЗ коренів
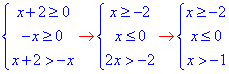
-1<x≤0
На осі чисел будуємо множину розв'язків
їх перетином є x∈ (-1;0]. 3 - В
4) √(-x) >√(x-2)
Розв'язуємо еквівалентну систему нерівностей
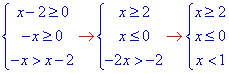
оскільки x≥2 і x<1 одночасно, то задана нерівність розв'язків не має, тому x∈∅. 4 - А
Приклад 13.27 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).
Обчислення: 1) √x≥x
Ірраціональне рівняння рівносильне системі нерівностей
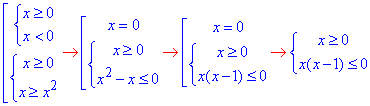
Уважно перегляньте формулу та розберіться чому саме так.
Знаки встановлюємо методом інтервалів, для цього будуємо числову вісь, наносимо нулі та виконуємо аналіз за відомим алгоритмом
Звідси випливає, що x∈[0;1]. 1 - В
2) √x≤x
Записуємо ОДЗ кореневої функції + розкриваємо ірраціональність
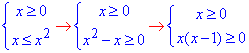
Методом інтервалів встановлюємо знаки
в підсумку розв'язком нерівності є точка та півінтервал x∈ [1; +∞)∪{0}. 2 - Г
3) √(-x)≥x
В залежності від знаку змінної ірраціональна нерівність буде еквівалентна системам нерівностей
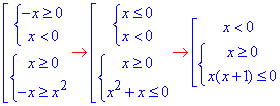
Далі методом інтервалів встановлюємо множину розв'язків
звідси x∈(-∞;0]. 3 - Б
4) √(-x)≤x
Оскільки зліва маємо корінь квадратний, то праву сторону теж слід обмежити, що приймала значення більш або рівні нулю.
На основі викладеного еквівалентна система нерівностей має вигляд
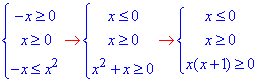
В перетині отримали одну точку x∈{0}. 4 - Д
Думаю, що приклади багатьом допомогли розібратися в ірраціональних нерівностях, Ви навчилися будувати рівносильні нерівності та методом інтервалів знаходити множини розв'язків. Далі підуть важчі завдання, але не менш цікаві в плані розрахунків.
