Продовжуємо аналізувати ірраціональні нерівності із ЗНО підготовки. Їх розв'язками є інтервали, півінтервали, проміжки, порожня множина, точки та їх поєднання. Всього маємо понад 40 готових прикладів, тож слідкуйте за номером та переходіть від простих завдань до складніших.
Як розкривати ірраціональні нерівності та оформляти відповіді Ви дізнаєтеся з наступних прикладів.
Приклад 13.14 Розв'язати нерівність 
Обчислення: Нерівність еквівалентна системі 3 нерівностей:
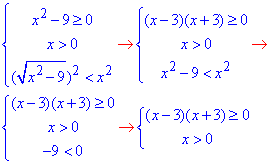
Перша в системі слідує з області визначення кореня квадратного.
Не забувайте, що якщо в одній стороні маємо корінь квадратний і він повинен приймати невід'ємні значення, то в іншій стороні вираз теж повинен бути невід'ємним. Тому тут виникає умова x>0.
Методом інтервалів встановлюємо знаки на інтервалах поза точками x=-3, x=3.
В підсумку, отримаємо x∈ [3;+∞).
Відповідь: [3;+∞). – В.
Приклад 13.15 Знайти множину розв'язків нерівності 
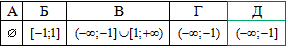Обчислення: Тут під коренем маємо квадратичну залежність яка для від'ємних "іксів" може приймати додатні значення. В таких випадках еквівалентну систему нерівностей розбивають на дві, коли права частина нерівності додатна, і коли від'ємна. Системи нерівностей об'єднують фігурними скобками, а от суперпозицію умов в залежності від знаку правої частини (x) квадратними скобками.
Після того наприкінці розрахунків множини розв'язків об'єднують.
На практиці це має наступний запис:
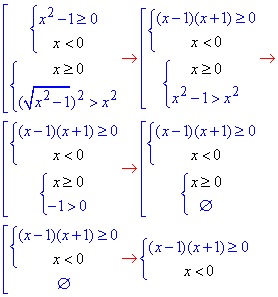
Уважно його проаналізуйте та запам'ятайте позначення, оскільки в подальших завданнях подібні еквівалентні системи нерівностей будуть часто зустрічатися.
Методом інтервалів будуємо розв'язки кінцевої системи нерівностей
та записуємо їх в інтервальній формі x∈ (-∞;-1].
Відповідь: (-∞;-1] – Д.
Приклад 13.16 Знайти множину розв'язків нерівності
√(3x+7)<x+1.
Обчислення: Записуємо ОДЗ кореневої функції + умову на праву частину + розкриття коренів піднесенням до квадрату
в еквівалентну систему:
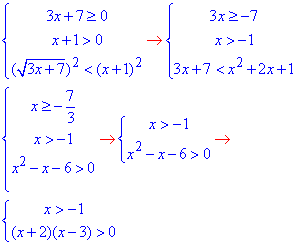
Після її розписання методом інтервалів будуємо
множину розв'язків нерівності x∈ (3;+∞).
Відповідь: x∈ (3;+∞) – В.
Приклад 13.17 Серед наведених нерівностей вказати ту, множина розв'язків якої містить множину натуральних чисел.
Обчислення: Маємо 5 варантів нерівностей, тому по черзі їх розв'язуємо, щоб встановити яка з них відповідає умові прикладу.
Для легкості читання пояснення перетворень тут зробимо мінімальними.
А. √x>1
звідси x∈ (1;+∞),
множина розв'язків заданої нерівності не містить множину натуральних чисел.
Б. √x>-1
x≥0, звідси x∈ [0;+∞),
множина розв'язків заданої нерівності містить множину натуральних чисел.
В. √x<-1
звідси x∈∅, розв'язків задана нерівність не має,
множина розв'язків заданої нерівності не містить множину натуральних чисел.
Г. √x<1
0≤x<1, звідси x∈ [0;1),
множина розв'язків заданої нерівності не містить множину натуральних чисел.
√(-x)<-1, -x≥0, x≤0, звідси x∈ (-∞;0],
множина розв'язків заданої нерівності містить множину натуральних чисел.
Відповідь: √x>-1 – Б.
Приклад 13.18 Серед наведених нерівностей вказати ту, множина розв'язків якої є відрізок [-2;0].
Обчислення: Розглянемо 5 простих нерівностей.
За порядком заміняємо кожну системою еквівалентних нерівностей та шляхом піднесення до квадрата розкриваємо корені квадратні.
А √(-x)≥ √2
x≤-2, звідси x∈ (-∞;-2].
Б. √x≥ √2,
x≥2, звідси x∈ [2;+∞).
В. √x≤√2
0≤x≤2, звідси x∈ [0;2].
Г. √(-x)≤√2
-2≤x≤0, звідси x∈ [-2;0].
множиною розв'язків заданої нерівності є проміжок [-2;0].
Д. √(-x)≤-√2
звідси x∈∅, розв'язків задана нерівність не має.
Відповідь: √(-x)≤√2 – Г.
Завдання тут нескладні, проте дають добру базу для обчислення складніших завдань.
Приклад 13.19 Розв'язати нерівність
Обчислення: Маємо добуток трьох коренів другого, третього, четвертого порядку відповідно.
Оскільки корені парних степеней приймають невід'ємні значення, а добуток всіх трьох коренів повинен бути меншим або рівним нулю, то лише корінь кубічний може давати від'ємні значення.
На основі викладених міркувань, складаємо еквівалентну систему нерівностей та обчислюємо її:
Результати, отримані вище, переносимо на числову вісь
В підсумку отримаємо x∈ [2;3]∪{5}.
Відповідь: [2;3]∪{5} – Д.
Приклад 13.20 Знайти суму цілих розв'язків нерівності
А | Б | В | Г | Д |
14 | 12 | 9 | 7 | 6 |
Обчислення: Тут один той самий вираз x-3 є одночасно під коренем квадратним та кубічним, тому при заміні еквівалентною системою нерівностей домінантною буде умова на ОДЗ кореня квадратного.
В результаті потрібно обчислити систему нерівностей:
На числовій осі множина коренів матиме вигляд
що рівносильно проміжку x∈ [3;5].
Задана нерівність має три цілих розв'язки, а саме 3; 4; 5.
Знайдемо їх суму:
3+4+5=12.
Відповідь: 12 – Б.
Приклад 13.21 Установити відповідність між заданими нерівностями (1–4) та множинами їх розв'язків (А–Д).
Обчислення: Розкриваємо корені квадратні піднесенням до квадрату. Крім того враховуємо умову на область визначення кореня квадратного.
1) 
задана нерівність виконується для будь-яких x, тому кажуть що розв'язками є множина дійсних чисел x∈R або x∈(-∞;+∞). 1 - А
2) 
Складаємо ОДЗ: √(x+1) ≥0 і -2< 0,
звідси слідує, що задана нерівність розв'язків не має, тому x∈∅. 2 - Г
3) 
або x<3
отже маємо x∈(-∞;3). 3 - В
4) 
наносимо розв'язки нерівностей на числову вісь
тому x∈ [1,5;3). 4 - Д
В такий спосіб розкривають корені та обчислюють прості ірраціональні нерівності. Попереду Вас чекають складні ірраціональні рівняння в яких множини розв'язків встановлюють методом суперпозиції різних умов, які у свою чергу дістають за рахунок знаку окремих виразів. Але про це піде мова в наступних уроках.
