Ірраціональні нервності починають розв'язувати в 10 класі школи і продовжують в 11 класі та на перших курсах у ВУЗах.
Нерівності розв'язують за наступною схемою:
1. Записують область визначення на всі функції, що містять нерівності, а саме:
- Вирази під коренями парних степенів повинні приймати невід'ємні значення.
- Якщо в одній частині нервності маємо лише корінь в парній степені, то вираз в іншій частині нерівності повинен приймати невід'ємні значення
- Знаменники дробових функцій не повинні перетворюватися в нуль
- врахування ОДЗ логарифмів, тригонометричних та інших функцій, що містяться в нерівності.
2. Знаходження нулів функцій та нанесення їх на множину розв'язків ОДЗ.
3. Далі методом інтервалів встановлення функції за межами знайдених нулів функцій.
Якщо задані складні нерівності то області визначення не розписують, а лише вкінці обчислень перевіряють правильність знайдених коренів (нулів) методом підстановки.
Як на практиці виглядає оформлення розв'язків Ви дізнаєтесь з наступних готових відповідей.
Це найкращий шлях запам'ятати теорію та навчитися застосовувати вивчене самостійно.
Приклад 13.1 Знайти множину розв'язків нерівності √x>-3.
Обчислення: Проаналізуємо нерівність √x>-3 .
Перше, що слід знати – це те, що корені парних степенів (1/2, 1/4,...) повинні приймати невід'ємні значення.
Це напряму слідує з області визначення кореневих функцій.
Запам'ятайте добре цю властивість.
Оскільки √x≥0, то задана нерівність еквівалентна нерівності x≥0.
Будуємо числову вісь, на ній відкладаємо точку 0 та заштриховуємо всі значення, що більші нуля.
Оскільки нерівність нестрога, то точка 0 входить в множину розв'язків і її на графіку замальовуємо.
В результаті отримаємо x∈[0;+∞).
Не забувайте, що плюс чи мінус безмежність досягнути не можна, тому в інтервальному записі позначаються круглими дужками.
Відповідь: x∈[0;+∞) – Г.
Приклад 13.2 Розв'язати нерівність √x≥5.
Обчислення: Нерівність розв'язуємо методом піднесення до квадрату.
Крім цього виписуємо область ОДЗ кореневої функції.
В результаті √x≥5 еквівалентна системі нерівностей:
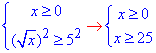
Будуємо числову вісь, наносимо на неї знайдені точки та множини розв'язків.
Всі значення, що задовільнятимуть одночасно обидві нерівності і будуть шуканими розв'язками x∈[25;+∞).
Відповідь: [25;+∞) – В.
Приклад 13.3 Розв'язати нерівність √x ≤4.
Обчислення: Задана нерівність рівносильна системі двох нерівностей:
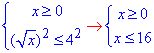
Перша з них слідує з ОДЗ кореневої функції, друга є результатом розкриття кореня квадратного.
На рисунку наведені знайдені точки та заштриховані множини розв'язків.
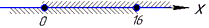Суперпозиція обох множин і буде розв'язком нерівності x∈[0;16].
Відповідь: [0;16] – Д.
Приклад 13.4 Знайти множину розв'язків нерівності √x<-2.
Обчислення: Оскільки √x≥0, то задана нерівність не має розв'язків,
тобто x∈∅.
Хто не розуміє чому так, подумайте чи може корінь квадратний бути від'ємним на множині дійсних чисел.
Відповідь: ∅– Б.
Приклад 13.5 Розв'язати нерівність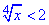 
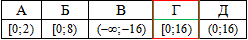
Обчислення: Маємо корінь четвертого порядку.
Ірраціональну нерівність замінюємо еквівалентною системою нерівностей, де зразу для розкриття кореня підносимо вираз до четвертого степеня:
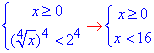
Будуємо числову вісь із знайденими множинами коренів
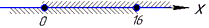Спільним для двох нерівностей є півінтервал x∈[0;16).
Відповідь: [0;16) – Г.
Приклад 13.6 Розв'язати нерівність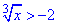 
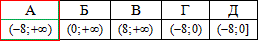Обчислення: Тут вперше маємо корінь непарного степеня, а саме кубічний.
Для коренів непарних степеней областю визначення є вся дійсна вісь, тому при розкритті таких коренів ніяких додаткових нерівностей не виникає.
Тому просто підносимо нерівність до кубу
звідси x>-8.
Оскільки нерівність строга, то точка x=-8 на числовій осі буде "виколена" (або незамальована), а саме значення не входить в множину розв'язків нерівності та в інтервальному записі позначається круглою дужкою.
Остаточно отримаємо x∈(-8;+∞).
Відповідь: (-8;+∞) – А.
Приклад 13.7 Знайти множину розв'язків нерівності
√(x+3)> √(x-1).
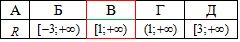Обчислення: Тут маємо два корені квадратні по обидві сторони знаку "більше".
Виписуємо еквівалентну систему трьох нерівностей та обчислюємо її:
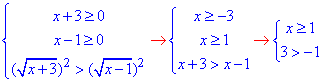
Наносимо знайдену точку на числову вісь та заштриховуємо множину розв'язків нерівності
звідси x≥1 або в інтервальному записі
x∈[1;+∞), що відповідає варіанту В ЗНО тестів.
Відповідь: [1;+∞) – В.
Приклад 13.8 Розв'язати нерівність √x≤x.
Обчислення: Записуємо обмеження на область визначення кореневої функції та піднесенням до квадрату позбуваємося кореня:
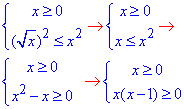
Точки наносимо на числову вісь, далі встановлюємо знаки на інтервалах та заштриховуємо області.
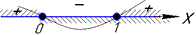З графіка та обчислень записуємо розв'язки нерівності x∈{0}∪ [1;+∞).
Відповідь: {0}∪ [1;+∞) – Д.
Приклад 13.9 Скільки цілих розв'язків має нерівність √(2x) ≥x?
Обчислення: Думаю, вам не варто нагадувати, що цілими числами є -5, -4, ...,0, 1, 2, 3 і т. д.
Задану нерівність розкриваємо піднесенням до квадрата + умова на значення підкореневої функції:
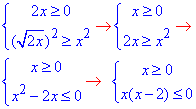
Методом інтервалів знаходимо проміжок, де одночасно виконуються обидві нерівності
Звідси слідує, що розв'язки повинні належати проміжку x∈[0;2].
Виписуємо цілі значення 0; 1; 2 та їх кількість.
Відповідь: три – Г.
Приклад 13.10 Розв'язати нерівність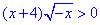 
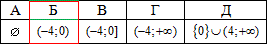
Обчислення: ОДЗ кореня квадратного + обмеження на множник дають рівносильну систему нерівностей:
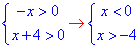
Множини розв'язків обох нерівностей намалюємо на числовій осі
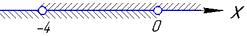Оскільки нерівність строга, то крайні точки не є розв'язками нерівності, тому в інтервальному записі x∈(-4;0) їх позначаємо круглими дужками.
Відповідь: (-4;0) – Б.
Приклад 13.11 Скільки цілих розв'язків має нерівність (5-x) √x>0?
Обчислення: Заміняємо нерівність рівносильною системою та обчислюємо:
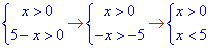
Будуємо числову вісь та знайдені множини коренів нерівностей
Їх спільним перетином є інтервал x∈(0;5).
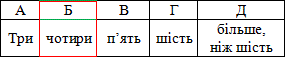
Задана нерівність має чотири цілих розв'язки, а саме 1; 2; 3; 4.
Відповідь: чотири – Б.
Приклад 13.12 Розв'язати нерівність (x-6) √x≥0.
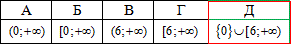Обчислення: По аналогії з попередніми завданнями, нерівність заміняємо еквівалентною системою:
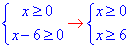
Будуємо графік
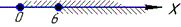Спільними є точка та півінтервал x∈{0}∪ [6;+∞).
Відповідь: {0}∪ [6;+∞) – Д.
Приклад 13.13 Розв'язати нерівність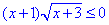 
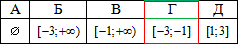Обчислення: Нерівність заміняємо еквівалентною системою нерівностей:
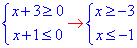
Після їх розписання наносимо розв'язки на числову вісь
Записуємо розв'язок нерівності x∈[-3;-1].
Відповідь: [-3;-1] – Г.
Попереду ще біля 30 прикладів із ЗНО підготовки на ірраціональні нерівності. Завдання будуть складніші, тож перед ознайомленням з ними добре розберіть готові відповіді.
