Сьогодні розглянемо складні ірраціональні рівняння, які необхідно розв'язувати за допомогою заміни змінних.
Які саме бувають заміни змінних, та як при цьому спрощують розрахунки Ви дізнаєтесь з наступних прикладів.
Приклад 12.37 Розв'язати рівняння
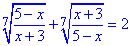Обчислення: Маємо корені 7 порядку, непарного степеня, тому під ними вирази можуть бути від'ємними. Обмеження слід накласти на знаменники дробів, вони не повинні бути рівні нулю.
Звідси отримуємо дві нерівності для області визначення:
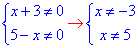
Далі, з аналізу рівняння бачимо що дроби під коренями обернено пропорційні.
Тому доцільно зробити заміну змінних:
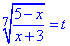
тоді
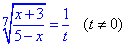
Початкове рівняння зводимо до наступного
t+1/t=2,
t2+1=2t,
t2-2t+1=0,
(t-1)2=0,
t-1=0,
t=1.
Повертаємося до заміни
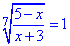
та розв'язуємо
,
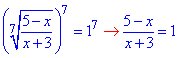5-x=x+3,
x+x=5-3,
2x=2,
x=1.
Відповідь: 1.
Приклад 12.38 Розв'язати рівняння
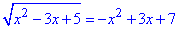У відповідь записати модуль різниці коренів.
Обчислення: Підкоренева функція повинна приймати більші або рівні нулю значення. Таке саме обмеження слід накласти і на праву сторону рівняння. Звідси дістанемо систему двох нерівностей для ОДЗ:
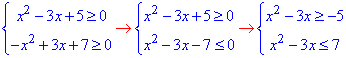
В підсумку змінні повинні належати проміжку
-5≤x2-3x≤7.
З аналізу самого рівняння бачимо що слід робити заміну змінних.
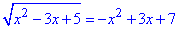
За нову змінну можна вибрати як весь підкореневий вираз t=x2-3x+5 (оскільки в правій частині можемо зробити такий доданок) так і його частину x2-3x=t. Від цього результат не поміняється, тільки швидкість обчислень.
Ви спробуйте перший варіант заміни змінних самостійно і вкінці переконайтеся що отримаєте ідентичний розв'язок, коли за заміну змінних вибрати x2-3x=t.
Отримане при цьому рівняння підносимо до квадрату та розписуємо
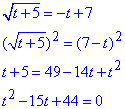
За теоремою Вієта знаходимо корені:
t1=-11, t2=4
Повертаємося до заміни змінних
x2-3x=t
1. x2-3x=-11<-5,
тому корені рівняння не належать ОДЗ.
2. x2-3x=4,
x2-3x-4=0,
За формулою Вієта знаходимо розв'язки квадратного рівняння:
x1=-1 і x2=4.
Обидва корені належать ОДЗ, оскільки належать інтервалу -5<4<7.
Знайдемо модуль різниці коренів:
|x1-x2|=|-1-4|=|-5|=5.
Відповідь: 5.
Приклад 12.39 Знайти суму коренів рівняння
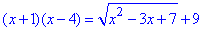Обчислення: Записуємо нерівності для визначення ОДЗ:
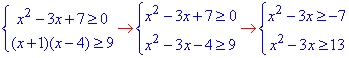
звідси головною є x2-3x≥13.
Розписуємо рівняння
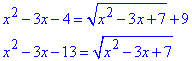
За заміну змінних можна вибрати вираз: x2-3x=t,
в результат отримаємо
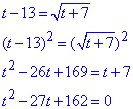
Квадратне рівняння обчислюємо за теоремою Вієта:
t1=9 і t2=18.
Повертаємося до заміни змінних
x2-3x=t
1. x2-3x=9<13,
тому корені рівняння не належать ОДЗ.
2. x2-3x=18
x2-3x-18=0,
За теоремою Вієта маємо:
x1=-3 і x2=6.
Корені другого рівняння x2-3x=18>13 належать ОДЗ.
За умовою обчислимо суму закоренів x1 і x2:
x1+x2=-3+6=3.
Відповідь: 3.
Приклад 12.40 Розв'язати рівняння
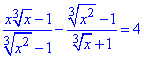Обчислення: Корінь кубічний може приймати від'ємні значення, але знаменник не повинен дорівнювати нулю.
Звідси маємо систему двох рівнянь для області визначення:
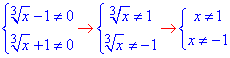
Внесемо під корінь кубічний змінну в чисельнику першого дробу.
Далі за формулою різниці квадратів розпишемо деякі частини дробів та спростимо рівняння.
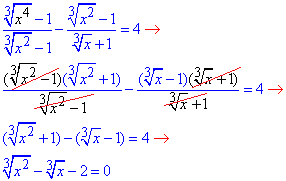
З аналізу останнього р-ня слідує, що потрібно зробити заміну змінних:
та перейти до обчислень квадратного рівняння
t2-t-2=0,
t1=-1 і t2=2.
Повернемося до заміни та розкриємо кубічні корені:
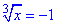(не задовольняє ОДЗ);
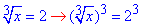
x=8.
Відповідь: 8.
Приклад 12.43 Розв'язати рівняння
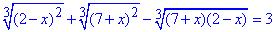У відповідь записати суму коренів.
Обчислення: За формулами скороченого множення маємо неповну суму кубів, тому для її отримання слід помножити та поділити всі три корені на певний множник. Після цього знаменник переносимо в праву сторону та піднесенням до кубу понижуємо корені
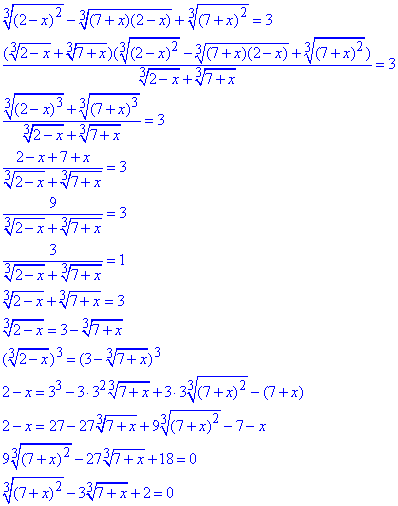
Бачимо, що тут корінь кубічний слід позначити новою змінною:
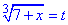, тоді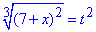 
Для квадратного рівняння t2-3t+2=0 за теоремою Вієта отримаємо t1=1 і t2=2.
Повертаємося до заміни змінних і знаходимо розв'язки
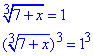
7+x=1, x1=-6.
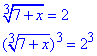
7+x=8, x2=1.
Знайдемо суму коренів заданого рівняння:
x1+x2=-6+1=-5.
Відповідь: -5.
Приклад 12.44 Розв'язати рівняння
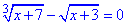Обчислення: Під коренем кубічним функція може приймати і від'ємні значення, а от корінь квадратний цього не допускає.
Звідси маємо нерівність для ОДЗ: x+3≥0, або x≥-3.
Щоб розкрити ірраціональність піднесемо обидві частини до 6 степеня та розпишемо.
Чому підносили до 6, тому що найменше спільне кратне НСК(2,3)=6, і це найменший степінь який розкриє одночасно обидва корені.
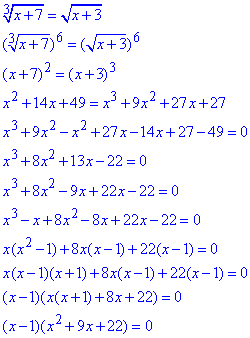
x-1=0, x=1.
Квадратне рівняння дійсних коренів немає, тому що дискримінант менший нуля.
x2+9x+22=0,
D=92-4•1•22=81-88=-7<0.
Отже, x=1 - єдиний корінь заданого рівняння.
Відповідь: 1.
Приклад 12.45 Розв'язати рівняння
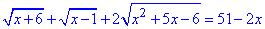
Обчислення:Складне ірраціональне рівняння починаємо розв'язувати з встановлення області визначення:
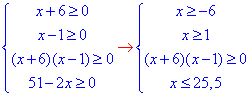
звідси 1≤x≤25,5, або x∈[1;25,5].
Далі квадратний тричлен під коренем розкладаємо на множники (x+6)(x-1), а саме рівняння за формулами скороченого множення доповнюємо, щоб отримати суму коренів у квадраті
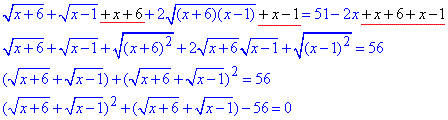
Робимо заміну змінних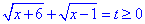 
та зводимо до квадратного рівняння
t2+t-56=0,
за теоремою Вієта t1=-8<0 (не задовольняє), t2=7.
Повертаємося до заміни змінних і, двічі піднісши до квадрату, розкриваємо корені
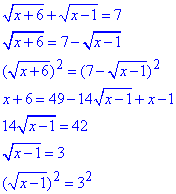
x-1=9, x=10.
Відповідь: 10.
На цьому прикладі добре видно, що потрібно робити, щоб для складного ірраціонального рівняння швидко знайти розв'язки та які схеми ефективно застосовувати.
Приклад 12.46 Розв'язати рівняння
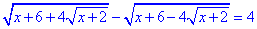
У відповідь записати найменший корінь.
Обчислення: Маємо вложені корені, тому їх краще буде звести під суму або різницю у квадраті.
Але спере виписуємо нерівності для ОДЗ:
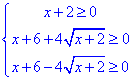
Оскільки в системі присутні ірраціональні нерівності на обчислення яких потратимо багато часу, то її розв'язувати не будемо, лише вкінці перевіримо, чи задовольняють ОДЗ знайдені корені початкового рівняння. Це оптимальний шлях при складних рівняннях.
Під коренями виділяємо квадрати виразів, далі корені квадратні розкриваємо через модулі підкореневих виразів
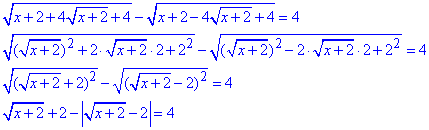
Тут перший доданок і без модуля більший нуля, тому знак модуля не писали.
1. Щоб розкрити модуль у випадку коли вираз в ньому додатний отримаємо
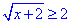
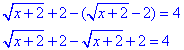
Отримали тотожність 4=4.
Перевіримо чи при цьому існують корені квадратні з (x+2)
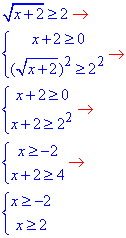
звідси x≥2.
2. Далі розкриваємо модуль, коли підмодульна функція приймає від'ємні значення
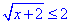
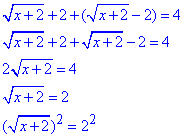
x+2=4, x=2.
В підсумку робимо висновок, що коренями заданого рівняння є всі числа, які не менше 2, тобто x≥2.
(перевіркою встановлюємо, що всі вони задовольняють ОДЗ).
x=2 найменший корінь заданого рівняння.
Відповідь: 2.
Приклад 12.47 Розв'язати рівняння
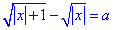У відповідь записати найбільше значення параметра a, за якого рівняння має корені.
Обчислення: Для довільного x, очевидно, що 
, тому, звідси a>0.
Це дуже важливий висновок, адже він суттєво звужує область пошуку потрібного параметра.
При розв'язуванні ірраціональних рівнянь уважно аналізуйте, що Вам задано та під яку схему слід зводити розрахунки.
Один корінь переносимо в праву сторону та, піднесенням до квадрату, спрощуємо рівняння
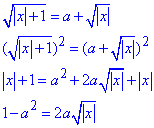
Оскільки a>0 і |x|≥0, то задане рівняння має корені, якщо виконується система нерівностей
параметр лежить в інтервалі 0<a≤ 1.
Таким чином, при 0<a≤1 задане рівняння має корені;
a=1 - найбільше значення, при якому задане рівняння має корені.
Відповідь: 1.
На цьому поки що всі приклади із ЗНО підготовки з теми ірраціональні рівняння, далі підуть ірраціональні нерівності.
Вчіть схеми, що тут наведені і більше розв'язуйте самостійно!
