Раціональні рівняння - квадратні, модульні, лінійні

Останні 11 прикладів з теми передбачають обчислення квадратних рівнянь з модулем, модульних та лінійних рівнянь.
Пояснення не важкі і будуть корисними усім школярам, що готуються до вступу у ВУЗи.

Ви можете безкоштовно завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).

Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж

Зміст: В посібнику наведені поради та схеми правильного обчислення завдань, базові формули та означення та подібні до тестових завдання.
Усі задачі однієї теми розміщені в порядку зростання складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.

Тема 8. Цілі раціональні рівняння

Приклад 8.24 Скільки коренів має рівняння x^2-7|x|+10=0?

Обчислення: Маємо поєднання квадратного рівняння з модульним.
В залежності від знаку "ікс" під модулем, після його розкриття отримаємо два подібні квадратні р-ня, обчислення яких наведено в таблиці

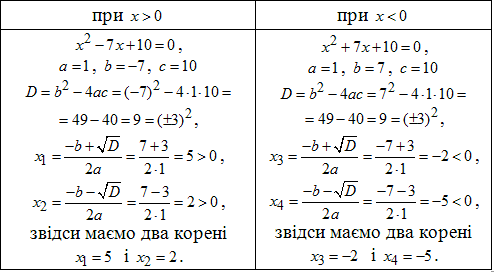
Очевидно, що "ікс" не дорівнює нулю.
Оскільки всі корені задовольнили умові відкриття модуля, то їх є 4.
Відповідь: чотири – Г.

Приклад 8.25 Установити відповідність між рівняннями (1–4) та їх коренями (А – Д).

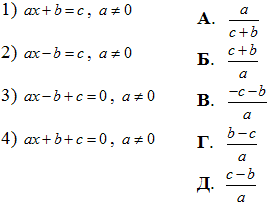
Обчислення: Задоно прості лінійні рівняння з буквеними коефіцієнтами.
В залежності від умови їх розв'язками будуть наступні дроби.
1) ax+b=c, ax=c-b, звідси x=(c-b)/a - Д;
2) ax-b=c, ax=c+b, тоді x=(c+b)/a - Б;
3) ax-b+c=0, ax=b-c, звідси x=(b-c)/a) - Г;
4) ax+b+c=0, ax=-c-b, тоді x=(-c-b)/a - В.
Оскільки виконували ділення на а, то необхідно, щоб його значення не дорівнювало нулеві.

Приклад 8.26 Установити відповідність між рівняннями (1–4) та кількістю їх розв'язків (А – Д).

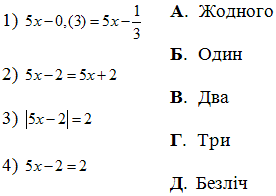
Обчислення: Періодичні числа перетворюємо до дробів, в третьому пункті розкриваємо рівняння з модулем.
Відповіді порівнюємо з тестовими.
1) 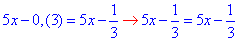, звідси 0=0 - безліч коренів - Д;
2) 5x-2=5x+2, 5x-5x=2+2, звідси - жодного кореня - А;
3) |5x-2|=2;
При додатній підмодульній функції знак в дужках залишаємо без змін
5x-2=2; 5x=4; x=0,8.
При від'ємній (5x-2<0) змінюємо знак правої частини на від'ємний
5x-2=-2; 5x=0; x=0 звідси x1=0 і x2=0,8 - два корені - В;
4) 5x-2=2, 5x=4, звідси x=0,8 - один корінь - Б.

Приклад 8.27 Установити відповідність між рівняннями (1–4) та їх коренями (А – Д).

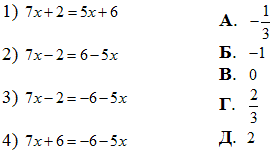
Обчислення: Наведені в умові приклади не що інше, як порівняння лінійних рівнянь.
Тому зводимо їх до лінійних та знаходимо "ікс".
1) 7x+2=5x+6;
7x-5x=6-2;
2x=4, звідси x=4/2=2 - Д;

2) 7x-2=6-5x;
7x+5x=6+2;
12x=8, звідси x=2/3 - Г;

3) 7x-2=-6-5x;
7x+5x=-6+2;
12x=-4, звідси x=-1/3 - А;

4) 7x+6=-6-5x;
7x+5x=-6-6;
12x=-12, звідси x=1. - Б.

Приклад 8.28 Установити відповідність між рівняннями (1–4) та їх коренями (А – Д).

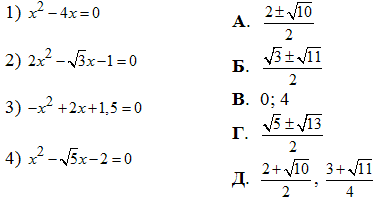
Обчислення: Знаходимо корені квадратних та неповних квадратних рівнянь та перевіряємо з відповідями до тесту.
1) x:^2-4x=0, x(x-4)=0, звідси x1=0 і x2=4 - В;

2) 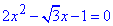тут a=2, b=-√3, c=-1, тому
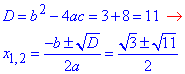звідси - Б;

3) -x^2+2x+1,5=0, тут a=-1, b=2, c=1,5,
знаходимо дискримінант та корені р-ня
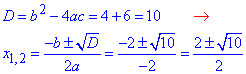, звідси - А;

4) 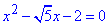, тут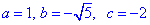
корені визначаємо через дискримінант р-ня
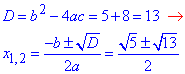, звідси - Г.

Приклад 8.29 Установити відповідність між рівняннями (1–4) та множинами їх коренів (А – Д).

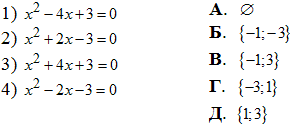
Обчислення: Встановимо корені рівняння за теоремою Вієта, оскільки квадратні рівняння зведені:
1) x^2-4x+3=0, звідси x1=1 і x2=3, отримали {1;3} - Д;

2) x^2+2x-3=0, звідси x1=-3 і x2=1, отримали {-3;1} - Г;

3) x^2+4x+3=0, звідси x1=-3 і x2=-1, отримали {-1;-3} - Б;

4) x^2-2x-3=0, звідси x1=-1 і x2=3, отримали {-1;3} - В.

Приклад 8.30 Установити відповідність між рівняннями (1–4) та їх коренями (А – Д).

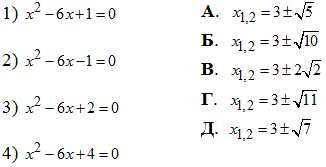
Обчислення: Тут всюди маємо зведені квадратні рівняння, які, в залежності від дискримінанта, можуть мати один, два або жодного кореня.
Хід обчислень та результати наведено далі.
1) x^2-6x+1=0, коефіцієнти при квадратичній формі a=1, b=-6, c=1.
Виконуємо розрахунки

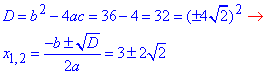
Корені відповідають пункту - В;

2) x^2-6x-1=0, тут a=1, b=-6, c=-1,
обчислюємо дискримінант і розв'язки

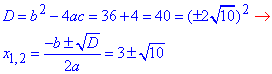
звідси - Б;

3) x^2-6x+2=0, тут a=1, b=-6, c=2, тому

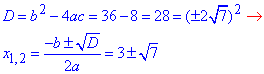
відповідь - Д;
4) x^2-6x+4=0, тут a=1, b=-6, c=4, тому

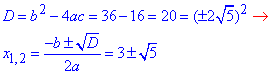
серед відповідей - А.

Приклад 8.31 Установити відповідність між виразами (1–4) та їх значеннями (А – Д), якщо x1 та x2 – корені квадратного рівняння x^2-5x-4=0.
1) x1•x2+x1+x2 ;
2) x1^2+x2^2 ;
3) (x1+x2)^2+2x1•x2 ;
4) x1^2x2+x1x2^2 ;
А. -20;
Б. 1 ;
В. 33;
Г. 65;
Д. 17;

Обчислення: Оскільки задане квадратне рівняння зведене (біля x^2 стоїть коефіцієнт 1), то за теоремою Вієта маємо:
x1+x2=5, а x1•x2=-4
1) x1•x2+x1+x2=-4+5=1 - Б;

2) Розпишемо квадрат суми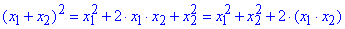

Підставляємо відомі значення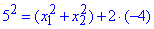

та спрощуємо

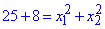
В результаті отримаємо x1^2+x2^2=33 - В;

3) Аналогічні перетворення виконуємо для пунктів 3), 4)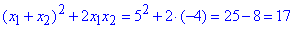
- Д;

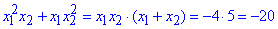4) - А.

Приклад 8.32 Установити відповідність між рівняннями (1–4) та кількістю їх коренів (А – Д).
1) x^4-13x^2+36=0;
2) x^4-5x^2-36=0;
3) x^4+13x^2+36=0;
4) x^5+5x^3-36x=0;
А. Жодного;
Б. Один;
В. Два;
Г. Три;
Д. Чотири.
Обчислення: В умовах задані біквадратні рівняння, які розв'язуємо шляхо заміни змінних x^2=t.
1) x^4-13x^2+36=0, нехай x^2=t>0, тоді t^2-13t+36=0 за теоремою Вієта t1=4 і t2=9.
Повертаємося до заміни
x^2=4 і x^2=9, тому x1=2; x2=-2 і x3=3; x4=-3 - чотири корені - Д;

2) x^4-5x^2-36=0, нехай x^2=t>0, тоді t^2-5t-36=0 за теоремою Вієта t1=-4<0 (не задов.) і t2=9.
Розписуємо x^2=9, тому x1=3; x2=-3 - два корені - В;

3) x^4+13x^2+36=0 нехай x^2=t>0, тоді t^2+13t+36=0 за теоремою Вієта t1=-4<0 і t2=-9<0 (обидва корені не задов.)
Тобто 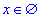- жодного кореня - А;

4) x^5+5x^3-36x=0;
x(x^4+5x^2-36)=0,
x1=0; нехай x^2=t>0, тоді
t^2+5t-36=0
за теоремою Вієта t1=4 і t2=-9<0 (не задов.)
Тобто x^2=9, тому x2=3; x3=-3, а також x1=0 - три корені - Г.

Приклад 8.33 Установити відповідність між рівняннями (1–4) та множинами їх коренів (А – Д).

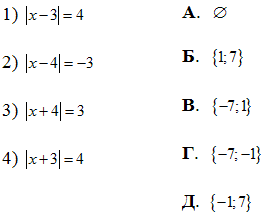
Обчислення:
1) |x-3|=4, звідси x-3=4, x1=7; x-3=-4, x2=-1, маємо {-1;7} - Д;

2) |x-4|=-3, (у модуля величина додатна), тому x= порожній множині - А;

3) |x+4|=3, звідси x+4=3, x1=-1; x+4=-3, x2=-7, маємо {-7;-1} - Г;

4) |x+3|=4, звідси x+3=4, x1=1; x+3=-4, x2=-7, маємо {-7;1} - В.

Приклад 8.34 Установити відповідність між рівняннями (1–4) та множинами їх коренів (А – Д).

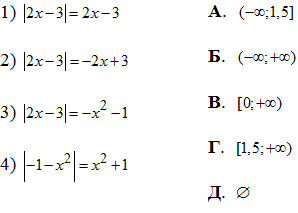
Обчислення:
1) |2x-3|=2x-3, звідси :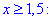
2x-3=2x-3, 0=0,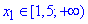
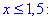-2x+3=2x-3, 4x=6, x2=1,5, маємо 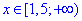- Г;

2) |2x-3|=-2x+3, звідси
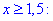2x-3=-2x+3, 4x=6, x1=1,5;
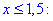-2x+3=-2x+3, 0=0, маємо 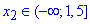- А;

3) |2x-3|=-x^2-1, звідси

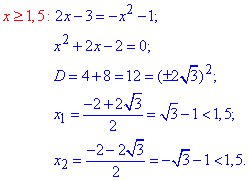
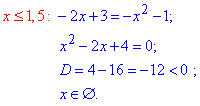
маємо - Д;

4) Винесемо знак під модулем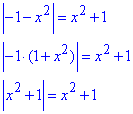

звідси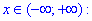
x^2+1=x^2+1, маємо 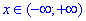- Б.

Приклад 8.35 Розв'язати рівняння

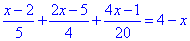
Обчислення: Зводимо дроби до спільного знаменника, далі сумуємо доданки, що отримали в чисельнику та групуємо ті, що містять "ікс" та вільний член.
Вкінці залишається обчислити просте лінійне рівняння, яке під силу розв'язати кожному школяру.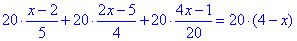

4(x-2)+5(2x-5)+(4x-1)=20(4x-1);
4x-8+10x-25+4x-1=80-20x,
4x+10x+4x+20x=80+8+25+1,
38x=114,
x=114/38, x=3.
Відповідь: 3.