Як спростити дробові вирази?

Завдання на дроби взяті із Посібника для підготовки до зовнішнього незалежного тестування з математики
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж

Завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).

Зміст: В довіднику наведені поради щодо проходження ЗНО з математики та взірці тестових завдань, основні формули та правила для проходження кожної схеми.
Задачі подано в порядку зростання складності із ростом номера.
Абсолютно всі бажаючі можуть безкоштовно долучитися до ЗНО підготовки та пройти ряд тем, з якими маєте труднощі на практичних.
Пояснення всюди мінімалістичні та містять тільки найнеобхіднішу інформацію, левова частка міститься в формулах.
Їх просимо уважно проаналізувати та поставити себе на наше місце.
Чи правильний на Вашу думку хід обчислень?
Чи зрозумілі для Вас відповіді до прикладів на дроби?
Прочитайте до кінця і Ви знатимете, як правильно спростити дріб.

Тема 4. Дробово-раціональні вирази

Базові означення, які пояснюють що таке дробово-раціональні вирази та раціональні дроби наведено далі.

Знання означень мало в чому Вам допоможе на практичних, тестах, екзаменах.
Тому перш ніж приступати до розрахунків освіжіть в пам'яті базові правила, які допомагають швидко спростити дробові вирази.

Основні властивості дробу:

Перейдемо до аналізу готових відповідей, та послідовно розберемо 30 відповідей до завдань на дроби.
Початкову умову, якщо вона буде громіздка, наводити не будемо, лише на початку обґрунтування розрахунків.

Приклад 4.1 Знайти суму дробів 8/(5a-2)+3/(2-5a)

Обислення: В другому доданку виносимо мінус в знаменнику та зводимо до єдиного дробу

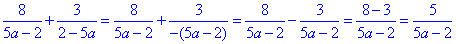
Просте завдання, яке під силу виконати кожному.
Виникає питання: що складного в завданнях на дроби?
Про це Ви дізнаєтесь дочитавши цю і наступну за нею статті до кінця.
Відповідь: 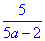– Г.

Приклад 4.2 Обчислити різницю дробів

Обчислення: В першому дробі знаменник подамо на основі формули різниці квадратів.
Далі зводимо дроби до спільного знаменника та після обчислення різниці спрощуємо до вигляду, наведеного в одному з результатів тестів.

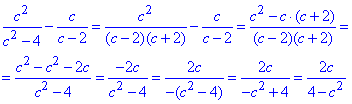
Відповідь: 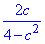– А.

Приклад 4.3 Обчислити добуток дробів

Обчислення: Всюди де міститься формула різниці квадратів виконуємо розклад на два множники, а наступним кроком спрощуємо спільні множники чисельника та знаменника дробу
.
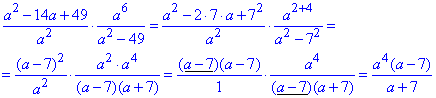Відповідь: 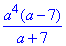– В.

Приклад 4.4 Знайти частку дробів

Обчислення: Ділення дробів замінюємо множенням на обернений вираз, а далі застосовуємо загальні формули спрощення дробових виразів.

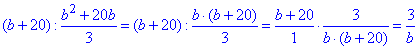
В результаті отримали компактний результат.
Відповідь: 3/b – Г.

Приклад 4.5 Обчислити значення дробового виразу

Обчислення: Спершу знаходимо добуток дробів, це не важко.
Далі дроби зводимо до спільного знаменника та через різницю знаходимо чисельник дробу.

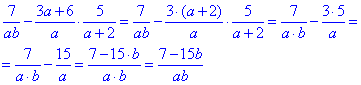
Відповідь: 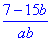– Б.

Приклад 4.6 Знайти частку виразів

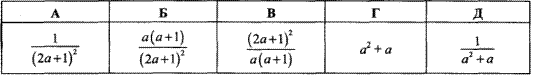
Обчислення: Спершу в першій дужці виконуємо сумування дробів.
Наступним кроком ділення на 2a+1 замінюємо множенням на обернений вираз та спрощуємо в чисельнику та знаменнику однакові вирази.

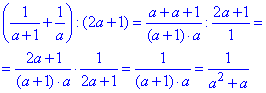
Відповідь: 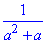– Д.

Приклад 4.7 Знайти суму

Обчислення: Зводимо все під спільний знаменник та сумуємо дроби

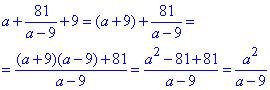
Відповідь: 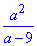– Б.

Приклад 4.8 Спростити дробові вирази

Обчислення: Схема незмінна від умови до умови.
Тут краще спростити добуток дробів, а далі обчислити суму простих дробів.

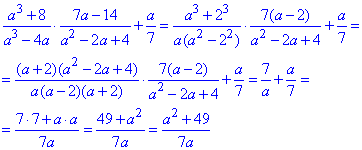
Відповідь: 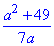– Г.

Приклад 4.9 Обчислити частку дробів

Обчислення: Спершу за правилами для показникових функцій розписуємо другу дужку.
Далі знаходимо частку, замінивши ділення множенням на обернене значення

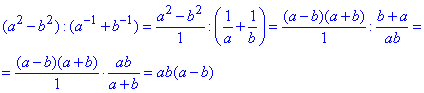
Відповідь: ab(a-b) – А.

Приклад 4.10 Спростити дріб

Обчислення: Застосовуючи більшість властивостей дробів та показників, спрощуємо дріб

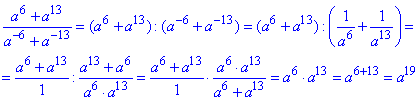
Відповідь: a^19 – Г.

Приклад 4.11 Знайти добуток

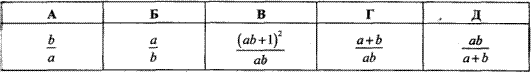
Обчислення: В другій дужці доданки зводимо до єдиного дробу, підносимо його до мінус першого степеня, а далі множення на перший дріб.

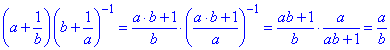
Відповідь: a/b – Б.

Приклад 4.12 Якщо 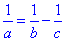, то с=?

Обчислення: Відомі перенесемо по одну сторону знаку рівності, а невідомі по другу.
Далі знаходимо обернений дріб

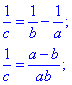
В результаті отримаємо

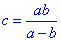
Відповідь: – Г.

Приклад 4.13 Відомо, що (a+b)/b=4. Знати значення виразу b/a.

Обчислення: Переходи тут не важкі, тому розбирайте формули самостійно

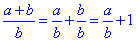
звідси a/b+1=4, тобто a/b=3 і b/a=1/3.
Відповідь: b/a=1/3 – Г.

Приклад 4.14 Відомо, що 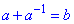. Знайти значення виразу .

Обчислення: Підносимо суму до квадрату та виділяємо вираз, який потрібно знайти

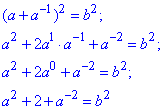
Відповідь: 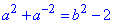– В.

Приклад 4.15 Якщ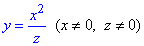о , то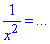

Обчислення: Перетворення зводяться до знаходження оберненого дробу

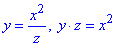
або 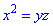, звідси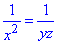

Відповідь: Д.

Приклад 4.16 Спростити вираз

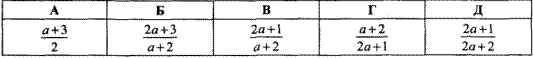
Обчислення: Спершу сумуємо дроби в знаменнику, а далі перетворивши 2 дріб отримаємо

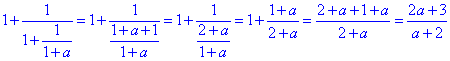
Запам'ятайте правило з оберненням дробу, він важливий в розрахунках та часто зустрічається.
Відповідь: 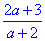– Б.