Правила розкриття логарифмічних нерівностей

Сьогодні на готових відповідях до ЗНО тестів будемо вчитися основним технікам розкриття логарифмічних нерівностей.
Під "розкриттям" тут і надалі маємо на увазі зведення (перетворення) логарифмічних нерівностей до простих (таких, що не містять логарифма).
Алгоритм обчислень:
1. Виписати ОДЗ логарифмів та усіх функцій;
2. Звести нерівність до логарифмів з однією основою;
3. Розкрити нерівність: 
якщо основи рівні вирази в логарифмах прирівнюємо, зберігаючи знак нерівності, якщо основа логарифма більша за одиницю або
змінюємо знак нерівності на протилежний, якщо основа менша одиниці.
Перегляньте уважно приклад та запам'ятайте, коли знак нерівності зберігаємо, а коли міняємо не протилежний при розкритті логарифмічної нерівності?

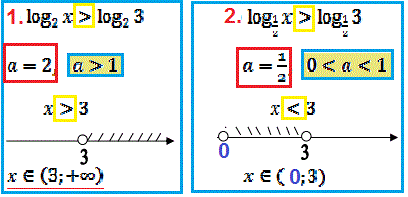
Основні формули розкриття логарифмічних нерівностей

Усі логарифмічні нерівності, які Вам доведеться розв'язувати, можна замінити еквівалентними за допомогою формул переходу:

Перейдемо до практики, всього підготовлено 50+ прикладів із Збірника для ЗНО підготовки під ред. Капіносова за 2010р. завдань. Якщо в якийсь момент Вам буде важко розбирати формули переходу, тоді повертайтеся до попередніх двох уроків, в яких є відповіді прості приклади на логарифмічні нерівності з програми для 10-11 класів.

Приклади розкриття нерівностей з логарифмом

Приклад 17.4 Розв'язати нерівність
log_0,1(2x-1)≥log_0,110-log_0,12.

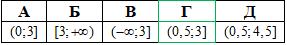
Розв'язування: Застосовуємо властивість, що різниця логарифмів рівна логарифму частки
log_a(b)+log_a(c)=log(b•c)
перетворимо праву частину

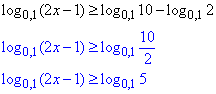
Основа менша одиниці 0,1<1, тому знак нерівності змінимо на протилежний.
З урахуванням ОДЗ логарифма (в І нерівності системи), отримаємо

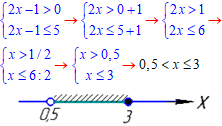
Розв'язок x∈(0,5;3].
Відповідь: (0,5;3] – Г.

Приклад 17.5 Знайти множину розв’язків нерівності
log(sin1)>2log(sin(7))

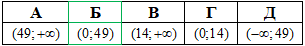
Розв'язування: Внесемо множник під логарифм за правилом c•log_ab=log_ab^c

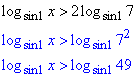
Основа менша одиниці sin(1)<1, тому знак при опусканні логарифмів змінимо на протилежний.
Випишемо ОДЗ логарифма x>0 + розкриття нерівності з логарифмом
{x>0, x<49}⇔ 0<x<49.
Будуємо множину розв'язків на числовій осі

та записуємо інтервалом x∈(0;49).
Відповідь: (0;49) – Б.

Приклад 17.6 Знайти множину розв’язків нерівності
log₅x<2.

Розв'язування: Скористаємося властивістю – логарифм основи рівний одиниці
log_aa=1

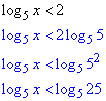
Основа більша одиниці 5>1, тому знак залишимо без змін.
З врахуванням ОДЗ, отримаємо
{x>0,x<25}⇔ 0<x<2549.
Розв'язок нерівності

x∈(0;25).
Відповідь: (0;25) – В.

Приклад 17.10 Розв'язати нерівність
(1/5)^log_1/5(2-x)<2.

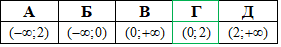
Розв'язування: Спростимо показниковий вираз за формулою основної логарифмічної тотожності
a^log_ab=b:

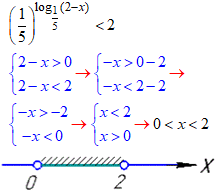
Перша умова 2-x>0 є врахування ОДЗ логарифма, про неї не забувайте.
Розв'язок x∈(0;2).
Відповідь: x∈(0;2) – Г.

Приклад 17.16 Знайти множину розв'язків нерівності
log_x5<1.

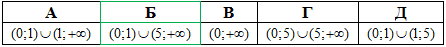
Розв'язування: Логарифм основи рівний =1, це що до способу перетворення правої сторони
log_x5<1,
log_x5<log_xx.
Нерівність еквівалентна двом системам нерівностей:

Отримали множини розв'язків
0<x<1 і x>5

Інтервальний запис x∈(0;1)∪(5;+∞).
Відповідь: (0;1)∪(5;+∞) – Б.

Приклад 17.20 Розв'язати нерівність x^x<1, якщо x>0, застосувавши логарифмування.

Розв'язування: Уважно перегляньте та запам'ятайте метод логарифмування:
x^x<1,
lg(x^x)<lg(1)
Оскільки основа десяткового логарифма 10>1 , то при логарифмуванні знак нерівності не змінився.
x•lg(x)<0.
ОДЗ: x>0.
Застосуємо метод інтервалів, розв'яжемо відповідне рівняння:
x•lg(x)=0, тобто lg(x)=0, або x=0.
x₁=1, x₂=0.
Отримані корені відкладемо на числовій осі та визначимо знаки на інтервалах.
Розв'язки нерівності:

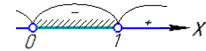
x∈(0;1).
Відповідь: (0;1) – В.

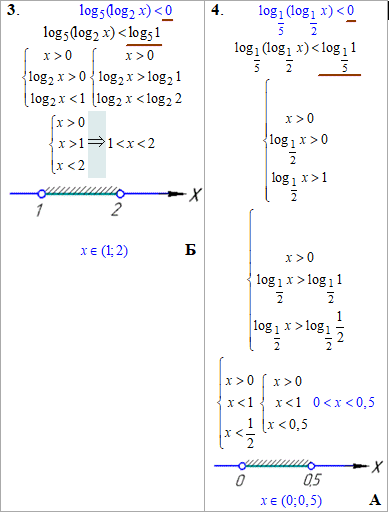
Приклад 17.28 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).

Розв'язування: Права сторона нерівностей з логарифмом рівна нулю, тому тут слід застосувати властивість логарифма:
log_a1=0.
Схеми зведення до простих нерівностей наведені в таблиці.

Приклад 17.11 Скільки цілих розв'язків має нерівність -2<log_1/2x<3?

Розв'язування: Маємо двосторонню нерівність з логарифмом, замінюємо її системою еквівалентних нерівностей та зводимо до однієї основи

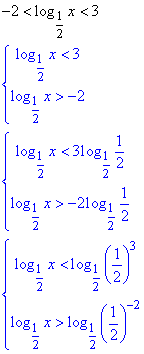
Складаємо систему нерівностей:
1. Враховуємо ОДЗ x>0.
2. Розкриваємо логарифмічні нерівності пам'ятаючи, що слід змінити знак на протилежний, оскільки основа менша одиниці 1/2<1.

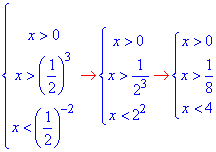
Сумарно маємо 1/8<x<4,

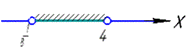
звідси x∈(1/8;4).
Випишемо усі цілі розв'язки:
1; 2; 3.
Їх кількість =3.
Відповідь: три – В.

Приклад 17.31 Розв'язати нерівність
lg(x)+6log^x10≤5.
У відповідь записати кількість цілих розв'язків нерівності.
Розв'язування: За формулою переходу до іншої основи

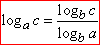
в другому логарифмі міняємо x з 10-кою місцями, далі сумуємо доданки та переходимо до квадратної нерівності від логарифмів:

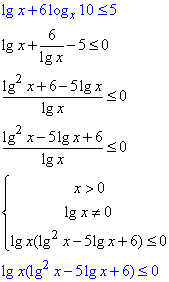
заміна lg(x)=t, де t≠0,
t(t²-5·t+6)≤0.
Застосовуємо метод інтервалів для розкриття нерівності
t²-5·t+6=0.
за теоремою Вієта:
t¹=2, t²=3.
На числову вісь наносимо точки та, шляхом підстановки, з'ясовуємо знаки нерівності на проміжках від мінус нескінченності до плюс

t∈(-∞;0)∪[2;3].
Не забуваємо про заміну та повертаємося до логарифмів:

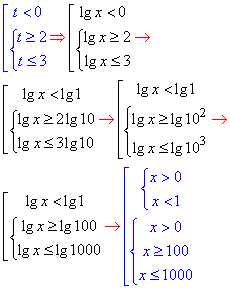
0<x<1; 100≤x≤1000.

Розв'язком є два інтервали x∈(0;1)∪[100;1000].
Від тисячі перших додатних чисел віднімемо перші 99, які не є розв'язками нерівності:
1000-99=901– кількість цілих значень.
Відповідь: 901.

Ви тільки що розглянули нерівності звідні до простих, далі підуть логарифмічні нерівності звідні до квадратних, з модулями, та складні приклади із ЗНО тестів.