Логарифмічні нерівності. Приклади 10-11 клас

Для розв'язування логарифмічних нерівностей Ви повинні добре знати властивості логарифма.
Функція y=log_ax монотонно зростає, якщо основа логарифма більша одиниці a>1, та спадає на ОДЗ (x>0), якщо основа менша одиниці 0<a<1. Перегляньте графік, при основі a>1 більшому значенню аргументу (x) відповідає більше значення логарифма, для  y=log_ax з основою меншою одиниці (0<a<1) навпаки – чим менше значення "ікс" тим більше значення приймає логарифм.

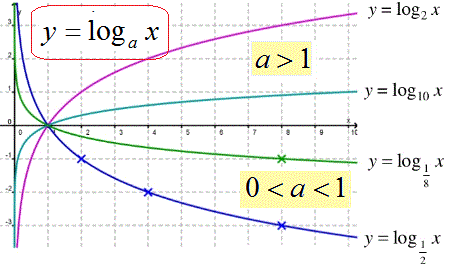
Тому при розкритті логарифмічних нерівностей ( log_ax>b) знак нерівності зберігаємо (x>a^b) якщо a>1, та змінюємо на протилежний (x<a^b), якщо основа менша одиниці 0<a<1.
Це правило вивчіть та не забувайте!

Приклад 1. Розкрити нерівність log₂(x-3)>5.
Обчислення: ОДЗ логарифма:
x-3>0;
x>3.
Перейдемо до простої нерівності, основа 2>1, тому знак залишаємо
x-3>2⁵;
x>32-3=29.
Розв'язок x∈(29;+∞).
Відповідь: (29;+∞).

Приклад 2. Знайти множину розв'язків log_0.5(x-5)<√4.
Обчислення: ОДЗ логарифма:
x-5>0;
x>5.
Основа 0,5<1, тому при спрощенні нерівності міняємо знак на протилежний
x-5>0,5^√4;
x>0,5²+5=0,25+5=5,25.
Розв'язок x∈(5,25;+∞).
Відповідь: (5,25;+∞).

Приклад 3. Скільки цілих коренів має нерівність log₅(x+4)<-1.
Обчислення: ОДЗ логарифма:
x+4>0;
x>-4.
Основа 5>1, тому знак нерівності зберігаємо.
Формулу переходу до простої нерівності можна вивести, якщо скористатися властивістю, що логарифм основи рівний одиниці:
log₅(x+4)<-1·log₅5;
log₅(x+4)<log₅5^-1.
Опускаємо логарифми і порівнюємо вирази
x+4<5^-1;
x<0,2-4=-3,8.
З врахуванням ОДЗ, розв'язок нерівності x∈(-4;-3,8).
Бачимо, що на інтервалі немає жодного цілого кореня.
Відповідь: x∈∅.

Це найпростіші логарифмічні нерівності, складні зводять заміною змінних до квадратних нерівностей, спрощують зведенням до однієї основи, логарифмуванням,  методом інтервалів і ...
Для цього Вам потрібно вивчити багато алгоритмів, на яких ми тут наголошуємо при аналізі відповідей до тестів.

Приклади обчислення логарифмічних нерівностей

Сьогодні проаналізуємо готові відповіді із курсу ЗНО підготовки. Але спершу розглянемо з десяток легких завдань.

Далі йдуть відповіді ЗНО тестів.

Приклад 17.1 Знайти множину розв’язків нерівності
log₃(x-4)≤log₃8.

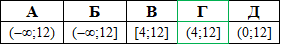
Розв'язування: Найпростішу логарифмічну нерівність розкриваємо шляхом опускання логарифмів та порівнянням виразів при рівних основах.
Перша нерівність x-4>0 є областю допустимих значень (ОДЗ) логарифма, у другій нерівності порівнюємо вирази з логарифмів. Знак в 2 нерівності залишили без змін, оскільки основа  більша за одиницю 3>1

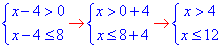
Позначимо результати 4<x≤12 на числову вісь

розв'язок x∈(4;12].
Відповідь: (4;12] – Г.

Приклад 17.2 Розв'язати нерівність
log_0,1x>log_0,1x.

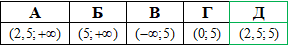
Розв'язування: Основа менша одиниці 0,1<1, тому знак при розкритті нерівності змінимо на протилежний.
ОДЗ для логарифмів дають 2 перші нерівності системи, третя – результат опускання логарифмів:

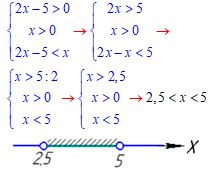
Інтервал розв'язків  x∈(2,5;5].
Відповідь: (2,5;5] – Д.

Приклад 17.3 Розв'язати нерівність
log_πx>log_π3+log_π5.

Розв'язування: За правилом суми логарифмів log_a(b)+log_a(c)=log(b•c) перетворимо праву сторону
log_πx>log_π(3•5),
log_πx>log_π15,
Оскільки основа більша одиниці π>1, то знак нерівності залишимо без змін,
з врахуванням ОДЗ (у І нерівності системи), отримаємо: 

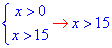
Будуємо множину розв'язків на числовій осі

та записуємо в інтервальній формі x∈(15;+∞).
Відповідь: (15;+∞) – А.

Приклад 17.7 Скільки цілих чисел є розв'язками нерівності
log_1/2(x+3)≥-1?

Розв'язування: За властивістю, що логарифм основи рівний одиниці, перетворимо праву сторону

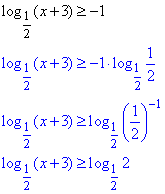
Основа 1/2<1.
З врахуванням ОДЗ логарифма x+3>0, отримаємо: 

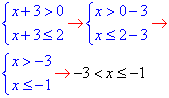
Будуємо множину розв'язків на числовій осі

x∈(-3;1].
Нерівність нестрога, тому справа в відповіді квадратна скобка.
Випишемо усі цілі розв'язки нерівності:
-2; -1.
Кількість =2.
Відповідь: два – Б.

Приклад 17.8 Розв'язати нерівність
log₈(3x-10)<1/3.

Розв'язування: Просимо зауважити, як можна звести логарифмічну нерівність до однієї основи

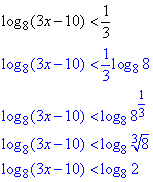
Даний метод далі буде часто повторюватися, тому – запамєтайте!
Виписуємо 1 умову на ОДЗ логарифма, 2 – розкриття нерівності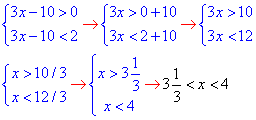

Наносимо множину розв'язків на числову вісь

звідси x∈(3 і 1/3;4).
Відповідь: (3 і 1/3;4) – Д.

Приклад 17.9 Вказати найбільший цілий розв'язок нерівності
log_1/7(x+3)>-1?

Розв'язування: Перетворимо праву сторону

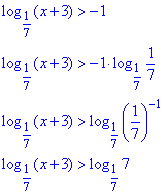
Основа логарифмів менша одиниці 1/7<1, тому знак при розкритті нерівності змінимо на протилежний.
Враховуючи ОДЗ логарифма (в І нерівності системи), отримаємо


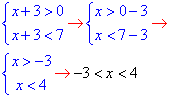
звідси x∈(-3;4).
x=3 - найбільший цілий розв'язок нерівності.
Відповідь: 3 – Г.

Приклад 17.26 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).

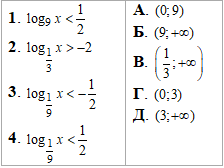
Розв'язування: Щоб в правій стороні утворити логарифм використовуємо формулу
1=log_aa.
Далі множники перед логарифмами вносимо степенями виразів під логарифмом за формулою
c•log_ab=log_ab^c.
Детальні обчислення наведені в таблиці:

Приклад 17.38 Розв'язати нерівність
log₂(5-x)log_x+1(1/8)≥-6.
У відповідь записати добуток усіх цілих розв'язків нерівності.
Розв'язування: Спростимо вираз log₂(5-x)log(x)·1/8:

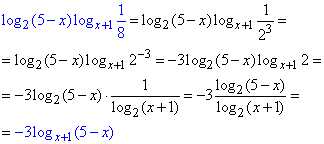
Підставляємо в нерівність

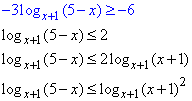
далі розкриваємо, враховуючи ОДЗ та знак нерівності для основ менших одиниці

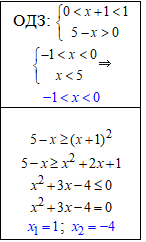
Наносимо усі знайдені точки + з ОДЗ на числову вісь та знаходимо множину розв'язків x∈(-1;0).

2) Випадок основи більшої за одиницю

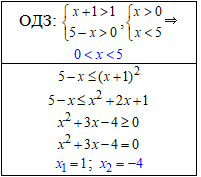
x∈[1;5).
Об'єднавши розв'язки останніх двох нерівностей, отримаємо
x∈(-1;0)∪[1;5).
Випишемо усі цілі значення та знайдемо їх добуток:
1; 2; 3; 4, тоді 1•2•3•4=24.
Відповідь: 24.

Переходьте до наступних уроків та вивчайте всі можливі схеми розкриття логарифмічних нерівностей.