Якщо Вам потрібно у швидкі терміни пригадати, як розкривати нерівності з логарифмами, тоді Вам до нас. Ми розв'язали та дослідили понад 50 прикладів із ЗНО тестів, знаємо які схеми обчислень слід застосовувувати при зведенні нерівностей до найпростішого типу. Нагадаємо, що основні перетворення полягають у зведенні логарифмів до однієї основи, а далі логарифми опускаємо та переходимо до простих нерівностей, знаки в яких розставляємо за правилом:
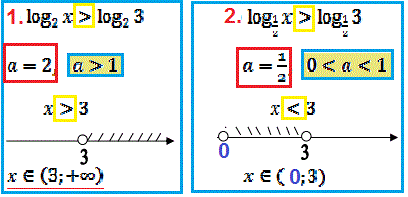
При спрощенні слід перевіряти ОДЗ та застосовувати ряд властивостей логарифма, про які піде мова в ході розрахунків.
Приклад 17.14 Розв’язати нерівність
log1/3(log5x)≥0.
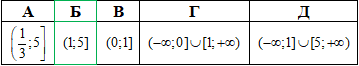
Розв'язування: Перетворимо та розкриємо нерівність за допомогою властивості, що логарифм одиниці рівний нулю
loga1=0.
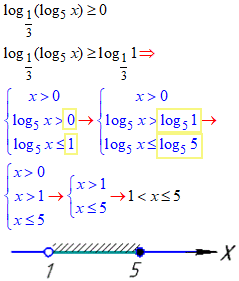
Розв'язок x∈(1;5].
Відповідь: (1;5] – Б.
Приклад 17.15 Скільки цілих розв'язків має нерівність?
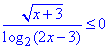
А | Б | В | Г | Д |
Жодного | один | два | три | більше, ніж три |
Розв'язування: Розглянемо вираз √(x+3):
ОДЗ кореня квадратного:
x+3≥0, тобто x≥-3.
Оскільки вираз √(x+3) (невід'ємний) для всіх x≥-3, то його знак, як множника, на нерівність не впливає.
Розглянемо вираз log2(2x-3):
ОДЗ логарифма:
2x-3>0;
log2(2x-3)≠0.
Нерівність еквівалентна системі нерівностей:
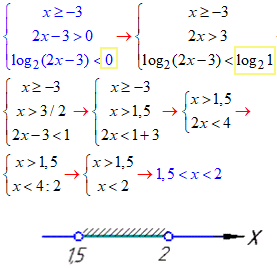
Множина розв'язків x∈(1,5;2).
Цілих значень серед розв'язків немає. Вибираємо варіант – жодного цілого розв'язку.
Відповідь: Жодного – А.
Приклад 17.17 Вказати цілі розв’язки нерівності
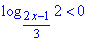
А | Б | В | Г | Д |
1; 2 | 1 | 0; 1 | 0; 1; 2 | 2; 3 |
Розв'язування: Логарифм одиниці рівний нулю при будь-якій основі, це правило застосуємо для перетворення правої частини
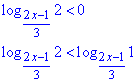
З того, що логарифм двійки менший логарифма одиниці слідує, що основа менша одиниці, тобто лежить в інтервалі:
1) 0<(2x-1)<3.
Цей момент Ви повинні розуміти.
Це означає, що змінна x задовольняє умову
2) Можете переконатися, що при умові (2x-1)/3>1 немає розв'язків,
Тоді знак нерівності залишимо без змін, опустимо логарифми
2<1.
отримали суперечність, тому нерівність при цій умові розв'язків немає.
З першого варіанту виписуємо множину розв'язків 0,5<x<2
звідси x∈(0,5;2).
Єдине цілим коренем нерівності є 1.
Відповідь: 1 – Б.
Приклад 17.25 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).
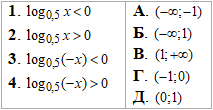
Розв'язування: При розкритті нерівностей використовуємо правило зміни знаку при основі меншій одиниці 0,5<1.
Для того, щоб звести до однієї основи застосуємо формулу 0=loga1.
Третя нерівність має розв'язки на інтервалі від мінус безмежності, тобто від'ємні значення. Зауважте, що таке можливо, якщо під логарифмом функція, яка дозволяє обчислювати його для від'ємних значень аргумета. Сам же логарифм визначений від нуля до плюс безмежності (див. графік).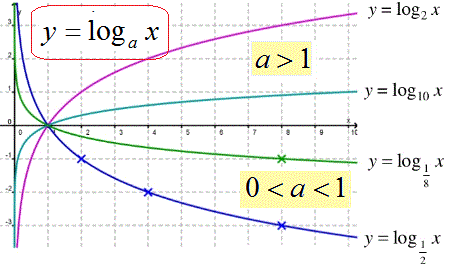
Приклад 17.18 Розв’язати нерівність
log9(x+3)2≤1.
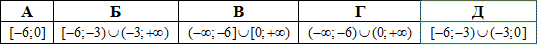
Розв'язування: Для перетворення правої сторони беремо формулу – логарифм основи рівний одиниці. Далі записуємо ОДЗ + нерівність, яку отримаємо при опусканні логарифмів
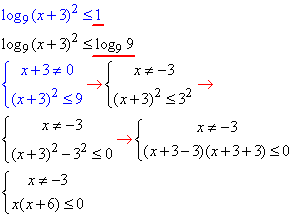
Останню нерівність розв'язуємо методом інтервалів
x(x+6)=0, тоді x1=0, x2=-6.
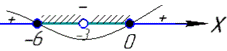
Розв'язок x∈[-6;-3)∪(-3;0].
Відповідь: [-6;-3)∪(-3;0] – Д.
Приклад 17.24 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).
Розв'язування: За властивістю, що логарифм одиниці рівний нулю, зводимо нерівності з логарифмом до однієї основи та розкриваємо:
Приклад 17.42 Дано функцію
f(x)=lg2x+lgx-3.
1) Знайти нулі функції. У відповідь записати найменше значення;
2) установити проміжки, де функція набуває від'ємних значень.
У відповідь записати найменше ціле значення.
Розв'язування: 1) Знайти нулі функції f(x) означає розв'язати рівняння:
lg2x+lgx-3=0.
ОДЗ: x>0.
Заміна: lg(x)=t
t2+2·t-3=0
за теоремою Вієта:
t1=1; t2=-3.
Пригадуємо заміну lg(x)=t та обчислимо прості логарифмічні нерівності
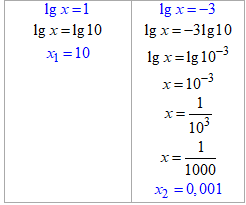
x1=10; x2=0,001 – нулі функції, x2=0,001 – найменше значення.
2) Установити проміжки, де функція f(x)=lg2x+lgx-3 набуває від'ємних значень означає розв'язати нерівність
lg2x+lgx-3<0.
Розв'язуємо методом інтервалів
t2+t-3=0;
t1=1, t2=-3
t∈(-3;1).
Повернемося до логарифмів lg(x)=t:
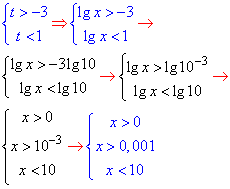
В підсумку 0,001<x<10.
Розв'язок x∈(0,001;10).
x=1– найменше ціле значення.
Відповідь: 1) 0,001; 2) 1.
Приклад 17.34 Розв'язати нерівність
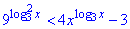
У відповідь записати суму всіх натуральних розв'язків нерівності.
Розв'язування: Спростимо вираз 9^(log3(x))2:
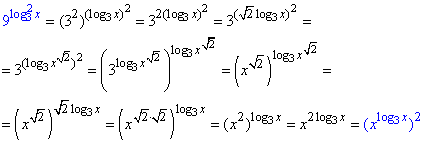
Зведемо нерівність до квадратної
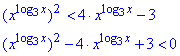
заміна: x^log3x=t, t>0,
t2-4t+3<0.
За методом інтервалів переходимо до р-ня
t2-4t+3=0,
де за теоремою Вієта:
t1=1; t2=3.
Наносимо точки на вісь та розставляємо знаки
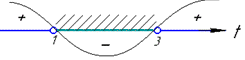
t∈(1;3).
Повернемося до заміни t=x^log3x та розпишемо логарифмічні нерівності:
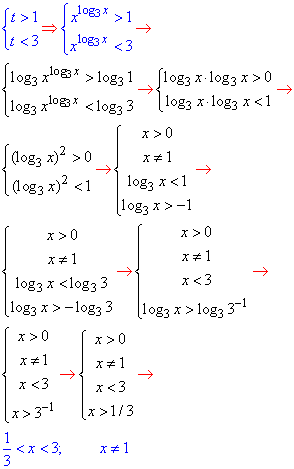
звідси x∈(1/3;1)∪(1;3).
Число 2 – єдиний натуральний розв'язок нерівності.
Відповідь: 2.
Як Ви могли переконатися, достатньо добре знати властивості логарифмів і можна самостійно навчитися перетворювати нерівності.
Більш прості завдання, включаючи теорію логарифмів за 11 клас Ви можете знайти на попередніх уроках. А далі розглянемо складні логарифмічні нерівності із ЗНО підготовки.
