Сьогодні проаналізуємо приклади на нерівності з модулями, кілька прикладів, що містять нерівності з дробами та двосторонні нерівності.
Завдання найбільш корисні для учнів, що готуються до ЗНО тестів з математики. Інші школярі можуть використовувати наведені готові відповіді для поглиблення практ
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 9. Цілі раціональні нерівності
Далі наведемо прості пояснення, як правильно розкривати нерівності з модулями? та що потрібно враховувати при спрощенні дробових та двосторонніх нерівностей?
Нерівності з модулями. Правила розкриття
Приклад 9.31 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).
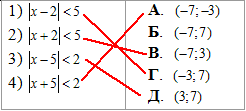
Обчислення: Маємо чотири нерівності з модулями. Розписуємо їх, як і у випадку мольних рівнянь.
Перше рівняння отримуємо, коли підмодульна функція додатна, друге - коли вона приймає від'ємне значення.
Як розв'язувати систему двох нерівностей детально описано на попередніх уроках + уважно перегляньте формули, що наведені далі.
1) |x-2|<5,
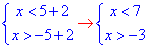
Спільні для обох інтервалів є точки x∈ (-3;7) - Г;

2) |x+2|<5,
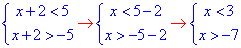
Записуємо шуканий інтервал x∈ (-7;3) - В;

3) |x-5| <2
Нерівність з модулем записуємо у вигляді
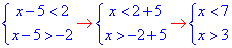
Спільними точками є значення x∈ (3;7) - Д;

4) |x+5|<2,
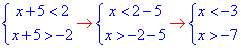
Розв'язком нерівності з модулями є інтервал x∈ (-7;-3) - А.

Приклад 9.32 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А – Д).
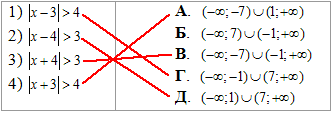
Обчислення: Маємо чотири строгі нерівності з модулями.
Підмодульні функції мають простий лінійний вигляд, що значно спрощує знаходження коренів.
Обчислення зводяться до систем двох нерівностей, перетворення яких детально розписані в наступних формулах
1) |x-3|<4,
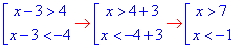
Розв'язком нерівності з модулем є два інтервали x∈ (-∞;-1)∪(7;+∞) - Г;
На числовій осі вони матимуть вигляд

2) |x-4|>3,
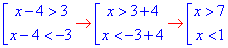
звідси нерівність з модулями задовільняють точки x∈ (-∞;1)∪(7;+∞) - Д;

3) |x+4|>3,
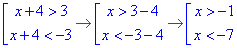
Отримали у відповідь наступні значення x∈ (-∞;-7)∪(-1;+∞) - В;
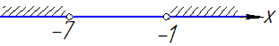
4) |x+3|>4,
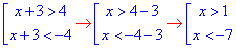
Інтервали, що є розв'язком нерівності з модулем відобразимо на числовій осі

x∈ (-∞;-7)∪(1;+ ∞) - А.
На готових відповідях до ЗНО тестів Ви можете взяти для себе багато нової і легкої в плані вивчення корисної практичної інформації. Наведені схеми обчислень застосовуйте на практиці.
Приклад 9.33 Розв'язати нерівність
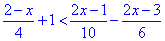
У відповідь записати найменший цілий розв'язок.
Обчислення: Останні тестові завдання для підготовки до ЗНО тестів з математики найважчі. Вони вимагають від Вас доброї уваги, оскільки мова піде про маніпуляції з дробами, які необхідні для зведення до спільного знаменника та вираження змінної "ікс" із нерівності.
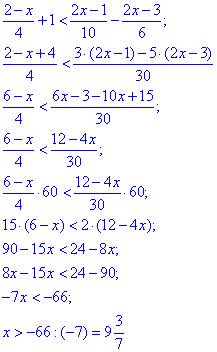
В результаті прийдемо до інтервалу x∈ (66/7;-5).
Звідси слідує, що число 10 є найменшим цілим розв'язком нерівності.
Відповідь: 10.
Приклад 9.34 Розв'язати нерівність 7<1-3x<16.
У відповідь записати найменший цілий розв'язок.
Обчислення: Двосторонню нерівність розписуємо у вигляді системи, а далі по черзі знаходимо обмеження на "ікс" для кожної з нерівностей
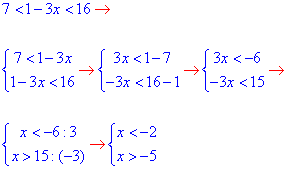
Спільним перетином є інтервал x∈ (-5;-2).

Звідси слідує, що число -3 є найбільшим цілим розв'язком нерівності.
Точку x=2 не задовільняє умові, оскільки нерівність строга.
Відповідь: -3.
Приклад 9.35 Розв'язати нерівність x+1<x/2<x+2.
У відповідь записати суму цілих розв'язків.
Обчислення: Зводимо нерівність до системи двох, а далі через елементарні перетворення над дробами знаходимо умови, що накладають обмеження на змінні "ікс"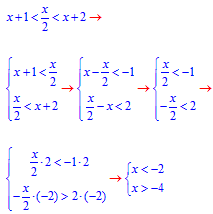
звідси змінна належить інтервалу x∈ (-4;-2).
Корені нерівності відображаємо на числовій осі. 
Оскільки нерівність строга, то єдине ціле число, що входить у розв'язок нерівності є число -3.
Відповідь: -3.
Думаємо, що готових прикладів на раціональні нерівності достатньо для підготовки до ЗНО тестів. Далі все залежить від Вашого бажання вчитися та працювати самостійно.
Виконайте по 5-10 прикладів на домашню роботу з аналогічними умовами до наведених і Ви точно знатимете, що робити на Тестах та екзаменах!



