На попередньому уроці Ви познайомилися з методом інтервалів для розкриття нерівностей, сьогодні роглянемо нерівності з параметром, дробові та квадратичні нерівності. На остатньому занятті резберемо випадок, коли нерівність містить модуль.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 9. Цілі раціональні нерівності
Рівняння та нерівності з параметром вважають одними із найскладніших як в школі так і ВУЗ-ах.
А все тому, що умова ділиться на кілька варіантів і є більше шансів допустити помилку в порівняння з простими завданнями.
Тому не спішіть і уважно прочитайте всі пояснення до наведених тестових завдань.
Розкриття нерівностей з параметром
Приклад 9.20 За яких значень параметра a розв'язком нерівності (a-3)x≤7 є проміжок [7/(a-3) ;+ ∞)?
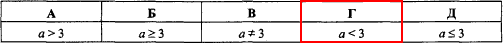
Обчислення: Переходимо до нерівностей з параметром. Для багатьох із школярів, та й для студентів також, такі завдання вважають одними з найскладніших на тестах чи екзаменах. Тому будьте уважні, та дочитайте наведені тут відповіді.
Якщо a-3=0, тобто a=3, то маємо 0•x≤7, отже 0≤7 для всіх x (x∈R);
якщо a-3>0, тобто a>3, то маємо x≤7/(a-3), отже x∈(- ∞;7/(a-3));
якщо a-3<0, тобто a<3, то маємо x ≥7/(a-3), (тому що ми ділимо на від'ємне число і тому змінили знак нерівності).
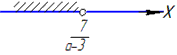
Звідси слідує, що при a<3 розв'язком нерівності (a-3)x≤7 є проміжок [7/(a-3) ;+ ∞).
Відповідь: a<3 – Г.
Приклад 9.21 Знайти значення параметра a, за якого розв'язком нерівності 3x-1<ax+5 є усі дійсні числа.
Обчислення: Перепишемо нерівність з параметром, попередньо виділивши всі сталі при змінній "ікс"
3x-1<ax+5,
3x-ax<1+5,
(3-a)x<6.
Далі, в залежності від значення параметра а, можливі наступні випадки:
якщо 3-a>0,
3>a, тобто a<3, то маємо x<6/(3-a), отже x∈(- ∞;6/(3-a));
якщо 3-a,
тобто a>3, то маємо x>6/(3-a), отже x∈(6/(3-a);+ ∞);
( ми ділили на від'ємне число і тому змінили знак нерівності на протилежний).
Якщо маємо рівність нулю 3-a=0,
тобто a=3, то маємо 0•x<6, отже 0<6 для всіх x (x∈R).
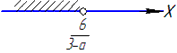
Звідси слідує, що при a=3 розв'язком нерівності 3x-1<ax+5 є усі дійсні числа.
Відповідь: 3 – А.
Приклад 9.22 Знайти множину розв'язків нерівності (x-4)(a-x)≥0, якщо параметр a<4.
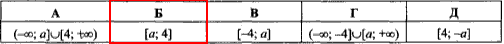
Обчислення: Помножимо нерівність на мінус одиницю та поміняємо її знак. При цьому одну з дужок змінимо так, щоб коефіцієнт при "ікс" був додатний
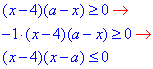
(змінили знак нерівності!)
Розв'яжемо відповідне рівняння:
(x-4)(x-a)=0, звідси x1=4 і x2=a<4, отже , тобто x∈[a;4].
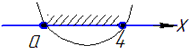
Тут уважно розберіться чому саме так вийшло, та наскільки проста дана схема на практиці.
Відповідь: [a;4] – Б.
Приклад 9.23 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А – Д).
1) 5x>30
2) -5x>30
3) 5x<30
4) -5x<30
А. (-∞;-6);
Б. (-∞;6);
В. (-6;+∞);
Г. (-6;6)
Д. (6; +∞).
Обчислення: Маємо просте тестове завдання, яке для одних учнів просте, бо вони добре знають нерівності.
Інші - "не пройдуть тести" через незнання елементарного правила зі зміни знаку нерівності, або питання "Що буде, якщо обидві частини помножити на мінус одиницю?".
А відповідь до всього криється в наступних перетвореннях нерівностей
1) 5x>30,
x>30:5, звідси x>6,
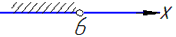
тобто x∈(6; +∞) - Д;
2) -5x>30,
x<30:(-5), звідси x<-6,
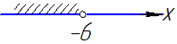
тобто x∈(-∞;-6) - А;
3) 5x<30,
x<30:5, звідси x<6,
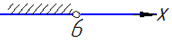
тобто x∈(-∞;6) - Б;
4) -5x<30,
x>30:(-5), звідси x>-6,
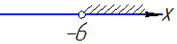
тобто x∈(-6; +∞) - В.
Ось такі короткі пояснення до простих завдань.
Приклад 9.24 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А – Д).
1) (x-1)/3<1
2) (x+1)/3<1
3) (-x+1)/3<1
4) (-x-1)/3<1
А. (-∞;-4)
Б. (-∞;2)
В. (-∞;4)
Г. (-4;+∞)
Д. (-2;+∞)
Обчислення: Задане тестове завдання більше на уважність та на вміння переносити вирази за знак нерівності, а воно ідентичне до правила переносу за знак рівності (=).
1) (x-1)/3<1,
x-1<3,
x<3+1 звідси x<4,
тобто x∈(-∞;4) - В;
2) (x+1)/3<1,
x+1<3,
x<3-1 звідси x<2,
тобто x∈(-∞;2) - Б;
3) (-x+1)/3<1,
-x+1<3,
-x<3-1, -x<2, звідси x>-2,
тобто x∈(-2;+∞) - Д;
4) (-x-1)/3<1,
-x-1<3,
-x<3+1,
-x<4, звідси x>-4,
тобто x∈(-4;+∞) - Г.
Пояснень тут мінімум, оскільки завдання за 9 клас і все має бути Вам зрозумілим.
Приклад 9.25 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А – Д).
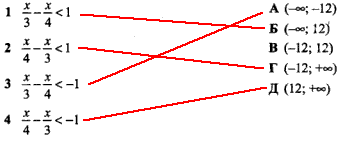
Обчислення: На попередніх та наступних прикладах, якщо їх уважно читати, можна за малий час навчитися будувати інтервали на осі та правильно обчислювати прості раціональні нерівності.
1) Зведемо дроби до спільного знаменника та виразимо "ікс"
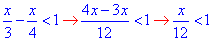
звідси x<12,
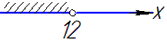
тобто отримали інтервал x∈(-∞;12) - Б;
2) Виконуємо ті ж самі маніпуляції з дробовими виразами
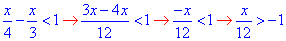
звідси x>-12,
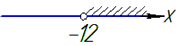
тобто x∈(-12;+∞) - Г;
3) 
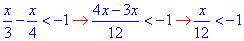, звідси x<-12,
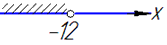
тобто x∈(-∞;-12) - А;
2) 
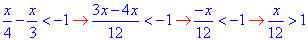, звідси x>12,
тобто x∈(12;+∞) - Д.
Звідси бачимо як легко викладачеві придумати для школярів чи студентів нове завдання на нерівності. Достатньо поміняти знак нерівності чи один знак перед виразом і отримаємо інший інтервал у відповідь.
Приклад 9.26 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А – Д).
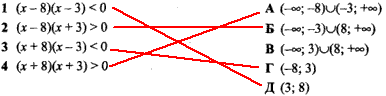
Обчислення: Ліву сторону прирівнюємо до нуля та визначаємо точки де функція перетинає вісь Ox. Далі підстановкою нуля, чи іншого числа, простого в плані визначення знаку функції, знаходимо проміжки знакосталості та наносимо їх на числову вісь.
1) (x-8)(x-3)<0,
(x-8)(x-3)=0, звідси x1=3 і x2=8, тобто x∈(3;8) - Д;
2) (x-8)(x+3)>0,
(x-8)(x+3)=0, звідси x1=-3 і x2=8, тобто x∈(-∞;-3)∪(8;+ ∞). - Б;
3) (x+8)(x-3)<0, (x+8)(x-3)=0, звідси x1=-8 і x2=3, тобто x∈(-∞;3) - Г;
4) (x+8)(x+3)>0, (x+8)(x+3)=0, звідси x1=-8 і x2=-3, тобто x∈(-∞;-8)∪(-3;+∞). - А.
Якщо знаки при "іксах" додатні, то всюди матимемо параболи з вітками вгору. Далі не важко виписати один або два інтервали де функція приймає або додатні, або від'ємні значення.
Приклад 9.27 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).
Обчислення: Ще одне завдання на вміння розписувати квадратичні нерівності.
Вони не важкі, оскільки мають всього два корені кратності один.
1) (x-2)(x+3)<0,
(x-2)(x+3)=0, звідси x1=-3 і x2=2, тобто x∈(-3;2) - Г;
2) (2-x)(x+3)<0,
(x-2)(x+3)>0, (x-2)(x+3)=0, звідси x1=-3 і x2=2, тобто x∈(-∞;-3)∪(2;+∞) - А;
3) (x+2)(x-3)<0,
(x+2)(x-3)=0, звідси x1=-2 і x2=3, тобто x∈(-2;3) - Д;
4) (x+2)(3-x)<0,
(x+2)(x-3)>0,
(x+2)(x-3)=0, звідси x1=-2 і x2=3, тобто x∈(-∞;-2)∪(3;+∞) - Б.
Приклад 9.28 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А – Д).
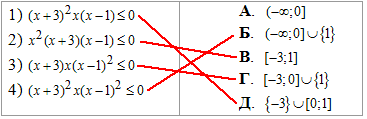
Обчислення: Як бачимо всі задані нерівності нестрогі, тому граничні точки будемо включати у розв'язок. Якщо вираз (x-a)^2 стоїть у квадраті, то крива свій знак не змінює при переході через точку x=a.
1) (x+3)^2x(x-1) ≤0,
(x+3)^2x(x-1)=0, звідси x1=-3, x2=0 і x3=1. тобто x∈{-3}∪[0;1] - Д;
2) x^2(x+3)(x-1) ≤0,
x^2(x+3)(x-1)=0, звідси x1=-3, x2=0 і x3=1. тобто x∈[-3;1] - В;
3) (x+3)x(x-1)^2≤0,
(x+3)x(x-1)^2=0, звідси x1=-3, x2=0 і x3=1. тобто x∈ [-3;0] ∪{1} - Г;
4) (x+3)^2x(x-1)^2≤0,
(x+3)^2x(x-1)^2=0, звідси x1=-3, x2=0 і x3=1. тобто x∈ [-∞;0] ∪{1} - Б.
Зведення квадратичних нерівностей до системи двох
Приклад 9.29 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А – Д).
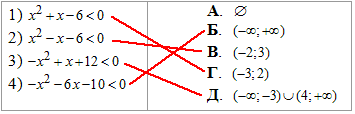
Обчислення: Тут в лівій частині нерівностей маємо квадратне рівняння, тому щоб розв'язати його знаходимо дискримінант або застосовуємо формули Вієта.
1) x^2+x-6<0,
x^2+x-6=0,
D=1-4•1•(-6)=25=5^2,
звідси x1=-3 і x2=2, тобто x∈ (-3;2) - Г;
Для повної картини до кожного пункту завдання наводимо рисунок числової осі з заштрихованим шуканим інтервалом.
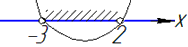
2) x^2-x-6<0,
x^2-x-6=0,
D=25, звідси x1=-2 і x2=3, тобто x∈ (-2;3) - В;
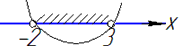
3) –x^2+x+12<0,
–x^2+x+12=0,
D=1-4•(-1)•12=49=7^2, звідси x1=-3 і x2=4, тобто (-∞;-3)∪(4;+ ∞) - Д;
В цій нерівності отримали параболу з гілками вниз, оскільки перед змінною x^2 стоїть -1.
4) –x^2-6x-10<0,
–x^2-6x-10=0,
D=1-4•(-1)•(-10)=-4<0, (рівняння не має коренів, оскільки дискримінант від'ємний D<0).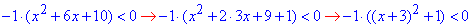 
Бачимо, що яке б не було значення змінної "ікс" вираз –x^2-6x-10 все одно буде менше нуля, тому розв'язком нерівності –x^2-6x-10 <0 є всі дійсні числа, тобто (-∞;+∞) - Б.
Приклад 9.30 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).
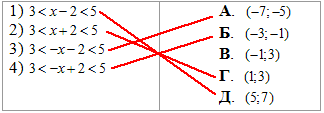
Обчислення: Маємо двосторонні нерівності.
В попередніх прикладах показано, що їх слід звести до системи двох нерівностей і у відповідь записати інтервал, який є перетином двох знайдених.
1) 
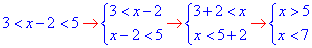
Звідси x∈ (5;7) - Д;
2) 
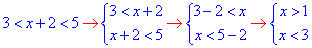
Отримали x∈ (1;3) - Г;
3) 
,
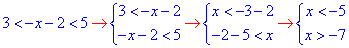Коренями нерівності будуть значення x∈ (-7;-5) - А;
4) 
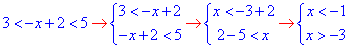
Перетином двох інтервалів будуть точки, що належать x∈ (-3;-1) - Б.
Ще 5 прикладів, що містять пояснення до нерівностей з модулями детально розберемо далі.
