Після перегляду раціональних нерівностей можемо переходити до більш складних в плані обчислень дробових нерівностей.
Схема обчислень полягає в перенесенні всіх доданків по одну сторону від знаку нерівності, щоб з іншої отримати нуль.
Далі доданки потрібно звести до одного дробу. Отриманий вираз заміняємо рівносильною нерівністю та умовою обмеження на нулі знаменника.
Далі всі дії ідентичні як і у випадку раціональних нерівностей, застосовуємо метод інтервалів, властивості лінійних та квадратичних функцій.
Методика обчислень дробових нерівностей не надто складно, і в цьому Ви скоро переконаєтесь.
Завдання підібрано з довідника для підготовки до ЗНО тестів, тому вони будуть корисними як для школярів так і випускників, що готуються до вступу у ВУЗ-и.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 11. Дробові раціональні нерівності
Тестові задачі розміщенні за зростанням складності, спершу йдуть легкі (8-9 клас), далі складніші (10-11 класи).
Приклад 11.1 Знайти множину розв'язків нерівності x+1/x>1/x-2.
Обчислення: Пояснення до завдань організовано так, щоб донести Вам найнеобхіднішу інформацію. Все решта винесено в формули
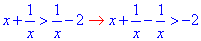
Оскільки у нерівності міститься дріб знаменник якого не повинен дорівнювати нулю, то задана нерівність рівносильна системі:
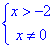
Маємо строгу нерівність, тому знайдені точки "виколюємо" на числовій осі, а далі заштриховуємо множину розв'язків
В результаті отримаємо значення з інтервалів x∈ (-2;0)∪(0;+∞).
Помилкою в обчисленнях був би варіант, коли Ви спрощуєте подібні доданки в обох частинах (1/x), але не вказуєте, що на нуль ділити не можна.
Про це завжди пам'ятайте!
Відповідь: (-2;0)∪(0;+∞) – В.
Приклад 11.2 Вибрати нерівність, множиною розв'язків якої є всі дійсні числа R.
Обчислення: В першій нерівності з множини розв'язків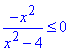 
слід одразу вилучити нулі знаменника дробу, тобто точки x1≠-2 і x2≠2. Звідси слідує, що у відповідь не отримаємо x∈R);
Друга дробова нерівність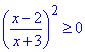 
накладає обмеження на множини розв'язків у вигляді x≠3, тому також не підходить під умову завдання;
Третю нерівність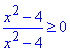 
помилково можна замінити еквівалентною 0≥0, але це неправильно.
Тому з множини розв'язків слід виколоти точки x1≠2 і x2≠2, а значить всієї числової осі не отримаємо;
Варіант Г) також відпадає, оскільки нерівність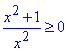 
точкою x≠0 розбиває множини розв'язків на два інтервали - до нуля, та після нуля;
Залишається п'ята нерівність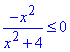 
ліва сторона при всіх значеннях крім нуля буде від'ємною.
Знаменник ні при яких значень x не дорівнює нулю, бо рівняння x^2+4=0 не має розв'язків, а при x=0 маємо:
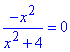
тому множиною розв'язків нерівності є всі дійсні числа, тобто x∈R, або x∈(-∞;+∞).
Відповідь: Д.
Приклад 11.3 Вибрати нерівність, множиною розв'язків якої є порожня множина.
Обчислення: Перша нерівність еквівалентна наступній
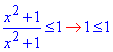
тому виконується при будь-яких x∈R (x≠∅);
Слід зауважити, що знаменник не має особливості, оскільки завжди додатний.
Дробову нерівність Б) можна перетворити до вигляду
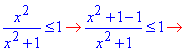
-1/(x^2+1) ≤0.
Нерівність справедлива для всіх точок числової осі x∈R (x≠∅);
Розпишемо нерівність В)
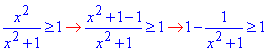
Другий доданок 1/(x^2+1)>0 завжди додатний, тому ні при яких значень x, нерівність
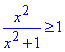не має розв'язків, тобто x∈∅.
Отже ми знайшли випадок, коли множиною розв'язків нерівності є порожня множина.
Останні два варіанти можна не перевіряти, але оскільки наша мета якісно підготувати Вас до ЗНО тестів, то наведемо пояснення і до них.
Нерівність Г) еквівалентна тотожності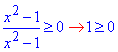 
тому справедлива при будь-яких x, крім нулів знаменника (x≠1,x≠1).
Випадок Д) можемо перетворити до вигляду
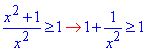
Звідси легко зробити висновок, що умова виконується при будь-яких x, крім нуля знаменника x≠0.
Відповідь: В.
Після перегляду готових відповідей лише до трьох прикладів можемо зробити висновок, що більшість помилок допускається внаслідок спрощення дробів і не врахуванні нулів знаменників дробів. Тому Вам перша порада на майбутнє:
не спішіть спрощувати дроби в нерівностях, спершу виписуйте обмеження на знаменники, а далі виконуйте перетворення нерівностей.
Приклад 11.4 Розв'язати нерівність x/(x-5) ≥0.
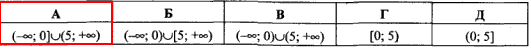
Обчислення: Задана нестрога нерівність
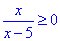
за знаком еквівалентна системі з нерівності та умови на знаменник:
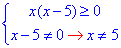
Розв'яжемо нерівність x(x-5)≥0.
Ліва сторона перетворюється в нуль при значеннях x1=0 і x2=5.
Рівняння описує параболу з вітками вгору, тому множиною розв'язків будуть точки за межами знайдених
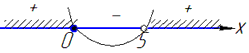
тобто x∈(-∞;0]∪(5;+∞).
Нерівність не строга, але слід врахувати, що x≠5.
Відповідь: (-∞;0]∪(5;+∞) – А.
Приклад 11.5 Розв'язати нерівність (x+5)/(x-2)≤0.
Обчислення: Маємо нестрогу дробову нерівність, яка еквівалентна системі:
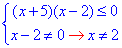
Для того, щоб розв'язати нерівність (x+5)(x-2)≤0
записуємо відповідне їй рівняння:
(x+5)(x-2)=0.
Звідси легко визначити точки x1=-5 і x2=2.
Далі наносимо їх на числову вісь.
Підстановкою точки (найкраще х=0) знаходимо, що всередині значення виразу (x+5)(x-2) від'ємні, а за межами чергуються, тобто змінюються на "+".
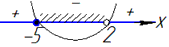
Записуємо множину розв'язків нерівності x∈[-5;2).
Не забувайте враховувати обмеження на нулі знаменника x≠2.
Відповідь: [-5;2) – Г.
Приклад 11.6 Розв'язати нерівність
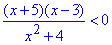
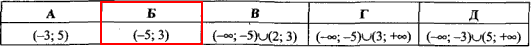
Обчислення: Як бачимо, ні при яких x знаменник x^2+4 не перетворюється на 0 і залишається завжди додатним (x^2+4>0 при x∈R), тому дробова нерівність еквівалентна чисельнику меншому нуля
(x+5)(x-3)<0.
Розв'яжемо нерівність, для цього запишемо відповідне рівняння:
(x+5)(x-3)=0.
Звідси, маємо дві точки x1=-5 і x2=3 , які розбивають числову вісь на три інтервали.
Підстановкою нуля визначаємо знак функції між знайденими точками.
Множиною розв'язків є інтервал x∈(-5;3).
Відповідь: (-5;3) – Б.
Приклад 11.7 Розв'язати нерівність (x+5)/(x^2-4)≤0.
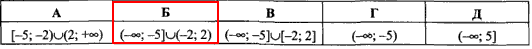
Обчислення: Нерівність заміняємо еквівалентною системою та розписуємо:
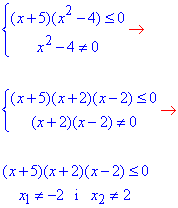
Розв'яжемо нестрогу нерівність (x+5)(x+2)(x-2) ≤0.
Рівняння (x+5)(x+2)(x-2)=0 розв'язком має три точки x1=-5, x2=-2 і x3=2.
Наносимо їх на числову вісь.
Далі на одному з проміжків визначаємо знак, а на всіх сусідніх - знаки змінюємо за правилом чергування з "+" на "-", та з "-" на "+".
Розв'язком будуть два інтервали x∈(-∞;-5]∪(-2;+ 2).
Нагадуємо, щоб Ви врахували нулі знаменника x1≠-2 і x2≠2. Ці точки на числовій осі будуть виколотими.
Відповідь: (-∞;-5]∪(-2;+ 2) – Б.
Приклад 11.8 Розв'язати нерівність (x+5)/(x+3)>1.
Обчислення: Розпишемо дробову нерівність, перенісши одиницю в ліву сторону
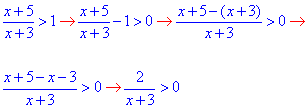
Отримали просту строгу нерівність, яку можемо замінити еквівалентною:
x+3>0, звідси x>-3.
Такі маніпуляції допустимі, оскільки нас цікавить знак функції на інтервалі, а не її значення.
Зобразимо отриману умову на числовій осі
Далі множину коренів записуємо інтервалом x∈(-3;+∞).
Відповідь: (-3;+∞) – В.
Приклад 11.9 Розв'язати нерівність (3x+4)/(x+1)≤2.
Обчислення: Схема перетворень аналогічна до попереднього завдання:
переносимо двійку в ліву частину нерівності та спрощуємо дріб
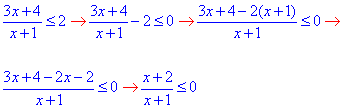
Оскільки отримана нерівність нестрога, то її можемо замінити системою:
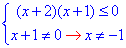
Запишемо рівняння для визначення нулів нерівності:
(x+2)(x+1)=0.
Звідси, x1=-2 і x2=-1.
Графіком буде парабола з вітками вгору, тому на числовій осі функція матиме наступні знаки
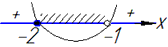
Інтервал x∈[-2;-1) є множиною розв'язків нерівності з дробом.
Відповідь: [-2;-1) – В.
Далі будуть розв'язані більш складні тестові приклади, що передбачають обчислення дробових нерівностей з параметром та модулями.
Тому уважно розберіть наведені вище правила, без них важко буде зрозуміти застосування правил переносу та заміни дробових нерівностей рівносильними раціональними на практиці.
