Метод заміни дробової нерівності раціональною детально описано на попередньому уроці.
Тут продовжуємо аналізувати готові відповіді до тестових завдань на дробові нерівності та обчислювати щоразу складніші приклади.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 11. Дробові раціональні нерівності
Наведені далі завдання відповідають шкільній програмі за 9-10 класи шкільної програми.
Приклад 11.10 Розв'язати нерівність 1/x≤x.
Обчислення: Виконуємо перетворення над дробом
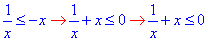
(1+x^2)/x≤0.
Як бачимо, вираз 1+x^2 не перетворюється на 0 і залишається завжди додатним (1+x^2>0 при x∈R), тому задана нерівність еквівалентна нерівності x<0.
(нерівність стала строгою, бо знаменник не дорівнює нулю, x≠0).
Зобразимо множину розв'язків на числовій осі
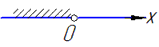
та записуємо інтервалом x∈(-∞;0).
Відповідь: (-∞;0) – Г.
Приклад 11.11 Розв'язати нерівність 3/x≤2/(x+1).

Обчислення: Переносимо один з дробів так, щоб за знаком нерівності або перед ним отримати нуль.
Далі зводимо все під спільний знаменник
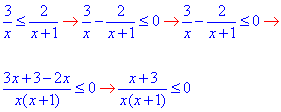
Оскільки нерівність нестрога, то її замінюємо еквівалентною системою із нерівності та умови на знаменник:
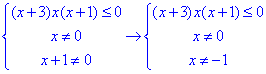
розв'яжемо нерівність (x+3)x(x+1) ≤0.
Для цього випишемо рівняння
(x+3)x(x+1)=0, яке справедливе при коренях x1=-3, x2=-1 і x3=0.
Нанесемо їх на числову пряму і побудуємо інтервали.
В одиниці f(1)=(1+3)1(1+1)=8>0 знак додатний, тому на крайньому правому інтервалі він теж додатний.
При переході на сусідні інтервали знак буде чергуватися з "плюса" на "мінус" і т.д.
Рисунок числової осі з проміжками знакосталості наведено далі
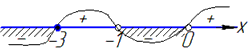
У розв'язок записуємо множину точок, де функція приймає від'ємні значення або рівна нулю
x∈(-∞;-3] ∪(-1;0).
Відповідь: А.
Приклад 11.12 Знайти множину розв'язків нерівності 3/(x-3)>1/(x+2).

Обчислення: Спершу нерівність перетворюємо, звівши дроби з однієї сторони від знаку.
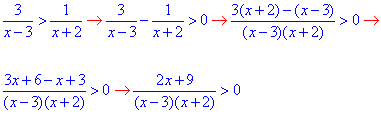
Отриману строгу нерівність можна замінити еквівалентною:
(2x+9)(x-3)(x+2)>0, або 2(x+4,5)(x-3)(x+2)>0.
Її нулями є точки x1=-4,5, x2=-2 і x3=3.
Нанесемо їх на числову пряму і побудуємо інтервали. В нулі (x=0) знак від'ємний, далі чергується.

Розв'язком нерівності є два інтервали x∈(-4,5;-2)∪(3;+ 1).
Відповідь: (-4,5;-2)∪(3;+ 1) – В.
Приклад 11.13 Знайти множину розв'язків нерівності
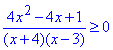

Обчислення: Зведемо чисельник дробу до однієї з формул спрощеного множення
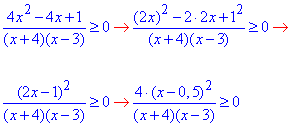
Оскільки нерівність нестрога, то її замінюємо еквівалентною системою:
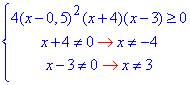
Розв'яжемо нерівність 4(x-0,5)^2(x+4)(x-3)≥0.
для цього знайдемо корені відповідного рівняння:
4(x-0,5)^2(x+4)(x-3)=0, звідси отримаємо x1=-4, x2=0,5 і x3=3.
Нанесемо їх на числову пряму і побудуємо інтервали.
Як бачимо, вираз (x-0,5)^2 має парний степінь, тому крива свій знак змінювати не буде при проходженні через точку x2=0,5. Це важливе правило, яке спрощує визначення інтервалів знакосталості функції.

Отримали два інтервали та точку x∈(-∞;-4)∪{1/2}∪ (3;+∞).
Точка x=0,5 (або x=1/2) увійшла у розв'язок заданої нерівності (є нулем чисельника)!
Запам'ятайте, що окремі точки в нерівностях виділяють фігурними дужками {}.
Відповідь: (-∞;-4)∪{1/2}∪ (3;+∞) – Г.
Приклад 11.14 Розв'язати нерівність
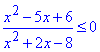

Обчислення: Оскільки нерівність нестрога, то задана нерівність еквівалентна системі:
(x^2-5x+6)(x^2+2x-8)≤0;
(x^2+2x-8)≠0.
Розв'яжемо відповідне рівняння:
(x^2-5x+6)(x^2+2x-8)=0.
x^2-5x+6=0
і x^2+2x-8=0.
За теоремою Вієта встановлюємо, що x1=3, x2=x3=2 і x4=-4.
Отже систему можна переписати наступним чином:
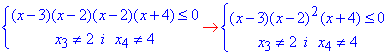
Легко бачити, що вираз (x-2)^2 має парний степінь, тому крива свій знак змінювати не буде при проходженні через точку x=2.

тобто x∈(-4;2)∪(2;3].
Точка x=2 не увійшла, а x=3 увійшла у розв'язок заданої нерівності!
Відповідь: (-4;2)∪(2;3] – Б.
Приклад 11.15 Обчислити найменший цілий розв'язок нерівності
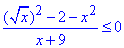

Обчислення: Оскільки нерівність нестрога і під коренем міститься x, то маємо записуємо еквівалентну систему нерівностей
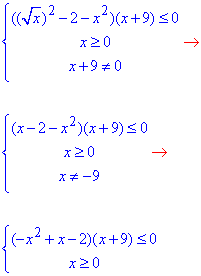
Розв'яжемо нерівність:
(-x^2+x-2)(x+9)≤0.
Помножимо першу дужку на -1 і змінимо знак нерівності на протилежний:
(x^2-x+2)(x+9)≥0.
Розв'яжемо квадратне рівняння через дискримінант:
x^2-x+2=0,
D=(-1)^2-4*1*2=1-8=-7
Він від'ємний (D<0), отже рівняння x^2-x+2=0 коренів не має.
Але це не значить, що на цьому всі обчислення.
Виділимо повний квадрат, щоб з'ясувати знак виразу
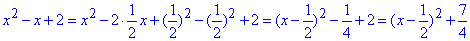
Робимо висновок, що вираз x^2-x+2>0 більше нуля для будь-яких x.
Тому нерівність (x^2-x+2)(x+9)≥0 еквівалентна нерівності (x+9)≥0.
Звідси x≥-9.
Але, враховуючи обмеження на кореневу функцію, яку отримали на початку, множина розв'язків нерівності звузиться до значень x≥0

Записуємо знайдений інтервал x∈[0;+∞).
Як бачимо, найменший цілий розв'язок заданої нерівності є число 0.
Хто не врахував обмежень на корінь міг у відповідь отримати -9, але це неправильно.
Відповідь: 0 – В.
Приклад 11.16 Розв'язати нерівність
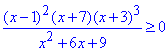
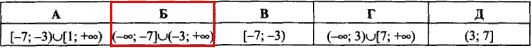
Обчислення: Перепишемо знаменник дробу за формулою квадрату суми
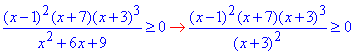
Нестрогу нерівність можна замінити еквівалентною системою:
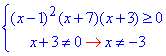
Розв'яжемо відповідне рівняння:
(x-1)^2(x+7)(x+3)=0.
Звідси, x1=-7, x2=-3 і x3=1.
Вираз (x-1)^2 має парний степінь, тому крива свій знак змінювати не буде при проходженні через точку x=1.
В точці x=-3 має кубічну степінь, тому при переході знак не змінюється.

Множиною розв'язків нерівності є два інтервали x∈(-∞;-7]∪(-3;+∞).
Точка x=1 належить (-3;+∞), тобто увійшла у розв'язок заданої нерівності!
Відповідь: (-∞;-7]∪(-3;+∞). – Б.
Приклад 11.17 Знайти кількість цілих розв'язків нерівності
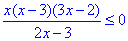

Обчислення: Маємо нестрогу дробову нерівність яку замінюємо еквівалентною системою:
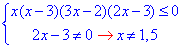
Випишемо нулі рівняння:
x(x-3)(3x-2)(2x-3)=0.
звідси чотири точки x1=0, x2=2/3, x3=1,5 і x4=3.

Отримали один інтервал та один проміжок x∈[0;2/3]∪(3/2;3].
До цілих розв'язків заданої нерівності належать числа 0, 2 і 3, тому маємо три цілих розв'язки нерівності.
Відповідь: 3 – В.
Приклад 11.18 Розв'язати нерівність
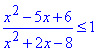
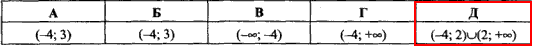
Обчислення: Переносимо одиницю в ліву сторону та спростимо сумарний дріб
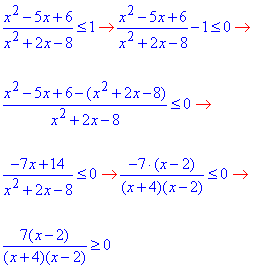
(Тут помножили на -1 та змінили знак).
Отриману дробову нерівність еквівалентна системі:
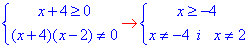
Виколюємо точки на числовій осі та встановлюємо інтервали де нерівність виконується.

Отримали два інтервали x∈(-4;2)∪(2;+∞).
Відповідь: (-4;2)∪(2;+∞). – Д.
Далі розглянемо складні дробові нерівності, що містять в умові модулі або параметри.
Рекомендуємо прочитати весь цикл публікацій на нерівності, щоб бути готовими до будь-яких завдань з цієї теми на ЗНО тестах.



