Алгоритм переходу від дробової нерівності до рівносильної раціональної описано на попередніх уроках.
Тут розберемо випадки коли дробові функції містять модулі, а також дробові нерівності з параметром.
Перегляньте готові відповіді до прикладів, щоб бути готовими до таких завдань на ЗНО тестуванні.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 11. Дробові раціональні нерівності
Наведені далі завдання потрібно виконувати не спішачи, оскільки можна "наламати дров" та не дійти до правильної відповіді.
Приклад 11.19 Знайти множину розв'язків нерівності |1/(x-5)|>1.
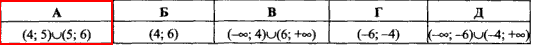
Обчислення: Дробову нерівність містить модуль
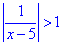
тому її необхідно розділити та записати у вигляді сукупності нерівностей:
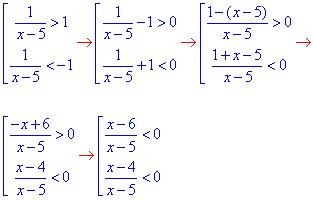
Подальші перетворення ідентичні до уже розглянутих на попередніх уроках випадків.
Строгі нерівності замінюємо еквівалентними простими:
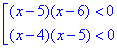
Корені відповідних рівнянь попарно рівні:
x1=x3=5, x2=6 і x4=4.
Сукупність нерівностей означає, що розв'язки обох нерівностей будемо об'єднувати, графічно це має вигляд
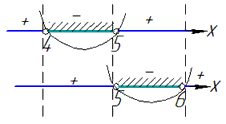
або інтервальний запис x∈(4;5)∪(5;6).
Відповідь: (4;5)∪(5;6). – А.
Приклад 11.20 Знайти множину розв'язків нерівності 7/(|x|+5)<1.

Обчислення: Дробову нерівність з модулем
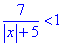
за правилами розкриття модулів замінюємо еквівалентною системою.
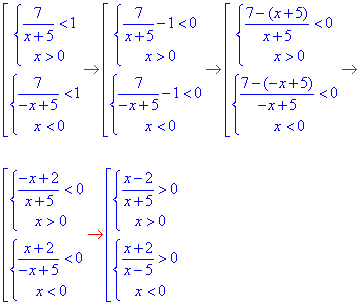
Після спрощення дробів отримаємо строгі нерівності, які замінюємо квадратичними нерівностями з додатковими умовами
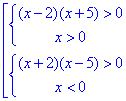
перша нерівність справедлива при додатних значеннях "ікса", а друга – від'ємні.
На числових осях отримаємо наступні області
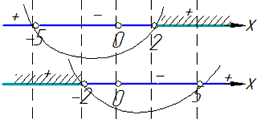
В результаті об'єднання отримаємо два інтервали x∈(-∞;-2)∪(2;+∞).
Відповідь: (-∞;-2)∪(2;+∞). – В.
Приклад 11.21 Знайти множину розв'язків нерівності (x+2)(x-a)/(x-4)≤0, якщо значення параметра лежать в межах -2<a<3.
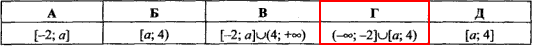
Обчислення: Обчислення дробових нерівностей з параметром вимагає більшої уваги, аніж простих, тому все що написано далі уважно перегляньте та застосовуйте на практиці.
Задана нерівність з параметром
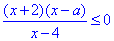
нестрога і за правилами ми можемо її замінити еквівалентною системою нерівностей:
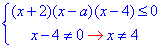
Відповідне рівняння має вигляд
(x+2)(x-a)(x-4)=0, звідси x1=-2, x2=a (якщо -2<a<3) і x3=4.
Тут завжди слідкуйте за тим, який з інтервалів розбивається параметром на два. Наносимо їх на числову вісь і методом підстановки визначаємо знаки.

Отримаємо два інтервали x∈(-∞;-2]∪[a;4).
Відповідь: (-∞;-2]∪[a;4) – Г.
Приклад 11.22 Знайти множину розв'язків нерівності
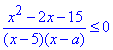
якщо параметр обмежений числами -3<a<5.

Обчислення: Схема обчислень незмінна від завдання до завдання.
Спершу дробову нерівність замінюємо еквівалентною системою:
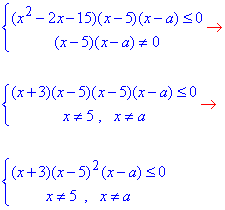
Після розкладу квадратичної залежності на прості множники, виписуємо рівння:
(x+3)(x-5)^2(x-a)=0, та знаходимо нулі x1=-3, x2=a (якщо -3<a<5) і x3=5.
Як бачимо, вираз (x-5)^2 має парну степінь, тому крива свій знак змінювати не буде при проходженні через точку x=5.
Отримали один інтервал x∈(-3;a), який відповідає варіанту Б ЗНО тестів.
Відповідь: Б.
Приклад 11.23 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А – Д).

Обчислення: Почергово розв'язуємо завдання та співставляємо отримані відповіді до нерівностей з тестовими.
1) Зводимо до різниці квадратів

звідси маємо два корені x1=-√3 і x2=√3.
Наносимо їх на числову вісь, а далі підстановкою нуля перевіряємо знаки.
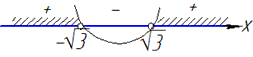
На основі рисунку виписуємо множину розв'язків нерівності
x∈(-∞;-√3)∪(√3;+∞) - Д;
2) Розкриваємо модуль |x|≤√3 та замінюємо нерівність
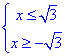
Корені зображуємо на числовій осі, та заштриховуємо потрібні
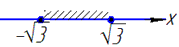
отримали інтервал x∈(-√3;√3) - В;
3) Записуємо рівносильну нерівність
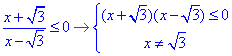
Далі знаходимо нулі x1=-√3 і x2=√3, та розв'язки x∈(-√3;√3) - А;

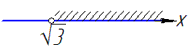
4) x-√3>0, звідси x>√3, тобто x∈(√3;+∞) - Г.
Приклад 11.24 Установити відповідність між нерівностями (1–4) та рівносильними їм нерівностями (А – Д).
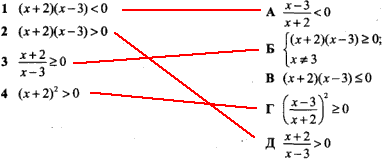
Обчислення: В попередніх нерівностях постійно замінювали дробові нерівності рівносильними квадратичними чи вищого степеня, тому тут лише застосуємо попередньо подані методи розв'язування нерівностей, які були використані раніше.
Не вдаючись в деталі, записуємо відповіді:
1 – А, 2 – Д, 3 – Б, 4 – Г.
Ще 10 готових відповідей до тестових дробових нерівностей розглянемо в наступних публікаціях.



