В данном уроке будут рассмотрены интегралы вида R(sin(x),cos(x))
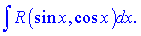
Такая запись указывает на то, что над синусом и косинусом проводятся исключительно рациональные операции: сложение и вычитание, умножение на константы, возведение к целому степени, деление. Проще говоря, подынтегральная функция - это рациональная функция от синуса и косинуса.
Такие интегралы сводятся к интегралам от рациональной функции нового аргумента 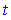 подстановкой, которую еще называют универсальной:
подстановкой, которую еще называют универсальной:
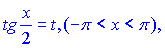
тогда
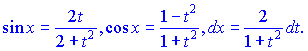
Бывают примеры, когда приведенная подстановка приводит к сложным интегралам. Поэтому для ряда случаев, в силу четности или нечетности подынтегральной функции, существуют более простые подстановки:
а) 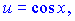 если
если 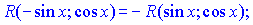
б) 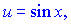 если
если 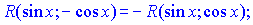
в) 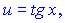 если
если 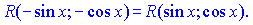
Пример 1.
Вычислить интегралы
а) 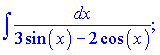
б) 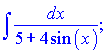
в) 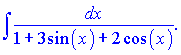
Решение.
а) Применим тригонометрическую подстановку
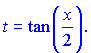
На ее основе получим
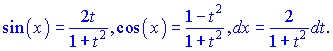
Подставим в интеграл и проинтегрируем
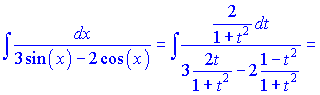
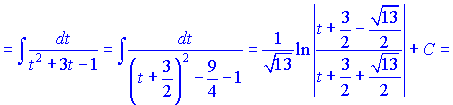
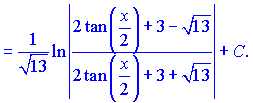
б) К данному примеру применяем нужную замену
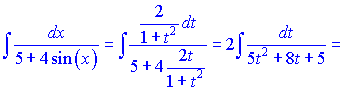
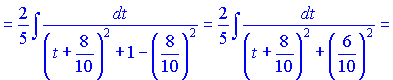
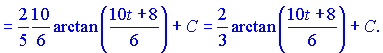
в) Применяем замену из примера б)
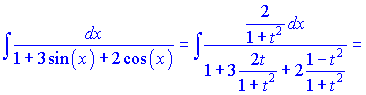
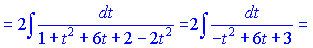
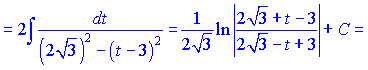
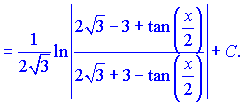
-------------------------------------------
Интегрирование рациональных функций от sin(x),cos(x) довольно сложное, поэтому следует бить внимательными при упрощении подынтегральной функции, а также при самом интегрировании. Самая малая опечатка может привести к неправильному результату, не торопитесь вычисляя подобные интегралы.


