Серед простих формул інтегрування відсутні готові залежності, які б дозволяли знайти інтеграл від тангенса (tg(x)) та котангенса (ctg(x)). Але такі приклади в завданнях зустрічаються і потрібно знати, як обчислити інтеграл від тангенса та котангенса. Почнемо з тангенса, розпишемо його у вигляді частки синуса на косинус
tg(x)=sin(x)/cos(x)
та підставимо в інтеграл.
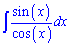Наразі все Вам зрозуміло. Далі потрібно внести синус під диференціал, щоб звести інтегрування до логарифма
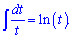В результаті отримаємо
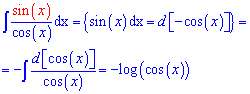Таким чином вивели просту і потрібну на практиці формулу - інтеграл від тангенса рівний логарифму косинуса зі знаком мінус.
Int(tan(x),x)=-log(cos(x)).
За наведеною схемою виведемо формулу для інтегралу від котангенса. Записуємо частку косинуса на синус в інтеграл та після внесення косинуса під диференціал зводимо інтеграл до логарифма
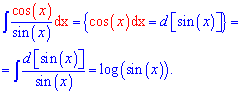Інтеграл від котангенса рівний логарифму від синуса.
Int(cot(x),x)=log(sin(x)).
Прості на вигляд формули інтегралів від тангенса та котангенса дозволяють розв'язати чимало складніших прикладів, як наприклад інтегрування тангенса подвійного кута чи котангенса половини кута.
Приклади інтегрування тангенса та котангенса
Приклад 1. Знайти інтеграл від тангенса tan(4*x).
Обчислення: Застосовуємо наведену вище методику для інтегрування тангенса
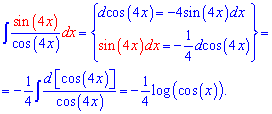
Тут в дужках ми спершу обчислюємо диференціал від косинуса, а далі виділяємо значення, яке нам потрібно дістати. Далі інтегрування зводимо до логарифма.
Таким чином можемо записати узагальнену формулу для інтегралу від
tan(k*x) Int(tan(k*x),x)=-1/k*(log(cos(x)).
За цією формулою інтеграл від тангенса подвійного кута рівний логарифму косинуса подвійного кута помноженому на -0,5.
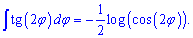Для тангенса половини кута tan(phi/2) інтеграл рівний -2 помножити на логарифм косинуса половини кута
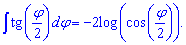По індукції отримаємо формулу інтеграла для тангенса третини кута tan(phi/3)
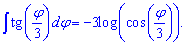
Приклад 2. Проінтегрувати котангенс подвійного кута.
Обчислення: По аналогії з формулами для тангенса ми могли б виписати готову формулу, але краще виконати проміжні переходи, щоб Ви краще зрозуміли і завчили метод внесення під диференціал
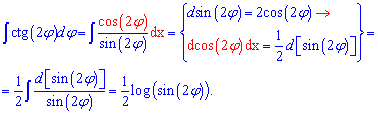
Таким чином, якщо маємо котангенс потрійного кута то перед інтегралом отримаємо множником 1/3
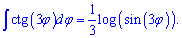Інтеграли від котангенса половини та третини кута будуть мати множниками перед логарифмом відповідно двійку та трійку
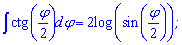
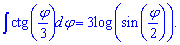При знаходженні первісної від тангенса та котангенса слід справа додати сталу
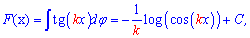
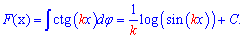Знаючи дану методику, ви знаєте як знайти інтеграл від тангенса, аргумент якого містить множником довільне число.
Обчислення означених інтегралів від тангенса та котангенса в даній статті розглядати не будемо. Якщо Ви обчислювали такі інтеграли від простих функцій то знаючи синуси та косинуси кутів знайти визначений інтеграл від тангенса чи котангенса зможете без проблем.
З методикою інтегрування обернених тригонометричних функцій, ірраціональних та показникових Ви можете ознайомитися на сторінках категорії "Інтегрування функції" в правому меню сайту.
