Розберемо ще три готові відповіді до задач на відстані між площинами, точками і прямими. Від Вас потрібні добрі знання трикутників, теореми синусів та Піфагора. Пояснення добре обгрунтовані та повинні бути легкими для сприйняття школярами 10-11 класів.
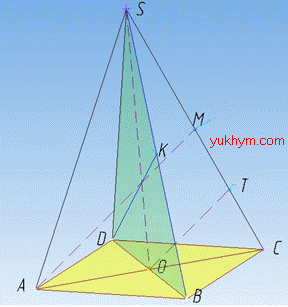
Задача 35.26 На рисунку зображено правильну чотирикутну піраміду SABCD, у якої SO – висота, M – середина ребра SC, діагональні перерізи – рівносторонні трикутники.
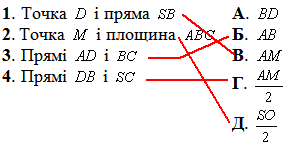
Установити відповідність між точками, прямими, площинами (1–4) та відстанями між ними (А–Д).
Розв'язання: 1) За умовою задачі, SABCD – правильна чотирикутна піраміда, діагональні перерізи – рівносторонні трикутники, тому трикутники ASC і BCD рівні. Це означає, що їх відповідні висоти, медіани і бісектриси також рівні.
Нехай точка K – середина ребра SB, тоді DK – медіана (і одночасно висота) рівностороннього ΔBSD, тобто DK⊥SB. З цього слідує, що відрізок DK – відстань від точки D до прямої SB. Відрізок DK дорівнює відрізку AM (DK=AM), оскільки за умовою задачі, точка M – середина ребра SX, і рівносторонні трикутники ASC і BCD рівні. Тому відстань від точки D до прямої SB дорівнює довжині відрізка A.
1 – В.
2) З точки M на площину ABC опустимо перпендикуляр MN. Точка N належить площині ABC. Розглянемо площину (трикутник) SOC. Оскільки дві прямі MH і SO перпендикулярні до площини ABC (SO – висота піраміди SABCD), то за властивістю, прямі MH і SO паралельні (MH||SO). За умовою задачі, точка M – середина ребра SC, звідси слідує, що MH – середня лінія трикутника SOC. За властивістю середньої лінії, MH=SO/2. Отже, відстань від точки M до площини ABC дорівнює SO/2 (половині висоти SO піраміди SABCD).
2 – Д.
3) В основі піраміди SABCD лежить правильний чотирикутник, тобто квадрат ABCD. У квадрата сусідні сторони перпендикулярні, а протилежні сторони паралельні (за означенням).
Відстань між прямими AD і BC – це їх спільний перпендикуляр, тобто AD⊥AB і BC⊥AB. Отже, відстань між прямими AD і BC є довжина відрізка AB.
3 – Б.
4) З точки O паралельно відрізку AM проведемо відрізок OT, де точка T належить ребру SC. Оскільки DB⊥OC (ABCD – квадрат), то за теоремою про три перпендикуляри (дивись задачу 35.18) DB⊥OT.
Так як AM⊥SC (AM – висота ΔASC) і AM||OT за побудовою, то, за властивістю прямих у просторі, OT⊥SC.
Відстань між прямими DB і SC – це спільний перпендикуляр OT, який є середньою лінією трикутника AMC, оскільки точка O – середина AC і AM||OT. Тому, за властивістю середньої лінії трикутника, OT=AM/2.
Отже, відстань між прямими DB і SC є половина довжини відрізка AM , тобто дорівнює AM/2.
4 – Г.
Задача 35.34 Один з катетів прямокутного трикутника ABC дорівнює 6, а гострий кут, прилеглий до цього катета, дорівнює 300. Через вершину прямого кута C проведено відрізок CD, перпендикулярний до площини цього трикутника, CD=4. Визначити відстань від точки D до прямої AB.
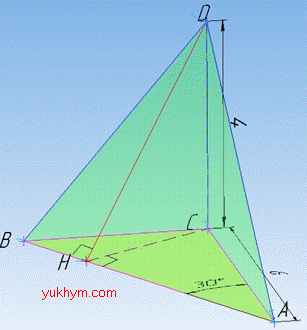
Розв'язання: За умовою задачі маємо прямокутний трикутник (площину) ABC (∠ACB=90, тобто AC⊥BC), у якого AC=6 – катет, ∠BAC=30 – гострий кут, прилеглий до катета AC. Точка D не лежить в площині ABC за умовою задачі. З точки D опустимо перпендикуляр CD=4 – відстань від точки D до площини трикутника ABC, тобто CD⊥(ABC).
Відстань від точки D до прямої AB – перпендикуляр DH, опущений з точки D на пряму AB, де точка H належить прямій AB, тобто DH⊥AB.
Проведемо відрізок CH, якій належить площині ABC. Оскільки CD⊥(ABC), то CD⊥CH, тобто CD – перпендикуляр і DH – похила, проведені до площини трикутника ABC, а CH – проекція похилої DH на площину трикутника ABC.
Оскільки DH⊥AB, то за теоремою «про три перпендикуляри» CH⊥AB. Звідси слідує, що CH – висота прямокутного трикутника ABC проведена до гіпотенузи AB. Розглянемо прямокутний трикутник ACH (∠AHC=90), у якого AC=6 – гіпотенуза, ∠HAC=30 – гострий кут, протилежний до катета CH. За означенням синуса гострого кута прямокутного трикутника знайдемо довжину катета CH:
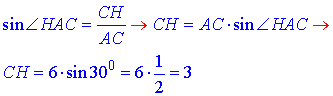
Розглянемо прямокутний трикутник DCH (∠DCH=90), у якого CD=4 і CH=3 – катети. За теоремою Піфагора знайдемо довжину гіпотенузи DH – відстань від точки D до сторони AB:
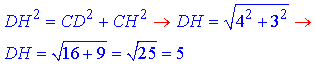
Відповідь: 5.
Задача 35.35 З точки A, що розміщена на колі, радіус якого 2, побудований перпендикуляр AK завдовжки 1 до площини круга. З точки a проведено діаметр AB, а з точки B під кутом 450 до діаметра – хорду BC. Знайти у сантиметрах відстань від точки K до хорди BC.
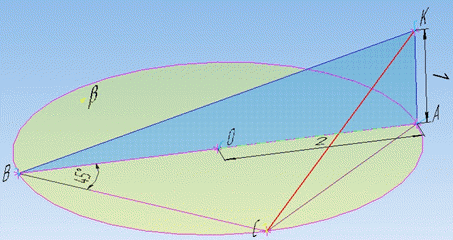
Розв'язання: За умовою задачі маємо: площину beta – коло з центром в точці O і радіусом R=2;
точку A, що лежить на колі;
AB=4 – діаметр кола;
BC – хорда кола, ∠ABC=45.
В площині beta (на колі) проведемо відрізок (хорду) AC.
Оскільки, за властивістю кут, який спирається на діаметр – прямий, то ∠ACB=90.
Звідси, ΔABC – прямокутний з гіпотенузою AB=4, гострим кутом ∠ABC=45. Точка K не лежить в площині beta за умовою задачі. З точки K опустимо перпендикуляр AK=1 – відстань від точки K до площини кола, тобто AK⊥beta, звідси AK⊥AB і AK⊥AC.
Проведемо відрізок KC. Оскільки AC⊥BC, то за теоремою «про три перпендикуляри» KC⊥BC. Тому відстань від точки K до хорди BC – перпендикуляр CK, опущений з точки K на пряму BC.
Розглянемо прямокутний трикутник ABC (∠ACB=90), у якого AB=4 – гіпотенуза, ∠ABC=45 – гострий кут, протилежний до катета AC.
За означенням синуса гострого кута прямокутного трикутника знайдемо довжину катета AC:
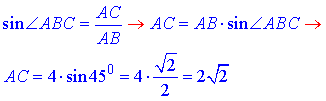
Розглянемо прямокутний трикутник AKC (∠KAC=90), у якого AK=1 і  – катети.
– катети.
За теоремою Піфагора знайдемо довжину гіпотенузи KC – відстань від точки K до сторони BC:
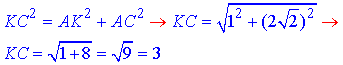
Відповідь: 3.


