ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 110. Знайдіть проміжки зростання і спадання та точки екстремуму функції:
1) 
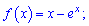
Розв'язання.
Похідну функції
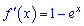
прирівнюємо до нуля
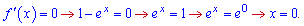
Встановлюємо знак похідної підстановкою точки, наприклад 1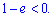 
Похідна змінює знак з додатного на від'ємний, отже в точці x=0 функція приймає максимальне значення
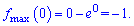
Отже (0;1) – точка максимуму. Перед нею функція зростає
,
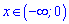а за нею спадає
.
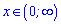2) 
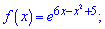
Розв'язання.
Похідну від експоненти прирівнюємо до нуля і визначаємо точки підозрілі на екстремум
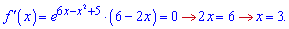
Для перевірки знаку підставимо нуль
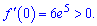
Отже в знайденій точці функція приймає максимум
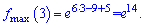
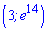– точка максимуму.
На інтервалі
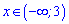
функція зростає, а далі спадає
.
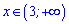3) 
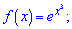
Розв'язання.
Похідна функції
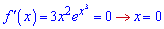
є додатною на всій дійсній осі, а тому функція постійно зростає.
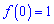
Точка (0;1) не є екстремальною.
4) 
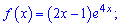
Розв'язання.
Похідну функції прирівнюємо до нуля
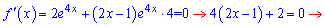
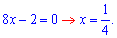
Похідна в нулі від'ємна
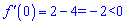
отже знайдена точка є мінімальною. Значення функції в точці мінімуму рівне
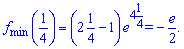
Функція спадає зліва від точки
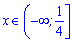
і зростає справа
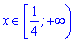
5) 
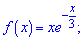
Розв'язання.
Обчислимо похідну
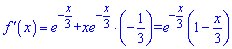
Знайдемо критичну точку
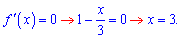
В нулі похідна більша за нуль, отже зліва функція зростає – значить маємо максимум.
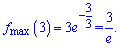
Функція зростає, якщо змінна належить інтервалу
,
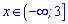спадає на його продовженні
.
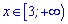6) 
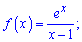
Розв'язання.
Область визначення – вся дійсна вісь крім одиниці (знаменник рівний нулю). Знаходимо похідну від частки
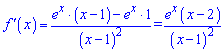
і критичну точку
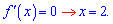
В точці x=3 похідна додатна, лівіше від'ємна. При переході через одиницю похідна не змінює знак, оскільки знаменнику дужка в парному степені. В точці x=2 функція приймає мінімальне значення
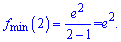
Функція спадає на інтервалах
,
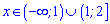зростає при змінній рівній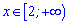 
.
7) 
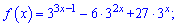
Розв'язання.
Обчислюємо похідну від показникового рівняння
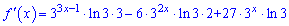
Знаходимо точки підозрілі на екстремум
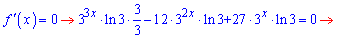
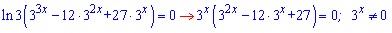
Вводимо заміну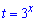 
та розв'язуємо отримане квадратне рівняння
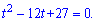
Коренями будуть t=3;t=9. Встановлюємо знак підстановкою нуля в похідну
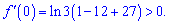
Повертаємося до заміни
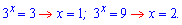
Отже між коренями функція спадає
,
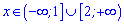а поза ними зростає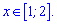 
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Похідна показникової та логарифмічної функцій. №107-109
- Наступні відповіді - Похідна показникової та логарифмічної функцій. №110 (8-12)
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!
